3D Vectors
3D Vectors Revision
3D Vectors
Working with 3D vectors is mostly similar to 2D vectors, however the calculations can be more complicated.
3D vectors introduces another unit vector, \boldsymbol{\textcolor{blue}{k}}, which corresponds to the \textcolor{blue}{z}-axis.
Make sure you are happy with the following topics before continuing.
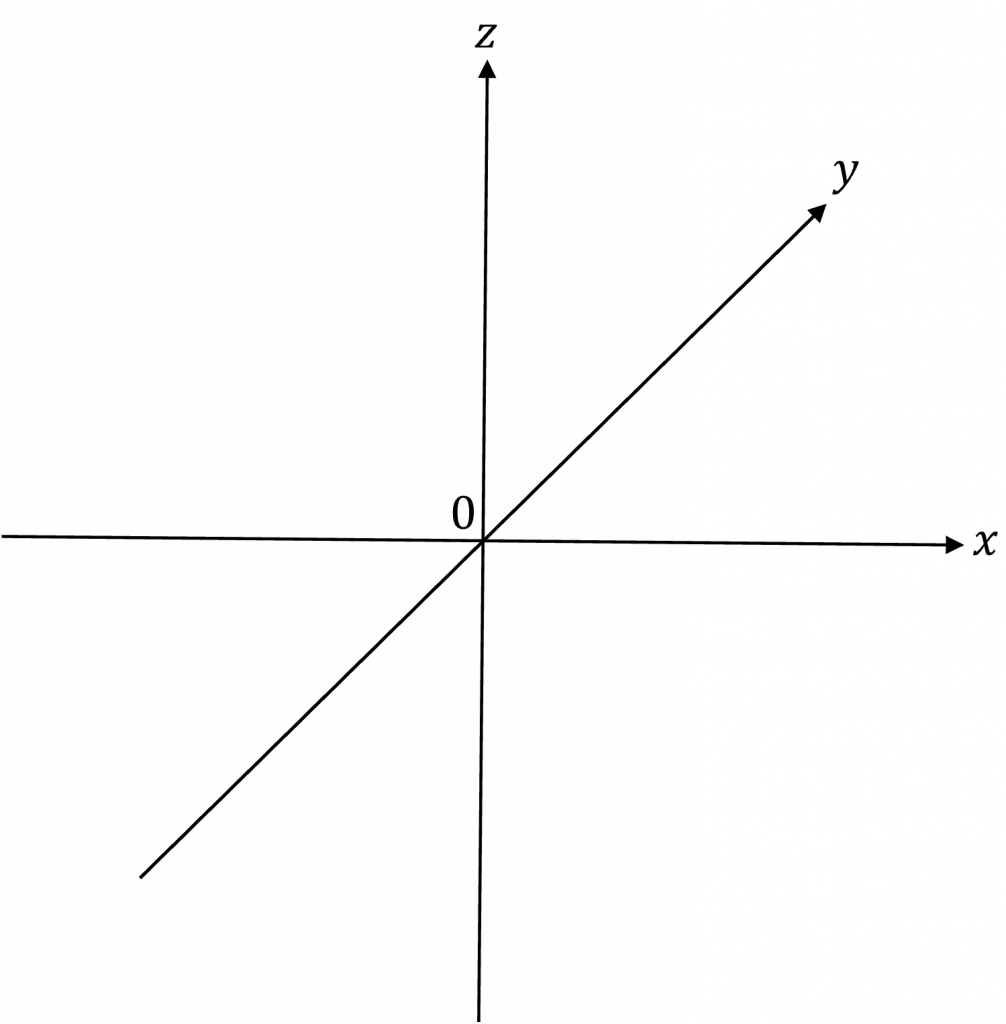

Unit Vectors in Three Dimensions
Three dimensions inevitably introduces a third axis, the z-axis. We can visualise the z axis by imagining that the x-axis and y-axis lie flat on a surface and then the z-axis points upwards, as shown by the diagram on the right.
When working with vectors \boldsymbol{k} is the unit vector in the direction of the z-axis.
Three dimensional vectors follow the same form as two dimensional vectors, they are written as: x\boldsymbol{i}+y\boldsymbol{j}+z\boldsymbol{k}=\begin{pmatrix} x \\ y \\ z \end{pmatrix}
Addition, subtraction, multiplying with scalars and showing two vectors are parallel (Vector Basics) all work the same with 3D vectors as with 2D vectors.
Pythagoras in Three Dimensions
To find the distance of any 3D point from the origin we can use a variation of Pythagoras’ theorem:
Distance of point (x,y,z) from the origin =\sqrt{x^2+y^2+z^2}
Therefore, finding the magnitude of any 3D vector can be found in the same way as finding the magnitude of a 2D vector.
Example:
Find the magnitude of the vector \boldsymbol{s}=3\boldsymbol{i}-5\boldsymbol{j}+2\boldsymbol{k} to 2 decimal places.
|\boldsymbol{s}|=\sqrt{3^2+(-5)^2+2^2}=\sqrt{38}=6.16 units (2\text{ dp})
We can also use a Pythagoras-based formula to find the distance between two points in three dimensions:
Distance between points (x_{1}, y_{1}, z_{1}) and (x_{2}, y_{2}, z_{2}) is \sqrt{(x_{1}-x_{2})^2 +(y_{1}-y_{2})^2 +(z_{1}-z_{2})^2}
Example:
The position vector of point O is \begin{pmatrix} 4 \\ 6 \\ -3 \end{pmatrix} and the position vector of point P is \begin{pmatrix} 1 \\ -5 \\ 4 \end{pmatrix}.
Find |\overrightarrow{OP}| to 2 decimal places.
|\overrightarrow{OP}|=\sqrt{(4-1)^2+(6-(-5))^2+((-3)-4)^2}=\sqrt{9+121+49}=13.38 units (2 \text{ dp})
Example: Problems in 3D
Point A has a position vector of -4\boldsymbol{i}+3\boldsymbol{j}+6\boldsymbol{k} and point B has a position vector of 2\boldsymbol{i}-5\boldsymbol{j}+3\boldsymbol{k}. Point C lies on the vector line AB and divides the line in the ratio 4:3. Find the position vector of C.
It is often helpful to split 3D problems into multiple parts and draw 2D diagrams to help you visualise them.
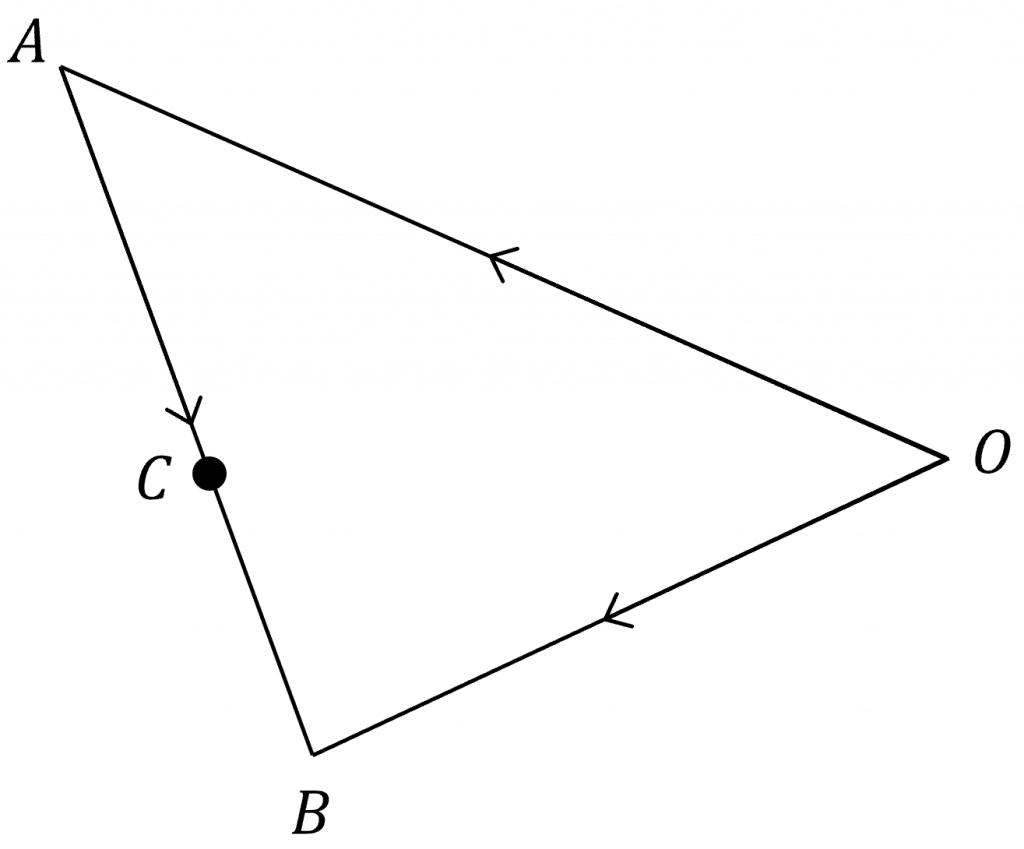

1) We first need to find the vector \overrightarrow{AB}:
\begin{aligned} \overrightarrow{AB} &= \overrightarrow{OB}-\overrightarrow{OA} \\ &= (2-(-4))\boldsymbol{i}+(-5-3)\boldsymbol{j}+(3-6)\boldsymbol{k} \\ &=6\boldsymbol{i}-8\boldsymbol{j}-3\boldsymbol{k} \end{aligned}2) We are told that C divides \overrightarrow{AB} in the ratio 4:3, so C is \dfrac{4}{7} of the way along \overrightarrow{AB}.
Thus, \overrightarrow{AC}=\dfrac{4}{7}\overrightarrow{AB}=\dfrac{4}{7}(6\boldsymbol{i}-8\boldsymbol{j}-3\boldsymbol{k})=\dfrac{24}{7}\boldsymbol{i}-\dfrac{32}{7}\boldsymbol{j}-\dfrac{12}{7}\boldsymbol{k}
3) Finally, to find the position vector of C we need to add the vector \overrightarrow{AC} to \overrightarrow{OA}.
\begin{aligned} \overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{AC} &=(-4\boldsymbol{i}+3\boldsymbol{j}+6\boldsymbol{k})+(\dfrac{24}{7}\boldsymbol{i}-\dfrac{32}{7}\boldsymbol{j}-\dfrac{12}{7}\boldsymbol{k}) \\ &= -\dfrac{4}{7}\boldsymbol{i}-\dfrac{11}{7}\boldsymbol{j}+\dfrac{30}{7}\boldsymbol{k} \end{aligned}3D Vectors Example Questions
Question 1: Find the magnitudes of the following vectors, give your answer to 2 decimal places.
a) \overrightarrow{OA}=5\boldsymbol{i}-2\boldsymbol{j}+\boldsymbol{k}
b) \overrightarrow{OB}=-2\boldsymbol{i}-6\boldsymbol{j}+7\boldsymbol{k}
c) \overrightarrow{OC}=\begin{pmatrix} 4 \\ 9 \\ -3 \end{pmatrix}
[3 marks]
Using a variation of Pythagoras’ theorem:
a) |\overrightarrow{OA}|=\sqrt{5^2+(-2)^2+1^2}=\sqrt{30}=5.48 units (2 \text{ dp})
b) |\overrightarrow{OB}|=\sqrt{(-2)^2+(-6)^2+7^2}=\sqrt{89}=9.43 units (2 \text{ dp})
c) |\overrightarrow{OC}|=\sqrt{4^2+9^2+(-3)^2}=\sqrt{106}=10.30 units (2 \text{ dp})
Question 2:
\boldsymbol{x}=3\boldsymbol{i}+8\boldsymbol{j}-4\boldsymbol{k}
\boldsymbol{y}=-2\boldsymbol{i}-7\boldsymbol{j}-\boldsymbol{k}
\boldsymbol{z}=6\boldsymbol{i}+9\boldsymbol{j}+3\boldsymbol{k}
Find 3\boldsymbol{y}+2\boldsymbol{z}-\boldsymbol{x}
[2 marks]
Question 3: Points L, M and N have position vectors \begin{pmatrix} 1 \\ 5 \\ -2 \end{pmatrix}, \begin{pmatrix} 3 \\ -3 \\ -1 \end{pmatrix} and \begin{pmatrix} 5 \\ 7 \\ -5 \end{pmatrix} respectively.
Show that \overrightarrow{OL} is parallel to \overrightarrow{MN}.
[2 marks]
We need to first find \overrightarrow{MN}:
\overrightarrow{MN}=\overrightarrow{ON}-\overrightarrow{OM}=\begin{pmatrix} 5 \\ 7 \\ -5 \end{pmatrix}-\begin{pmatrix} 3 \\ -3 \\ -1 \end{pmatrix}=\begin{pmatrix} 2 \\ 10 \\ -4 \end{pmatrix}
We can see that \begin{pmatrix} 2 \\ 10 \\ -4 \end{pmatrix} \times \dfrac{1}{2}=\begin{pmatrix} 1 \\ 5 \\ -2 \end{pmatrix}
Thus, 2\overrightarrow{OL}=\overrightarrow{MN}, so \overrightarrow{OL} is parallel to \overrightarrow{MN} because they are scalar multiples of each other.
Question 4: Point A has a position vector of 2\boldsymbol{i}-6\boldsymbol{j}+5\boldsymbol{k} and point B has a position vector of \boldsymbol{i}-4\boldsymbol{j}-3\boldsymbol{k}.
The point X lies on the line AB and divides the line in the ratio 3:1.
Calculate the distance of X from the origin, giving your answer to 2 decimal places.
[4 marks]
First, we need to find the position vector of \overrightarrow{AB}:
\overrightarrow{AB}=\overrightarrow{OB}-\overrightarrow{OA}=(\boldsymbol{i}-4\boldsymbol{j}-3\boldsymbol{k})-(2\boldsymbol{i}-6\boldsymbol{j}+5\boldsymbol{k})=-\boldsymbol{i}+2\boldsymbol{j}-8\boldsymbol{k}
We know that the point X divides the line AB in the ratio 3:1, so \overrightarrow{AX}=\dfrac{3}{4}\overrightarrow{AB}=-\dfrac{3}{4}\boldsymbol{i}+\dfrac{3}{2}\boldsymbol{j}-6\boldsymbol{k}
Then to find the distance between the point X and the origin, we need to find the position vector of \overrightarrow{OX}:
\begin{aligned}\overrightarrow{OX}=\overrightarrow{OA}+\overrightarrow{AX} &= (2\boldsymbol{i}-6\boldsymbol{j}+5\boldsymbol{k})+(-\dfrac{3}{4}\boldsymbol{i}+\dfrac{3}{2}\boldsymbol{j}-6\boldsymbol{k}) \\ &=\dfrac{5}{4}\boldsymbol{i}-\dfrac{9}{2}\boldsymbol{j}-\boldsymbol{k} \end{aligned}
Finally, |\overrightarrow{OX}|=\sqrt{(\dfrac{5}{4})^2+(-\dfrac{9}{2})^2+(-1)^2}=4.78 units (2 \text{ dp})
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.







