Arc Length & Area of a Sector
Arc Length & Area of a Sector Revision
Arc Length & Area of a Sector
We’ll now look at how to calculate arc lengths and sector areas.
Make sure you’re up to snuff on your radians!
Arc Length
Let’s say you’ve got a section of a circle, and you want to find the length of the curved edge.
For a circle with radius \textcolor{red}{r} and angle \textcolor{blue}{\theta}, we have the arc length \textcolor{purple}{l} = \textcolor{red}{r}\textcolor{blue}{\theta}.
As mentioned, it’s important that you’re using radians for your value of \textcolor{blue}{\theta}.
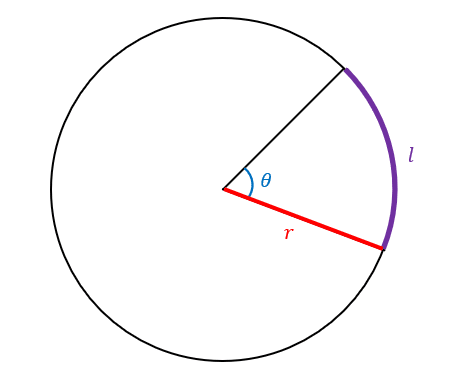
We can actually use this formula to derive the circumference of a circle.
Set \textcolor{blue}{\theta} = 2\pi. Then we have \textcolor{purple}{l} = 2\textcolor{red}{r}\pi = d\pi, where d is the diameter.
A Level Maths Predicted Papers 2024
The MME A level maths predicted papers are an excellent way to practise, using authentic exam style questions that are unique to our papers. Our examiners have studied A level maths past papers to develop predicted A level maths exam questions in an authentic exam format. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
A Level Maths Revision Cards
The best A level maths revision cards for AQA, Edexcel, OCR, MEI and WJEC. MME is here to help you prepare effectively for your A Level maths exams. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
Area of a Sector
Say we have the same section of a circle, but we now wish to calculate the area of the sector.
For a circle with radius \textcolor{red}{r} and angle \textcolor{blue}{\theta}, we have the sector area \textcolor{orange}{A} = \dfrac{1}{2}\textcolor{red}{r}^2\textcolor{blue}{\theta}.
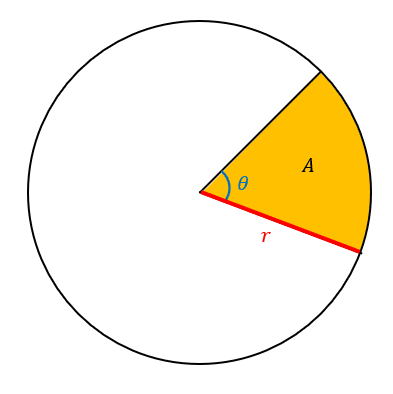
Again, using \textcolor{blue}{\theta = 2\pi} gives us the equation for the area of a circle:
\textcolor{orange}{A} = \dfrac{1}{2}\textcolor{red}{r}^2 \textcolor{blue}{2\pi} = \pi \textcolor{red}{r}^2.
Example 1: Arc Length
The following circle has radius \textcolor{red}{r} = \textcolor{red}{5}\text{ cm} and angle \textcolor{blue}{\theta} = \textcolor{blue}{105}\degree.
By converting the angle into radians, find the length of \textcolor{purple}{l} to 2 decimal places.
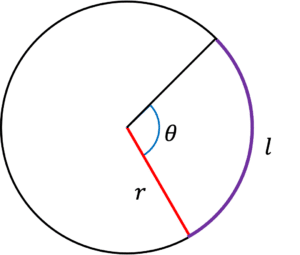
[3 marks]
To convert degrees to radians, we multiply \textcolor{blue}{\theta} by \dfrac{\pi}{180}\\
\textcolor{blue}{105}\degree\times\dfrac{\pi}{180}=\textcolor{blue}{\dfrac{7\pi}{12}}\\
Now we can use this formula to calculate the arc length:
\textcolor{purple}{l} = \textcolor{red}{r}\textcolor{blue}{\theta}\\ \textcolor{purple}{l} = \textcolor{red}{5}\times\textcolor{blue}{\dfrac{7\pi}{12}}\\ \textcolor{purple}{l} = 9.16\text{ cm}\\
Example 2: Area of a Sector
The following circle has radius \textcolor{red}{r} = \textcolor{red}{4}\text{ cm} and angle \textcolor{blue}{\theta} = \textcolor{blue}{\dfrac{5\pi}{6}}\text{ radians}.
Find the area of the shaded sector to 2 decimal places.
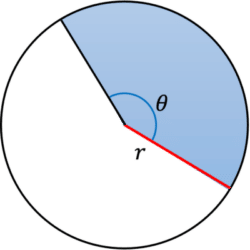
[2 marks]
As the angle is in radians, we can use this formula to calculate the area of the sector:
Area = \dfrac{1}{2}\textcolor{red}{r}^2\textcolor{blue}{\theta}\\
Area = \dfrac{1}{2}\times\textcolor{red}{4}^2\times\textcolor{blue}{\dfrac{5\pi}{6}}\\
Area = 20.94\text{ cm}^2\\
Arc Length & Area of a Sector Example Questions
Question 1: What is the perimeter of a section of a circle with angle \theta = 45° and radius r = 9\text{ mm}? Give your answer in the form 9(a + b\pi).
[3 marks]
Firstly, we have
\theta = 45° = \dfrac{\pi}{4}
Then the length of the arc is
l = r\theta = \dfrac{9\pi}{4}
Giving the total perimeter
\dfrac{9\pi}{4} + 9 + 9 = 9(2 + \dfrac{\pi}{4})\text{ mm}
Question 2: A spinner of radius 4\text{ cm} has 6 identical sections. Using the equation for sector area, find the shaded area (in \text{cm}^2).
[2 marks]
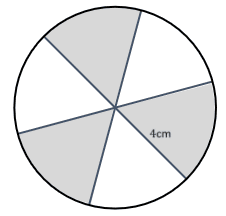
First of all, the angle \theta = 60° = \dfrac{\pi}{3}.
The area of one sector is
\dfrac{1}{2}r^2 \theta = \dfrac{1}{2} \times 4^2 \times \dfrac{\pi}{3} = \dfrac{8\pi}{3}\text{ cm}^2
so the area of all three identical sectors is 8\pi\text{ cm}^2.
Question 3: Here is a plot for a garden, including a pool and a patio (grey). Find the area of the garden covered by grass, in the form a + b\pi.
[4 marks]
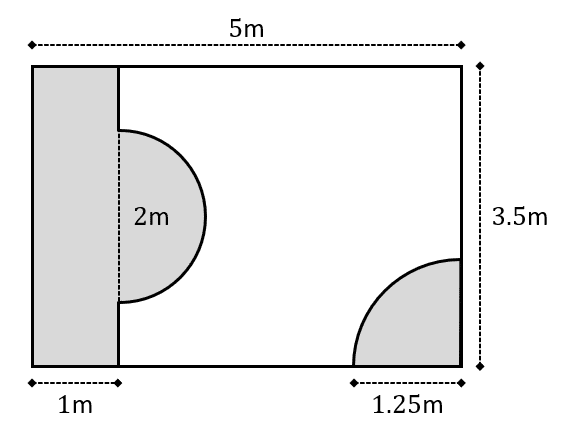
Total area of garden:
5 \times 3.5 = 17.5
Area of patio:
(1 \times 3.5) + (\dfrac{1}{2} \times 1^2 \times \pi) = 3.5 + \dfrac{\pi}{2}
Area of pool:
\dfrac{1}{2} \times 1.25^2 \times \dfrac{\pi}{2} = \dfrac{25\pi}{64}
Then, the total area covered by grass is
17.5 - (3.5 + \dfrac{\pi}{2} + \dfrac{25\pi}{64}) = 14 - \dfrac{57}{64}\pi
You May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.
