Cubics
Cubics Revision
Cubics
A cubic is an expression in the form \textcolor{red}{a}x^3 + \textcolor{blue}{b}x^2 + \textcolor{limegreen}{c}x + \textcolor{orange}{d}. You can factorise cubics, in a similar way to factorising quadratics – however it it a little trickier. There are 2 methods used to factorise cubics.
Make sure you are happy with the following topics before continuing.
Method 1: Factorising Cubics given 1 Factor
When factorising a cubic expression, you will be able to put it into (up to) 3 brackets. You may be given 1 factor that you can work with, which will make the factorisation easier.
Example: (x-2) is a factor of f(x) = 2x^3 + x^2 - 13x + 6. Hence, express f(x) as a product of three linear factors.
Step 1: Write down the factor we know, \textcolor{orange}{(x-2)}, next to another set of brackets:
\textcolor{orange}{(x-2)}( \quad \quad \quad \quad \quad \quad ) = 2x^3 + x^2 - 13x + 6
Step 2: Put an x^2 term at the start of the second set of brackets – this will need to multiply together with x from the first bracket to make 2x^3:
\textcolor{orange}{(x-2)}(\textcolor{red}{2x^2} \quad \quad \quad \quad ) = 2x^3 + x^2 - 13x + 6
Step 3: Find the constant term for the end of the second bracket – this will need to be multiplied together with -2 to make 6:
\textcolor{orange}{(x-2)}(\textcolor{red}{2x^2} \quad \quad \quad \textcolor{limegreen}{-3}) = 2x^3 + x^2 - 13x + 6
Step 4: The x and -3 above multiply to make -3x, but we need -13x. So we need an extra -10x from somewhere – we need to multiply -2 by 5x to make -10x:
\textcolor{orange}{(x-2)}(\textcolor{red}{2x^2} + \textcolor{blue}{5x} \textcolor{limegreen}{-3}) = 2x^3 + x^2 - 13x + 6
Step 5: Check that this works, by multiplying out the brackets and seeing if this matches f(x):
\begin{aligned} &\, \textcolor{orange}{(x-2)}(\textcolor{red}{2x^2} + \textcolor{blue}{5x} \textcolor{limegreen}{-3}) \\ &= 2x^3 + 5x^2 - 3x - 4x^2 - 10x + 6 \\ &= 2x^3 + x^2 - 13x + 6 \end{aligned}
So, this works so far.
Step 6: Factorise the quadratic 2x^2 + 5x -3 into 2 linear factors:
\textcolor{red}{2x^2} + \textcolor{blue}{5x} \textcolor{limegreen}{-3} = \textcolor{orange}{(2x-1)(x+3)}
Step 7: Put it all together:
2x^3 + x^2 - 13x + 6 = \textcolor{orange}{(x-2)(2x-1)(x+3)}
Method 2: Factorising Cubics using the Factor Theorem
If you are given no factors, then you can use the Factor Theorem to find one factor, and then use Method 1 from above.
Reminder: The Factor Theorem is defined as:
“If f(x) is a polynomial, and f(k)=0, then (x-k) is a factor of f(x)”
or
“If f \left(\dfrac{b}{a} \right)=0, then (ax-b) is a factor of f(x)”
When using the factor theorem here, you will need to try small values of k, e.g. f(1), f(-1), f(2), etc., until you find f(k)=0.
Cubic Graphs
You can sketch a cubic if you know its factors. You have to find where the function is 0.
All cubic graphs have a general shape:
- If the coefficient of x^3 is positive, then the graph goes from ‘the bottom left to the top right’
- If the coefficient of x^3 is negative, then the graph goes from ‘the top left to the bottom right’
The y-intercept of a cubic graph y=ax^{3}+bx^{2}+cx+d is always d, so by expanding brackets we can find where the graph crosses the y-axis.
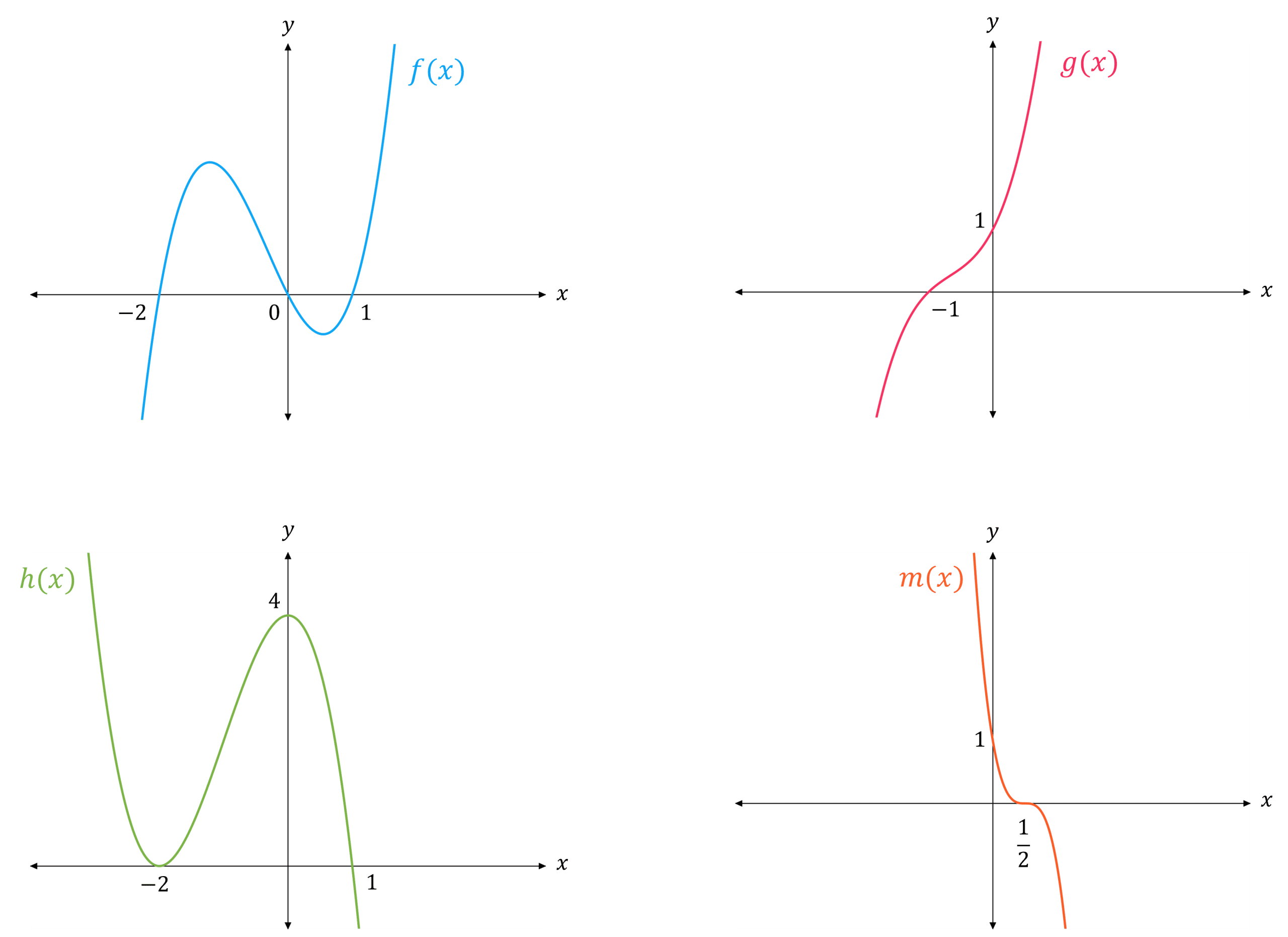
Example: Sketch the graphs of:
\begin{aligned} f(x) &= x(x-1)(x+2) \\ g(x) &= (x+1)(x^2 + x + 1) \\ h(x) &= (1-x)(x+2)^2 \\ m(x) &= (1-2x)^3 \end{aligned}
Example: Factorising Cubics using the Factor Theorem
Factorise f(x) = 3x^3 - 5x^2 - 4x + 4
[4 marks]
Try small values of k, e.g. f(1), f(-1), f(2), etc., until we find f(k)=0:
\begin{aligned} f(1) &= 3(1)^3 - 5(1)^2 - 4(1) + 4 = -2 \\ f(-1) &= 3(-1)^3 - 5(-1)^2 - 4(-1) + 4 = 0 \end{aligned}
f(-1) = 0, hence \textcolor{orange}{(x+1)} is a factor of f(x), by the Factor Theorem.
Write down the factor we know, \textcolor{orange}{(x+1)}, next to another set of brackets:
\textcolor{orange}{(x+1)}( \quad \quad \quad \quad \quad \quad ) = 3x^3 - 5x^2 - 4x + 4
Then, using Method 1, factorise the cubic:
We need the x^{2} term in our brackets to multiply by x to get 3x^{3}, so it must be 3x^{2}.
\textcolor{orange}{(x+1)}( 3x^{2} \quad \quad \quad \quad \quad ) = 3x^3 - 5x^2 - 4x + 4
1\times3x^{2}=3x^{2} but we want -5x^{2}, so we need -8x to multiply the x in the orange bracket to give us the difference of -8x^{2}.
\textcolor{orange}{(x+1)}( 3x^{2}-8x \quad \quad \quad ) = 3x^3 - 5x^2 - 4x + 4
To get the 4 at the end we multiply the 1 in the first bracket by the number that will go at the end of the second bracket, so this must be 4.
\textcolor{orange}{(x+1)}( 3x^{2}-8x+4) = 3x^3 - 5x^2 - 4x + 4
Finally, factorise the second bracket.
\textcolor{orange}{(x+1)}( 3x-2)(x-2) = 3x^3 - 5x^2 - 4x + 4
Cubics Example Questions
Question 1: Given that (2x+1) is a factor of f(x) = 2x^3 + 5x^2 - 4x - 3, express f(x) as a product of three linear factors.
[3 marks]
Write down the factor we know, (2x+1), next to another set of brackets:
(2x+1)( \quad \quad \quad \quad \quad \quad ) = 2x^3 + 5x^2 - 4x - 3
Put an x^2 term at the start of the second set of brackets – this will need to multiply together with 2x from the first bracket to make 2x^3:
(2x+1)(x^2 \quad \quad \quad \quad ) = 2x^3 + 5x^2 - 4x - 3
Find the constant term for the end of the second bracket – this will need to be multiplied together with 1 to make -3:
(2x+1)(x^2 \quad \quad \quad -3) = 2x^3 + 5x^2 - 4x - 3
The 2x and -3 above multiply to make -6x, but we need -4x. So we need an extra +2x from somewhere – we need to multiply 1 by 2x to make +2x:
(2x+1)(x^2 + 2x - 3) = 2x^3 + 5x^2 - 4x - 3
Check that this works, by multiplying out the brackets and seeing if this matches f(x):
\begin{aligned} &\, (2x+1)(x^2 + 2x - 3) \\ &= 2x^3 + 4x^2 - 6x + x^2 + 2x - 3 \\ &= 2x^3 + 5x^2 - 4x - 3 \end{aligned}
So, this works so far.
Factorise the quadratic x^2 + 2x -3 into 2 linear factors:
x^2 + 2x - 3 = (x+3)(x-1)
Finally, put it all together:
2x^3 + 5x^2 - 4x - 3 = (2x+1)(x+3)(x-1)
Question 2: Factorise f(x) = 3x^3 - x^2 - 20x - 12 fully.
[3 marks]
Try small values of k until f(k) = 0:
\begin{aligned} f(1) &= 3(1)^3 - (1)^3 - 20(1) - 12 = -30 \\ f(-1) &= 3(-1)^3 - (-1)^3 - 20(-1) - 12 = 4 \\ f(2) &= 3(2)^3 - (2)^2 - 20(2) - 12 = -32 \\ f(-2) &= 3(-2)^3 - (-2)^2 - 20(-2) - 12 = 0 \end{aligned}
f(-2) = 0, so (x+2) is a factor, by the Factor Theorem.
Then, write down this set of brackets next to a set of empty brackets, and factorise using the usual method:
\begin{aligned} (x+2)( \quad \quad \quad \quad \quad \quad ) &= 3x^3 - x^2 - 20x - 12 \\ 3x^3 - x^2 - 20x - 12 &= (x+2)(3x^2 - 7x - 6) \\ &= (x+2)(3x+2)(x-3) \end{aligned}
Question 3: f(x) = 3x^3 - 10x^2 + 9x - 2
a) Show that (3x-1) is a factor of f(x)
b) Hence, or otherwise, factorise f(x) fully.
c) Sketch y = f(x), making sure to clearly label any points at which the curve meets the x and y axes.
[7 marks]
a) (3x-1) is a factor of f(x) if f \left( \dfrac{1}{3} \right) = 0, by the Factor Theorem:
f \left( \dfrac{1}{3} \right) = 3 \left( \dfrac{1}{3} \right)^3 - 10 \left(\dfrac{1}{3} \right)^2 + 9 \left( \dfrac{1}{3} \right) - 2 = 0
Hence, (3x-1) is a factor of f(x)
b)
\begin{aligned} 3x^3 - 10x^2 + 9x - 2 &= (3x-1)(x^2 - 3x + 2) \\ &= (3x-1)(x-1)(x-2) \end{aligned}
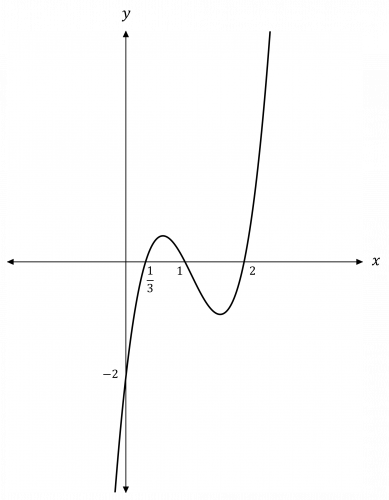
c) When f(x) = (3x-1)(x-1)(x-2) = 0, x = \dfrac{1}{3}, x = 1 or x = 2
Hence, the graph will cross the x-axis at x = \dfrac{1}{3}, x = 1 and x = 2
f(0) = 3(0)^3 - 10(0)^2 + 9(0) - 2 = -2
Hence, the graph will cross the y-axis at y = -2
So, we have enough information to sketch the graph:
Cubics Worksheet and Example Questions
Coordinate Geometry Curve
A LevelCurve Sketching
A LevelYou May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.







