Definite Integrals
Definite Integrals Revision
Definite Integrals
A definite integral is an integral with limits. The limits are represented as small numbers at the top and bottom of the integral. We integrate in exactly the same way, except we can leave out the constant of integration +c. Then, we get our final answer by substituting the limits into our integrated form, and taking the value for the lower limit away from the value for the upper limit.
Definite integrals are useful because they represent the area under the graph.
Make sure you are happy with the following topics before continuing.
Definite Integrals Have Limits
The limits of a definite integral are the small numbers at the top and bottom of the integral symbol. Once we have integrated, we substitute the limits in, then subtract the lower limit result from the upper limit result.
Example: Find \int ^{2}_{1}x^{2}dx
\begin{aligned}\int^{2}_{1}x^{2}dx&=\left[\dfrac{1}{3}x^{3}\right]^{2}_{1}\\[1.2em]&=\left( \dfrac{1}{3}\times2^{3}\right) -\left( \dfrac{1}{3}\times1^{3}\right) \\[1.2em]&=\dfrac{8}{3}-\dfrac{1}{3}\\[1.2em]&=\dfrac{7}{3}\end{aligned}
Definite Integrals are the Area Under the Graph
Definite integrals represent the area under the graph. For example, to find the area under the graph between -2 and 2 of y=x^{2}-4, we would do \int^{2}_{-2}x^{2}-4dx.
Note: Using this metric, area below the x axis is counted as negative.
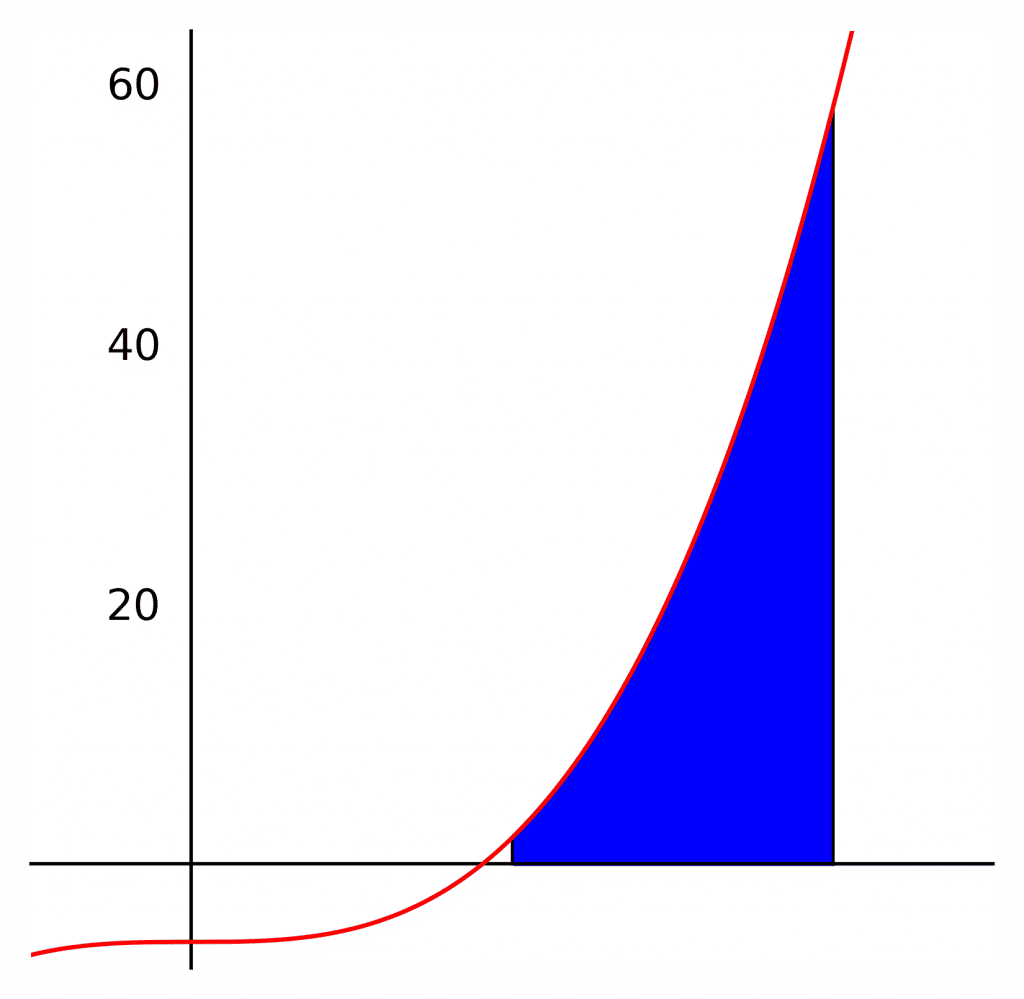
Example: Find the area under the graph y=x^{3}-6 between x=2 and x=4.
\begin{aligned}\text{area}&=\int^{4}_{2}x^{3}-6dx\\[1.2em]&=\left[\dfrac{1}{4}x^{4}-6x\right]^{4}_{2}\\[1.2em]&=\left( \dfrac{1}{4}\times4^{4}\right) -\left( 6\times4\right) -\left( \dfrac{1}{4}\times2^{4}\right) +\left( 6\times2\right) \\[1.2em]&=\left( \dfrac{1}{4}\times256\right) -24-\left( \dfrac{1}{4}\times16\right) +12\\[1.2em]&=64-24-4+12\\[1.2em]&=48\end{aligned}
A Level Maths Predicted Papers 2024
The MME A level maths predicted papers are an excellent way to practise, using authentic exam style questions that are unique to our papers. Our examiners have studied A level maths past papers to develop predicted A level maths exam questions in an authentic exam format. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
A Level Maths Revision Cards
The best A level maths revision cards for AQA, Edexcel, OCR, MEI and WJEC. MME is here to help you prepare effectively for your A Level maths exams. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
Adding Integrals
Sometimes, the area you have to figure out will not always be bounded by one function to integrate. In this case, you often have to add two integrals together.
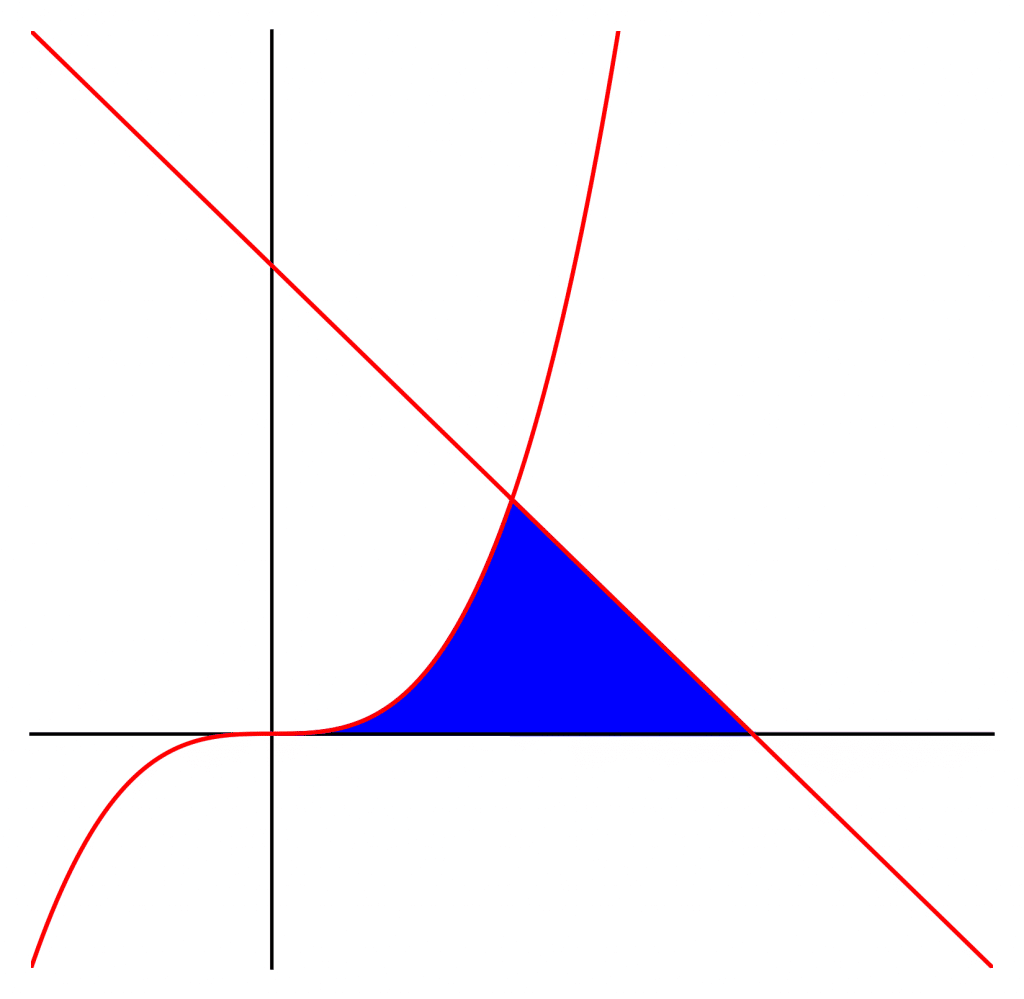
Example: Find the area between the x axis, the graph y=x^{3} and y=2-x.
The area runs from x=0 to x=2.
The graphs intersect at x=1, so the area changes from being under y=x^{3} to being under y=2-x at x=1.
Hence, we can find the area:
Subtracting Integrals
Some problems involving areas on graphs require you to subtract integrals. Generally, these questions take the form of asking you to find the area between two curves. We solve them by finding the entire area under the upper curve, then subtracting the area under the lower curve.
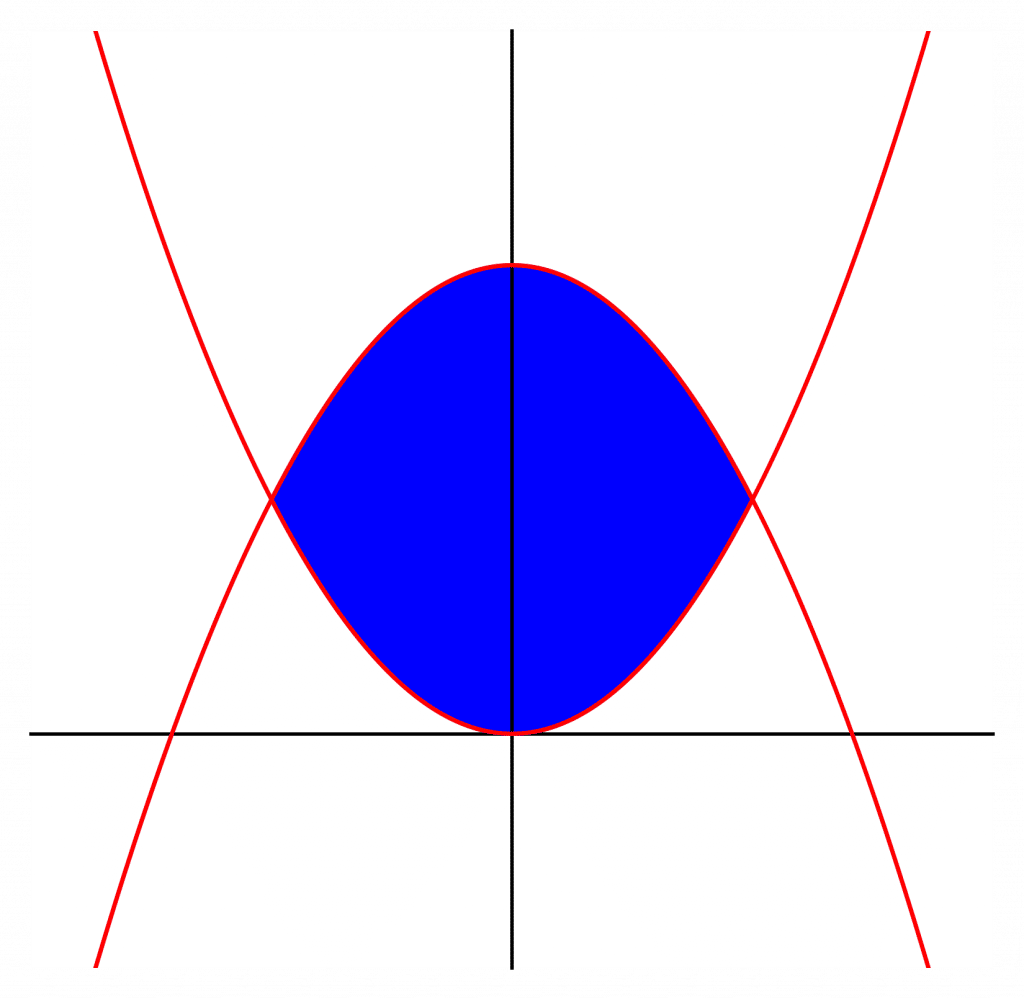
Example: Find the area between the curves y=x^{2} and y=2-x^{2}.
The area runs from x=-1 to x=1.
The upper curve is y=2-x^{2}. Integrating this gives the entire area under this curve.
The lower curve is y=x^{2}. Subtracting the integral of this gets rid of the area we don’t want.
Definite Integrals Example Questions
Question 1: Find:
i) \int^{3}_{1}x^{3}dx
ii) \int^{4}_{0}2x+1dx
iii) \int^{1}_{-1}x^{-3}dx
[3 marks]
i)\begin{aligned}\int^{3}_{1}x^{3}dx&=\left[\dfrac{1}{4}x^{4}\right]^{3}_{1}\\[1.2em]&=\left( \dfrac{1}{4}\times3^{4}\right) -\left( \dfrac{1}{4}\times1^{4}\right) \\[1.2em]&=\left( \dfrac{1}{4}\times81\right) -\left( \dfrac{1}{4}\times1\right) \\[1.2em]&=\dfrac{81}{4}-\dfrac{1}{4}\\[1.2em]&=\dfrac{80}{4}\\[1.2em]&=20\end{aligned}
ii)\begin{aligned}\int^{4}_{0}2x+1dx&=[x^{2}+x]^{4}_{0}\\[1.2em]&=4^{2}+4-0^{2}+0\\[1.2em]&=16+4\\[1.2em]&=20\end{aligned}
iii)\begin{aligned}\int^{1}_{-1}x^{-3}dx&=\left[-\dfrac{1}{2}x^{-2}\right]^{1}_{-1}\\[1.2em]&=\left( -\dfrac{1}{2}\times1^{-2}\right) +\left( \dfrac{1}{2}\times(-1)^{-2}\right) \\[1.2em]&=-\dfrac{1}{2}+\dfrac{1}{2}\\[1.2em]&=0\end{aligned}
Question 2: Find:
i) \int^{3}_{-3}x^{2}+4x+8dx
ii) \int^{5}_{1}x^{\frac{6}{7}}-\sqrt{x}dx
iii) \int^{200}_{1}15x^{\frac{1}{3}}+10x^{\frac{1}{4}}-3x^{\frac{5}{12}}dx
[6 marks]
i)
\begin{aligned}&\int^{3}_{-3}\left( x^{2}+4x+8\right) dx=\left[\dfrac{1}{3}x^{3}+2x^{2}+8x\right]^{3}_{-3}\\[1.2em]&=\left( \dfrac{1}{3}\times3^{3}\right) +\left( 2\times3^{2}\right) +\left( 8\times3\right) -\left( \dfrac{1}{3}\times(-3)^{3}\right) -\left( 2\times(-3)^{2}\right) -\left( 8\times(-3)\right) \\[1.2em]&=\left( \dfrac{1}{3}\times27\right) +\left( 2\times9\right) +24+\left( \dfrac{1}{3}\times27\right) -\left( 2\times9\right) +24\\[1.2em]&=9+18+24+9-18+24\\[1.2em]&=66\end{aligned}
ii)
\begin{aligned}&\int^{5}_{1}\left( x^{\frac{6}{7}}-\sqrt{x}\right) dx=\int^{5}_{1}\left( x^{\frac{6}{7}}-x^{\frac{1}{2}}\right) dx\\[1.2em]&=\left[\dfrac{7}{13}x^{\frac{13}{7}}-\dfrac{2}{3}x^{\frac{3}{2}}\right]^{5}_{1}\\[1.2em]&=\left( \dfrac{7}{13}\times5^{\frac{13}{7}}\right) -\left( \dfrac{2}{3}\times5^{\frac{3}{2}}\right) -\left( \dfrac{7}{13}\times1^{\frac{13}{7}}\right) +\left( \dfrac{2}{3}\times1^{\frac{3}{2}}\right) \\[1.2em]&=\left( \dfrac{7}{13}\times5^{\frac{13}{7}}\right) -\left( \dfrac{2}{3}\times5^{\frac{3}{2}}\right) -\dfrac{7}{13}+\dfrac{2}{3}\\[1.2em]&=3.37\end{aligned}
iii)
\begin{aligned}&\int^{200}_{1}\left( 15x^{\frac{1}{3}}+10x^{\frac{1}{4}}-3x^{\frac{5}{12}}\right) dx\\[1.2em]&=\left[\left( 15\times\dfrac{3}{4}x^{\frac{4}{3}}\right) +\left( 10\times\dfrac{4}{5}x^{\frac{5}{4}}\right) -\left( 3\times\dfrac{12}{17}x^{\frac{17}{12}}\right) \right]^{200}_{1}\\[1.2em]&=\left[\dfrac{45}{4}x^{\frac{4}{3}}+8x^{\frac{5}{4}}-\dfrac{36}{17}x^{\frac{17}{12}}\right]^{200}_{1}\\[1.2em]&=\left( \dfrac{45}{4}\times200^{\frac{4}{3}}\right) +\left( 8\times200^{\frac{5}{4}}\right) -\left( \dfrac{36}{17}\times200^{\frac{17}{12}}\right) \\[1.2em]&\left( -\dfrac{45}{4}\times1^{\frac{4}{3}}\right) -\left( 8\times1^{\frac{5}{4}}\right) +\left( \dfrac{36}{17}\times1^{\frac{17}{12}}\right) \\[1.2em]&=\left( \dfrac{45}{4}\times200^{\frac{4}{3}}\right) +\left( 8\times200^{\frac{5}{4}}\right) -\left( \dfrac{36}{17}\times200^{\frac{17}{12}}\right) \\[1.2em]&-\dfrac{45}{4}-8+\dfrac{36}{17}\\[1.2em]&=15300\end{aligned}Question 3: Find the area bounded by the x axis, the graph y=\sqrt{x} and the graph y=10-x^{\frac{3}{2}}
[6 marks]
Graphs intersect at (4,2), so we want the area under y=\sqrt{x} from 0 to 4 added to the area under y=10-x^{\frac{3}{2}} from 4 to where this graph touches the x axis.
Find where y=10-x^{\frac{3}{2}} touches the x axis.
0=10-x^{\frac{3}{2}}
x^{\frac{3}{2}}=10
x=10^{\frac{2}{3}}
Putting this all together:
\begin{aligned}\text{area}&=\int^{4}_{0}\sqrt{x}dx+\int^{10^{\frac{2}{3}}}_{4}\left( 10-x^{\frac{3}{2}}\right) dx\\[1.2em]&=\int^{4}_{0}x^{\frac{1}{2}}dx+\left[10x-\dfrac{2}{5}x^{\frac{5}{2}}\right]^{10^{\frac{2}{3}}}_{4}\\[1.2em]&=\left[\dfrac{2}{3}x^{\frac{3}{2}}\right]^{4}_{0}+\left( 10\times10^{\frac{2}{3}}\right) -\left( \dfrac{2}{5}\times(10^{\frac{2}{3}})^{\frac{5}{2}}\right)-\left( 10\times4\right) +\left( \dfrac{2}{5}\times4^{\frac{5}{2}}\right) \\[1.2em]&=\left( \dfrac{2}{3}\times4^{\frac{3}{2}}\right) -\left( \dfrac{2}{3}\times0^{\frac{3}{2}}\right) +10^{\frac{5}{3}}-\left( \dfrac{2}{5}\times10^{\frac{5}{3}}\right) -40+\left( \dfrac{2}{5}\times32\right) \\[1.2em]&=\left( \dfrac{2}{3}\times8\right) +\left( \dfrac{3}{5}\times10^{\frac{5}{3}}\right) -40+\dfrac{64}{5}\\[1.2em]&=5.98\end{aligned}Question 4: Find the area bounded by the y axis, the graph y=x^{5} and the graph y=x^{2}-4x+36
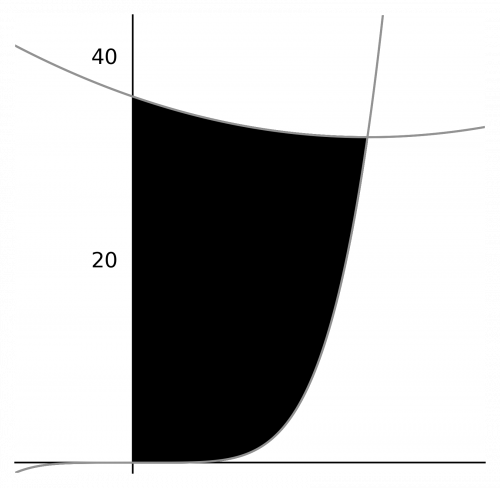
[4 marks]
From the graph we can see that we want the area under y=x^{2}-4x+36 minus the area under y=x^{5}, and the graphs intersect at (2,32) so our area runs from 0 to 2.
\begin{aligned}\text{area}&=\int^{2}_{0}\left( x^{2}-4x+36\right) dx-\int^{2}_{0}x^{5}dx\\[1.2em]&=\left[\left( \dfrac{1}{3}x^{3}\right) -2x^{2}+36x\right]^{2}_{0}-\left[\dfrac{1}{6}x^{6}\right]^{2}_{0}\\[1.2em]&=\left( \dfrac{1}{3}\times2^{3}\right) -\left( 2\times2^{2}\right) +\left( 36\times2\right) -\left( \dfrac{1}{3}\times0^{3}\right) +\left( 2\times0^{2}\right) -\left( 36\times0\right) -\left( \dfrac{1}{6}\times2^{6}\right) +\left( \dfrac{1}{6}\times0^{6}\right) \\[1.2em]&=\left( \dfrac{1}{3}\times8\right) -\left( 2\times4\right) +72-\left( \dfrac{1}{6}\times64\right) \\[1.2em]&=\dfrac{8}{3}-8+72-\dfrac{32}{3}\\[1.2em]&=64-\dfrac{24}{3}\\[1.2em]&=64-8\\[1.2em]&=56\end{aligned}Definite Integrals Worksheet and Example Questions
Calculus
A LevelYou May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.
