Graph Transformations
Graph Transformations Revision
Graph Transformations
You should have seen some graph transformations before, such as translations and reflections – recall that reflections in the x-axis flip f(x) vertically and reflections in the y-axis flip f(x) horizontally. Here, we will also look at stretches.
There are 4 main types of graph transformation that we will cover. Each transformation has the same effect on all functions.
Make sure you are happy with the following topics before continuing.
Type 1: y = f(x+k)
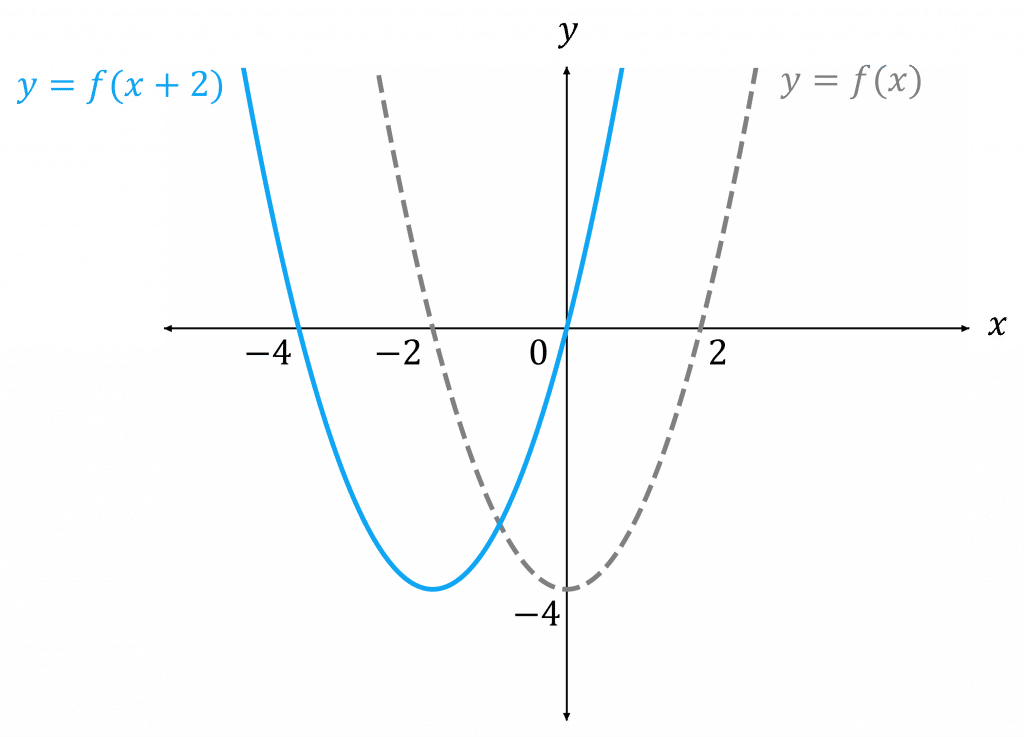

For the transformation y=f(x+k), for k>0:
- f(x+k) is f(x) moved k to the left
- f(x-k) is f(x) moved k to the right
In this example, we have f(x) = x^2 - 4 and y=f(x+2)
So, subtract 2 from the x-coordinates of f(x) to get y=f(x+2)
Type 2: y = f(x)+k
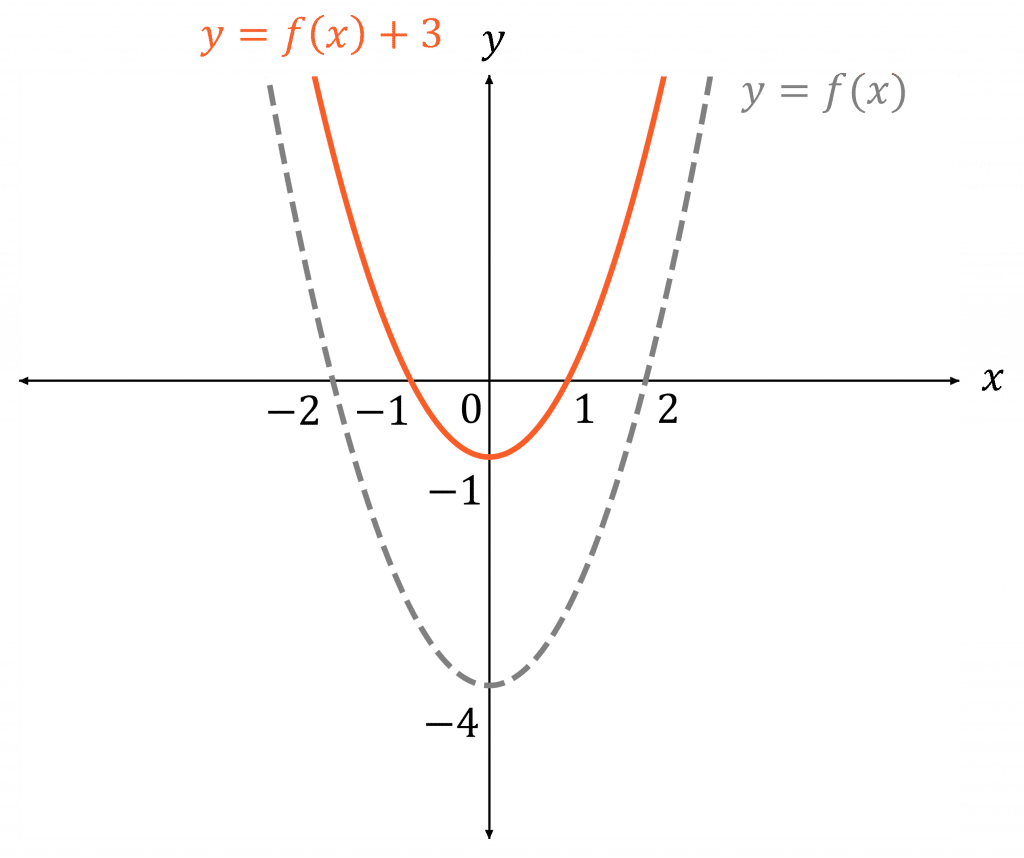

For the transformation y=f(x)+k, for k>0:
- f(x)+k is f(x) moved k upwards
- f(x)-k is f(x) moved k downwards
In this example, we have f(x) = x^2 - 4 and y=f(x)+3
So, add 3 to the y-coordinates of f(x) to get y=f(x)+3
Type 3: y = af(x)
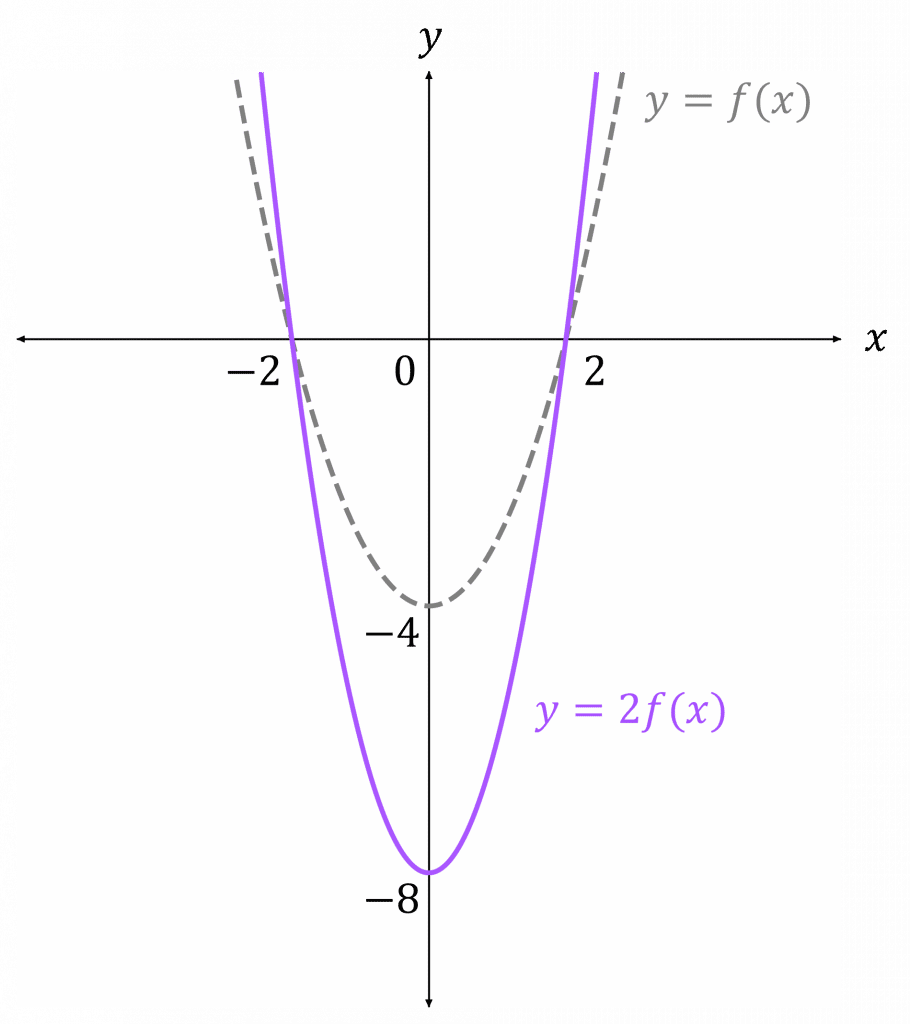

For the transformation y=af(x):
- If |a|>1 then af(x) is f(x) stretched vertically by a factor of a
- If 0<|a|<1 then f(x) is squashed vertically
- If a<0 then is f(x) also reflected in the x-axis
In this example, we have f(x) = x^2 - 4 and y=2f(x)
This is a stretch vertically, so multiply the y-coordinates of f(x) by 2 to get y=2f(x)
Type 4: y = f(ax)
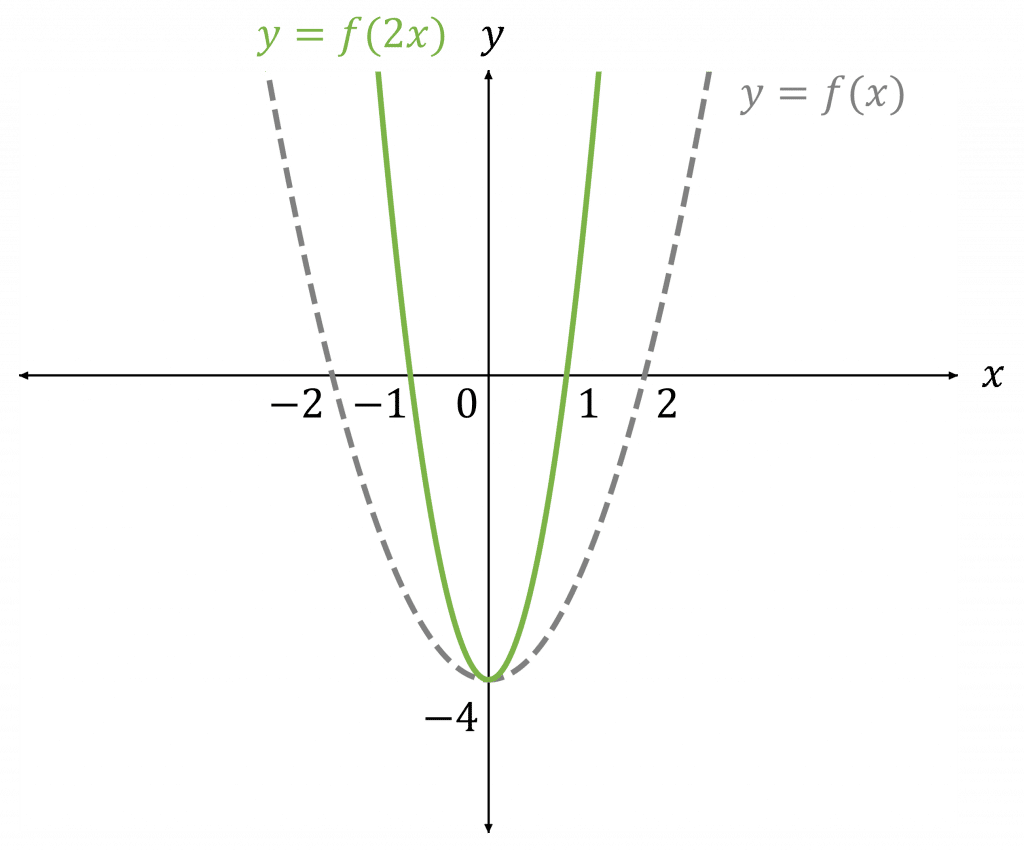

For the transformation y=f(ax):
- If |a|>1 then f(ax) is f(x) squashed horizontally by a factor of a
- If 0<|a|<1 then f(x) is stretched horizontally
- If a<0 then is f(x) also reflected in the y-axis
In this example, we have f(x) = x^2 - 4 and y=f(2x)
This is a squash horizontally, so divide the x-coordinates of f(x) by 2 (or multiply by \dfrac{1}{2}) to get y=f(2x)
Note:
- For these transformations, any asymptotes need to be moved correspondingly.
- A squash by a factor of a is equivalent to a stretch by a factor of \dfrac{1}{a}
- When drawing graph transformation, only a sketch including important points is necessary.
Combinations of Transformations
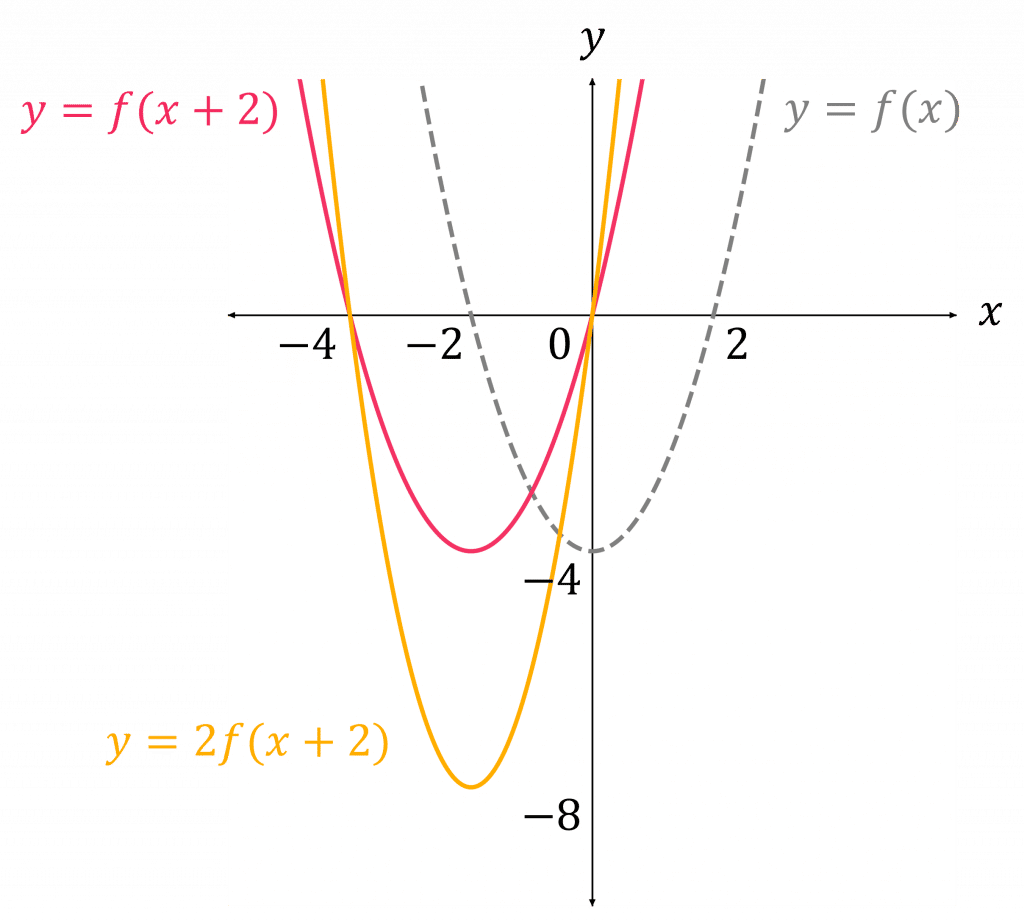

For combinations of transformations, it is easy to break them up and do them one step at a time (do the bit in the brackets first). You can sketch the graph at each step to help you visualise the whole transformation.
e.g. for f(x) = x^2 - 4 and y=2f(x+2), draw the graph of
y=f(x+2) first, and then use this graph to draw the graph of
y=2f(x+2)
Note: These transformations can also be combined with modulus functions.
Graph Transformations Example Questions
Question 1: The function f(x) is shown on the graph below.
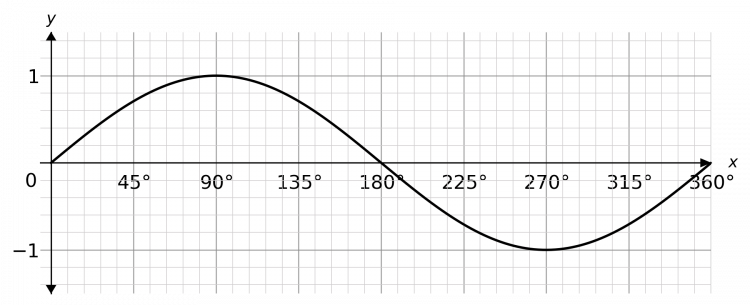
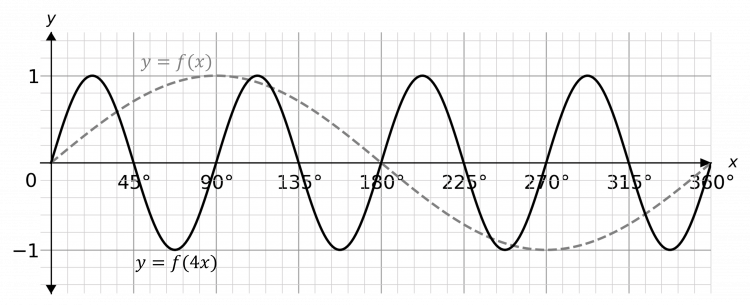
Sketch the graph of y = f(4x)
[2 marks]
y = f(4x) means that the graph of f(x) is squashed horizontally by a factor of 4.
Hence, the graph will look like:
Question 2: The function f(x) is shown on the graph below.
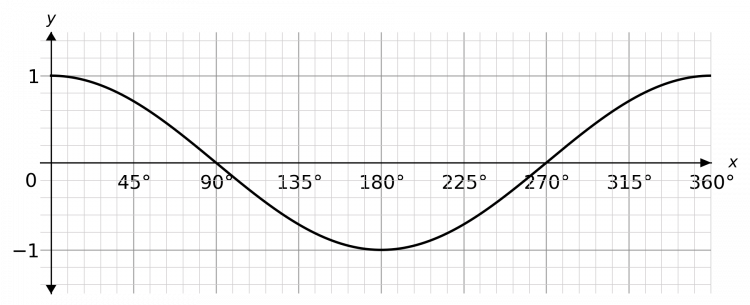
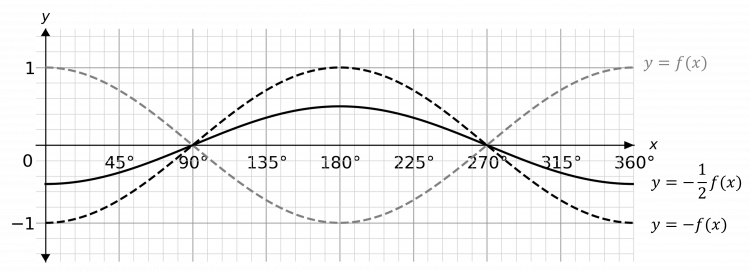
Sketch the graph of y = - \dfrac{1}{2} f(x)
[3 marks]
Firstly, since the coefficient before f(x) is negative, we need to reflect f(x) in the x-axis.
The coefficient of \dfrac{1}{2} before -f(x) means that the graph of -f(x) is squashed vertically by a factor of 2.
Hence, the graph will look like:
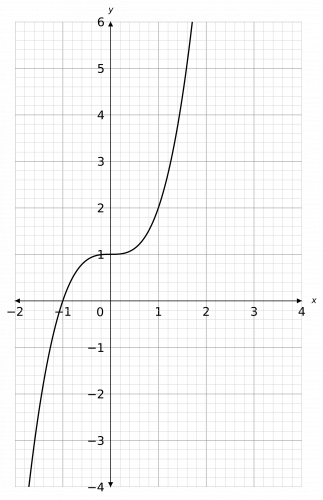
Question 3: The function f(x) is shown on the graph below.
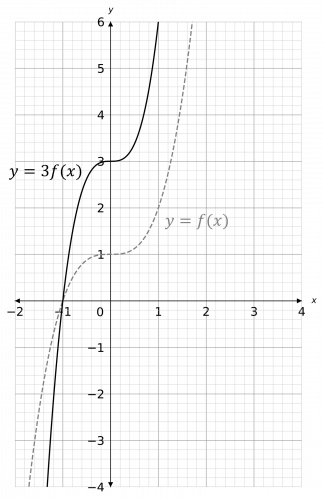
Sketch the graph of y = 3f(x) - 1
[3 marks]
Split the transformation up into 2 parts – firstly sketch y=3f(x) which is a stretch vertically by a scale factor of 3 (multiply the y-coordinates by 3:
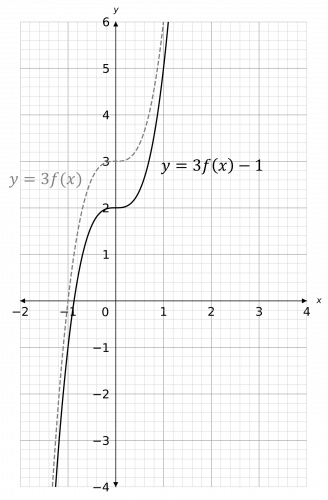
Then, do the second transformation – y=3f(x)-1 means that we need to move the graph down by 1 (subtract 1 from the y-coordinates):
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.







