Proportion
Proportion Revision
Proportion
Two variables are proportional if as one variable changes, the other variable changes in a specific way. Variables can either be directly proportional or inversely proportional.
Direct Proportion
If two variables are directly proportional, then as one increases, the other increases by the same scale factor (at the same rate). For two variables, say x and y, we can write
y \propto x
which means “y is directly proportional to x” (the \propto symbol means proportional).
This expression is equivalent to writing
y = \textcolor{orange}{k}x
where \textcolor{orange}{k} is the constant of proportionality – this tells us how x and y are related to each other.
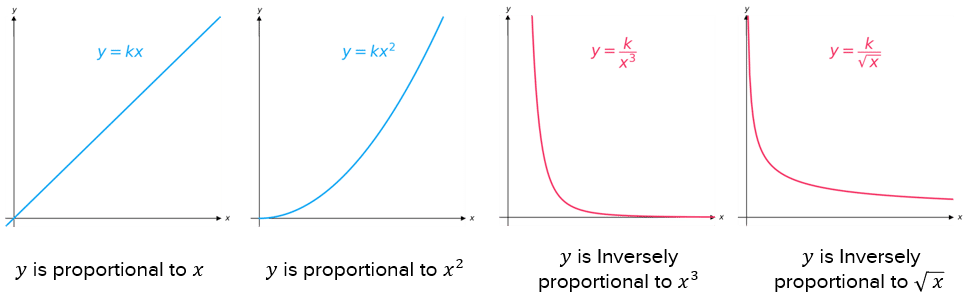
There are other types of direct proportion, such as y \propto x^2 or y \propto \sqrt{x}, which can be seen in the table below.

Inverse Proportion
If two variables are inversely proportional, then as one increases, the other decreases by the same scale factor (at the same rate). For two variables, say x and y, we can write
y \propto \dfrac{1}{x}
which means “y is inversely proportional to x” or “y is directly proportional to \dfrac{1}{x}”.
This expression is equivalent to writing
y = \dfrac{\textcolor{orange}{k}}{x}
There are other types of inverse proportion, such as y \propto \dfrac{1}{x^2} or y \propto \dfrac{1}{\sqrt{x}}, which can be seen in the table below.

Proportionality Graphs
The equations of direct proportion and inverse proportion can be plotted as graphs:
Example 1: Direct Proportion
If y is directly proportional to x^2 and y=36 when x=3, find the value of y when x=5.
[3 marks]
Step 1: y \propto x^2, so we can write this as an equation involving the constant of proportionality: y = kx^2
Step 2: We are given that y = 36 and x = 3. Substitute these into the equation above and solve to find k:
\begin{aligned} 36 &= k \times 3^2 \\ 36 &= 9k \\ \textcolor{orange}{k} &\textcolor{orange}{= 4} \end{aligned}
Hence, the equation becomes: y = \textcolor{orange}{4}x^2
Step 3: Find the value of y when x=5 by substituting in x=5 into the equation:
y = \textcolor{orange}{4} \times 5^2 = 100
Example 2: Inverse Proportion
The density of a solid, \rho \text{ kg/m}^3, is modelled as being inversely proportional to the volume of the solid, V \text{ m}^3.
a) A solid with density 40 \text{ kg/m}^3 has a volume of 0.05 \text{ m}^3. Find the constant of proportionality.
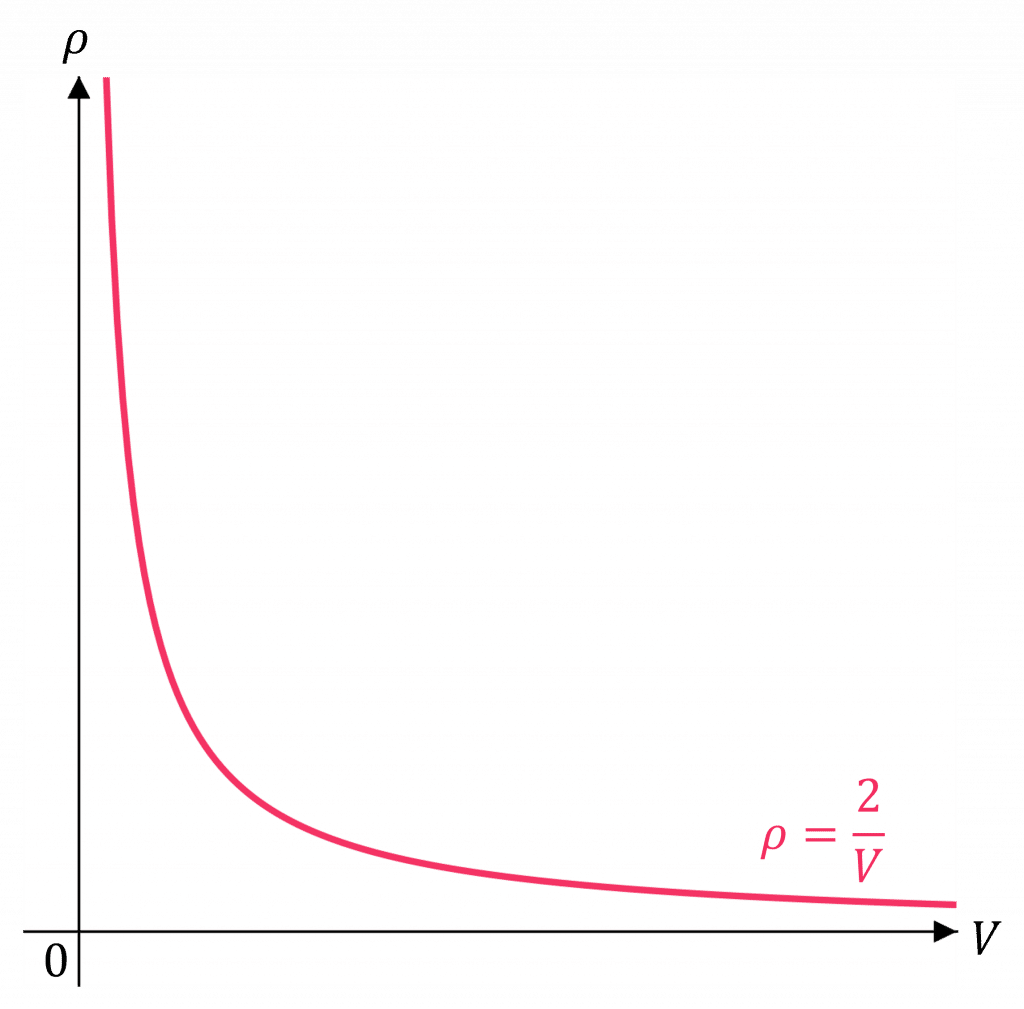
b) Sketch the graph of \rho against V.
[4 marks]

a) \rho \propto \dfrac{1}{V} is equivalent to \rho = \dfrac{k}{V}
When \rho = 40, V = 0.05, so
40 = \dfrac{k}{0.05} \Rightarrow \textcolor{orange}{k} = 40 \times 0.05 = \textcolor{orange}{2}
b) \rho = \dfrac{2}{V} is of the form \rho = kV^n where \textcolor{orange}{k = 2} and n = -1.
The volume cannot be negative, so we only need to sketch the top-right quadrant of the graph.
Note: There will be asymptotes here at \rho = 0 and V = 0.
Proportion Example Questions
Question 1: If y is inversely proportional to \sqrt{x} and y = 8 when x = 9, find the value of x when y = 6.
[3 marks]
y \propto \dfrac{1}{\sqrt{x}}, so we can write this as y = \dfrac{k}{\sqrt{x}}
We are given that y = 8, when x = 9, so substitute these into the equation and solve to find k:
\begin{aligned} 8 &= \dfrac{k}{\sqrt{9}} \\[1.2em] 8 &= \dfrac{k}{3} \\[1.2em] k &= 24 \end{aligned}
So, the equation is
y = \dfrac{24}{\sqrt{x}}
Then, find the value of x when y = 6, by substituting in y = 6 into the equation and solving for x:
\begin{aligned} 6 &= \dfrac{24}{\sqrt{x}} \\[1.2em] \sqrt{x} &= \dfrac{24}{6} \\[1.2em] \sqrt{x} &= 4 \\[1.2em] x &= 16 \end{aligned}
Question 2: The kinetic energy, E \text{ J} of an object is directly proportional to the velocity of the object, v \text{ m/s}, squared.
a) An object travelling at a velocity of 10 \text{ m/s} has a kinetic energy of 3000 \text{ J}. Find the constant of proportionality.
b) Find the kinetic energy of the object when it is travelling at a velocity of 4 \text{ m/s}.
[3 marks]
a) E \propto v^2, which can be written as E=kv^2
When v = 10, E = 3000, so
\begin{aligned} 3000 &= k \times 10^2 \\ 3000 &= 100k \\ k &= \dfrac{3000}{100} = 30 \end{aligned}
b) E = 30v^2
Substitute in v=4 into the equation to find the kinetic energy of the object if it is travelling at a velocity 4 \text{ m/s}:
E = 30 \times 4^2 = 30 \times 16 = 480 \text{ J}
Question 3: The work done by an object, W \text{ Nm}, is modelled as being directly proportional to the distance moved by the object, d \text{ m}.
a) The work done by an object that is moved by 12 \text{ m} is 60 \text{ Nm}. Find the constant of proportionality.
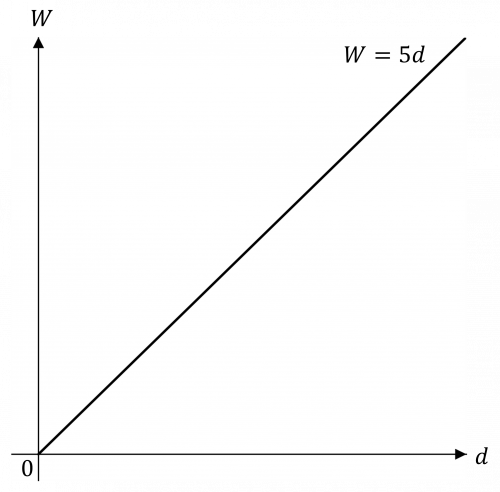
b) Sketch the graph of W against d.
c) Find the work done by the object if it is moved by a distance of 25 \text{ m}.
[5 marks]
a) W \propto d, which is equivalent to W = kd.
When d = 12, W = 60, therefore
60 = k \times 12 \Rightarrow k = 60 \div 12 = 5
b) W = 5d will be a straight line passing through the origin. You will only need to sketch the graph in the top right quadrant since distance cannot be negative.
(The gradient of the line is 5, but since we are only doing a sketch we do not need to write any values on the axes, so we can just draw any straight line passing through the origin with a positive gradient).
The graph will look like:
c) W = 5d
Substitute in d=25 into the equation to find the work done by the object if it is moved by 25 \text{ m}:
W = 5 \times 25 = 125 \text{ Nm}
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.







