Resolving Forces
Resolving Forces Revision
Resolving Forces
In the Forces section. we mentioned that forces have components. In most systems we work with, this will generally be resolved horizontally and vertically.
You’ll need to make sure your trigonometry is up to scratch!
Make sure you are happy with the following topics before continuing.
Simple Model
Example: Two people are pushing and pulling on a box such that they are both providing force in the same direction.
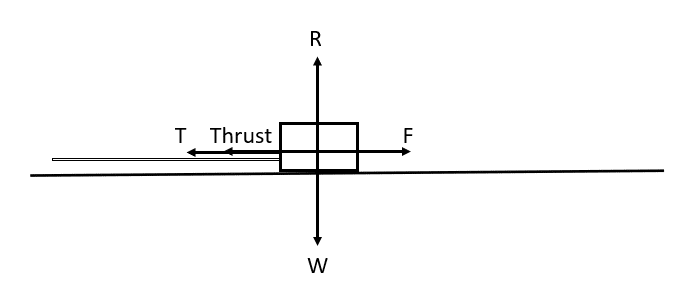
This example is already resolved into horizontal and vertical components, as the box is on a flat surface.
Let’s say the system is in equilibrium – there is no resultant force; the horizontal forces sum to 0\text{ N}, and the vertical forces sum to 0\text{ N}, also.
So, T + \text{Thrust} = F and R = W.
Say that the box weighs 5\text{ kg}. Then, from W = mg, we have W = 5 \times 9.8 = 49\text{ N}, meaning that the normal reaction force, R, = 49\text{ N}.
On a Tilted Plane
Example: A car is driving up a hill while being towed by a truck.
Again, let’s say the system is in equilibrium.
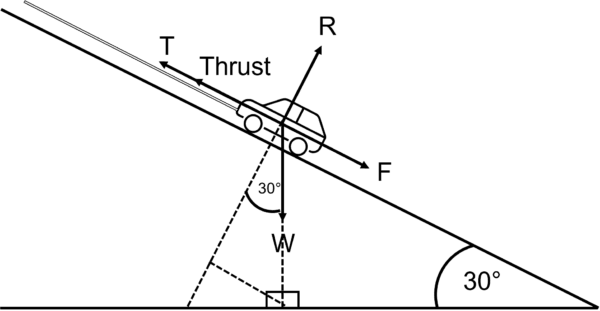
Now, we need to resolve horizontally and vertically, as we can see that W isn’t perpendicular to T, \text{Thrust} and F.
Let’s rotate the system again.
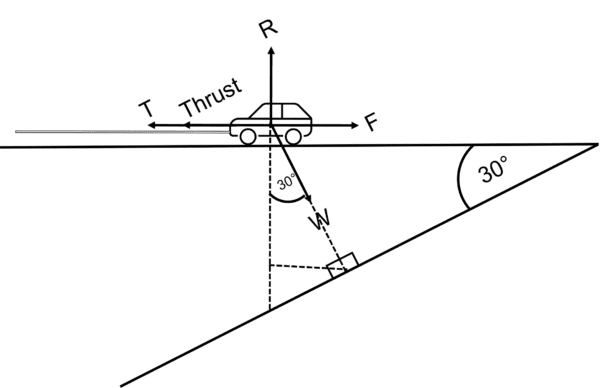
Resolving in the “new horizontal”, we have T + \text{ Thrust} = F + W\sin 30°.
Resolving in the “new vertical”, we have R = W\cos 30°.
Note:
Remember, for any x,
-1 \leq \sin x \leq 1
and
-1 \leq \cos x \leq 1.
If you are resolving in any direction and a component of the force is greater than the force itself, something has gone wrong.
Resolving in Vector Form
We can also resolve forces that are given in vector format. Generally, for a 2D system, we’ll have \textbf{i} indicating a horizontal component and \textbf{j} representing the vertical component, though this is not always the case.
The process here is pretty intuitive – operate in the same way you would in standard algebra.
For example, let F_1 = (2\textbf{i} + \textbf{j}), F_2 = (4\textbf{i}), F_3 = (3\textbf{j}).
Then, F_1 + F_2 - F_3 = (2 + 4)\textbf{i} + (1 - 3)\textbf{j} = 6\textbf{i} - 2\textbf{j}.
Resolving Forces Example Questions
Question 1: A 2\text{ kg} ball is rolled along a flat surface with a fixed horizontal force of 15\text{ N}. The ball is rolled into the mud, and stops moving. What is the frictional force acting on the ball once it has stopped moving? What is the reaction force applied?
[2 marks]
Take g = 9.8\text{ ms}^{-2}.
The ball stops moving – this means that the system is in equilibrium.
The friction force is equal to the thrust force, 15\text{ N}.
The reaction force is equal to the weight in this scenario. That is, R = W. Since W = mg, we have R = W = 2 \times 9.8 = 19.6\text{ N}.
Question 2: A car’s handbrake is applied on a 15° decline.
Given that the car has a mass of 1000\text{ kg} and assuming that friction has no effect on the system, what is the resistive force, F, applied to the car by the handbrake?
Assume g = 9.8\text{ ms}^{-2}.
[2 marks]
As we know the car is static, we know F will be equal to the forces acting in the opposite direction.
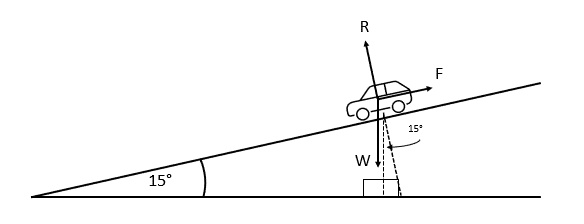
Resolving parallel to F, we have
\begin{aligned}F&=W\sin 15°\\[1.2em]&=mg\sin 15°\\[1.2em]&=1000 \times 9.8 \times \sin 15°\\[1.2em]&=2536.43 \text{ N (to 2dp)}\end{aligned}
Question 3: We have a particle being pulled from 4 different directions. It experiences forces
(\textbf{i} + 2\textbf{j}), \left( \dfrac{5}{2}\textbf{i} - \dfrac{1}{2}\textbf{j}\right) , (-2\textbf{i}, -\textbf{j}) and (-\textbf{i}).
Give the vector for the resultant force applied.
[1 mark]
We have (\textbf{i} + 2\textbf{j}), \left( \dfrac{5}{2}\textbf{i} - \dfrac{1}{2}\textbf{j}\right) , (-2\textbf{i}, -\textbf{j}) and (-\textbf{i}).
Then, \left( \left( 1 + \dfrac{5}{2} - 2 - 1\right) \textbf{i} + \left( 2 - \dfrac{1}{2} - 1\right) \textbf{j}\right) = \left( \dfrac{1}{2}\textbf{i} + \dfrac{1}{2}\textbf{j}\right)
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.







