Rigid Bodies and Friction
Rigid Bodies and Friction Revision
Reactions Can Have Components
- If a rod is connected to a plane by a hinge or pivot, and there are forces that are not parallel to the rod acting on the rod, then the reaction force on the rod at the wall will not be perpendicular to the wall. We deal with this by resolving it into parallel and perpendicular components (i.e. components in the direction of the rod and in the direction of the wall).
- If the rod is not attached to the wall, but is instead held against the wall by friction, the friction replaces the vertical component of the reaction force, and we only get the component perpendicular to the wall, like usual.
- Sometimes, a rod will be positioned against two surfaces (such as a ladder that is on both a floor and a wall – a very common exam question). There could be friction on none, one, or two of the surfaces. The question should indicate which surfaces are rough and which surfaces are smooth.
- Questions can also be asked about bodies leaning against surfaces that are neither horizontal nor vertical. As ever, just place the reaction force perpendicular to the surface and the friction force parallel to the surface, and you are good to go.
- If a rod has a support that it is resting on along its length, then the reaction force is perpendicular to the rod.
- Finally, some questions ask you to find a range for the coefficient of friction, \mu. To do this, treat the system as if it were in limiting equilibrium, but when you come to work out the coefficient of friction, replace F=\mu R with F\leq\mu R.
Example 1: Rod Held by a Pivot
A horizontal rod is held against a vertical wall by a pivot. The weight of the rod is 22\text{ N}, and it is held by a bar at 60\degree, providing a tension of 50\text{ N}. Find the horizontal and vertical components of the reaction force of the rod against the wall.
[4 marks]
First, draw a diagram.
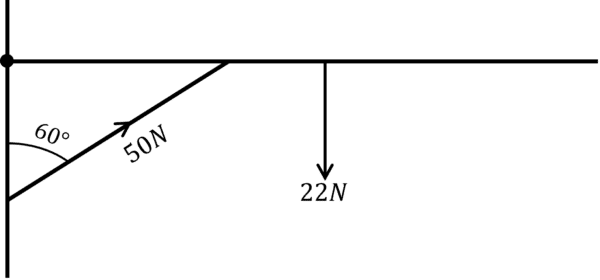
Resolve vertically:
50\cos(60)=R_{v}+22
25=R_{v}+22
R_{v}=3 \text{ N}
Resolve horizontally:
50\sin(60)=R_{h}
R_{h}=25\sqrt{3}
R_{h}=43.3 \text{ N}
Example 2: Ladder
A ladder is stood upon a rough horizontal floor and leaning against a smooth vertical wall. Given that it has a mass of 12\text{ kg}, and the reaction force from the vertical wall is 29.4\text{ N}, find the coefficient of friction of the floor.
[3 marks]
First draw a diagram.
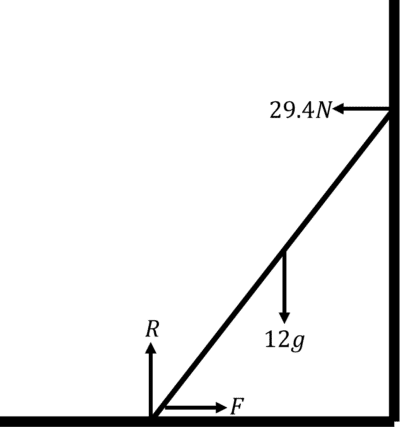
Resolve vertically:
R=12gResolve horizontally:
F=29.4\text{ N}
F \leq \mu R
29.4 \leq 12g\mu
29.4 \leq 117.6\mu
\mu\geq \dfrac{29.4}{117.6}
\mu \geq 0.25
Rigid Bodies and Friction Example Questions
Question 1: A 30\text{ cm} shelf is propped up by a support beam, as below. Given that the support beam can supply a maximum of 300\text{ N}, could the shelf support two \text{7.5 kg} trophies at distances 15\text{ cm} and 25\text{ cm}?
Also, calculate the horizontal and vertical reaction forces at the point where the shelf meets the wall.
Assume that the shelf is weightless.
[6 marks]
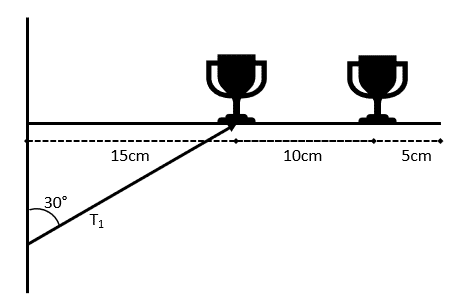
Take the moment about the point where the shelf meets the wall.
Clockwise: (0.15 \times 7.5 \times 9.8) + (0.25 \times 7.5 \times 9.8) = 0.4 \times 7.5 \times 9.8 = 29.4\text{ Nm}
Anticlockwise: The maximum perpendicular force is 0.15 \times 300\cos 30° = 38.97\text{ Nm (to } 2\text{ dp)}
The force from the support beam exceeds the force from the trophies, so the shelf will stay up.
For the entire system, vertically:
R_{Vwall} + T_{1}\cos 30° = 2 \times 7.5 \times 9.8 = 147
Since we know that
T_{1} = \dfrac{29.4}{0.15\cos 30°} = 226.3, we have R_{Vwall} = -49\text{ N}
so this reactionary force acts downwards at the wall.
For the entire system, horizontally:
R_{Hwall} = T_1 \sin 30° = 113.16\text{ N}
Question 2: An art piece can be modelled as a uniform rod weighing 5\text{ kg}, held up by two large, weightless pipes.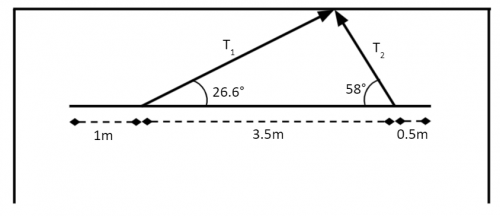
Given that the piece is in equilibrium, find T_1 and T_2, using the moments technique.
[4 marks]
Resolving horizontally, we have
T_1\cos 26.6 = T_2\cos 58
Rearrange this to get
T_1 = T_2\dfrac{\cos 58}{\cos 26.6}
Using moments about the left end of the rod:
Clockwise: 2.5 \times 5 \times 9.8 = 122.5\text{ Nm}
Anticlockwise: T_1\sin 26.6 + 4.5T_2\sin 58
122.5 = T_1\sin 26.6 + 4.5T_2\sin 58\\
122.5 = (T_2 \times \tan 26.6 \times \cos 58) + (4.5T_2\sin 58)\\
T_2 = \dfrac{122.5}{(\tan 26.6 \times \cos 58) + 4.5\sin 58} = 30.01\text{ N}\\
T_1 = 17.79\text{ N}
Question 3: Consider a ladder placed on a rough floor, at an angle of 60\degree to the horizontal. The ladder rests on a vertical wall, and the coefficient of friction of both the floor and the wall is 0.5. The ladder has a mass of 20\text{ kg}, which is evenly distributed across its 1\text{ m} length. By taking moments about the base, or otherwise, find the reaction forces from both the floor and the wall.
[5 marks]
Draw a diagram.

Evenly distributed so the weight acts in the middle, 0.5\text{ m} from the base.
Take moments about the base:
R_{2}\sin(60)=0.5R_{2}\cos(60)+0.5\times20g\cos(60)
\dfrac{\sqrt{3}}{2}R_{2}=\dfrac{1}{4}R_{2}+5g
\left(\dfrac{\sqrt{3}}{2}-\dfrac{1}{4}\right)R_{2}=5g
R_{2}=\dfrac{5g}{\dfrac{\sqrt{3}}{2}-\dfrac{1}{4}}
R_{2}=79.5\text{ N}
Resolve forces horizontally.
R_{2}=0.5R_{1}
0.5R_{1}=79.5\text{ N}
R_{1}=159.1\text{ N}
You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.







