Sine & Cosine Rules
Sine & Cosine Rules Revision
Sine & Cosine Rules
The two rules work for any triangle at all – not just the right angled ones we’d use usual trigonometry for.
Here’s the triangle we’ll be referencing from in this section.
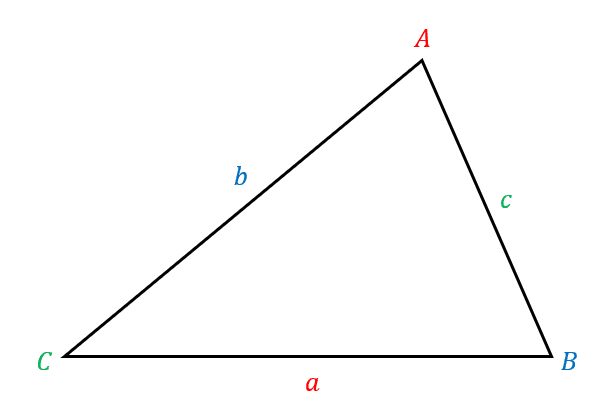
Sine Rule
Use the Sine Rule when you know the values of two angles and one side length, and want to figure out the length of another side.
The rule is
\dfrac{\textcolor{red}{a}}{\sin \textcolor{red}{A}} = \dfrac{\textcolor{blue}{b}}{\sin \textcolor{blue}{B}} = \dfrac{\textcolor{limegreen}{c}}{\sin \textcolor{limegreen}{C}}
Cosine Rule
We’ll use this rule when we know two side lengths and the angle in between. We might also use it when we know all three side lengths.
The rule is
\textcolor{red}{a}^2 = \textcolor{blue}{b}^2 + \textcolor{limegreen}{c}^2 - 2\textcolor{blue}{b}\textcolor{limegreen}{c}\cos \textcolor{red}{A}
Area of Any Triangle
This formula can be used for any pair of sides where the angle in between is also known.
The formula is
\text{Area} = \dfrac{1}{2}\textcolor{red}{a}\textcolor{blue}{b}\sin \textcolor{limegreen}{C}
Note:
If we have two sides and an angle that doesn’t lie in between, we have a bit of a problem.
We’d need to find a little more information out about the system, typically by inspecting the surrounding system.
A Level Maths Predicted Papers 2024
The MME A level maths predicted papers are an excellent way to practise, using authentic exam style questions that are unique to our papers. Our examiners have studied A level maths past papers to develop predicted A level maths exam questions in an authentic exam format. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
A Level Maths Revision Cards
The best A level maths revision cards for AQA, Edexcel, OCR, MEI and WJEC. MME is here to help you prepare effectively for your A Level maths exams. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
Example: Application
Here’s a system of two triangles attached at the side of length \textcolor{red}{5}\text{ cm}.
Find values for x and \alpha.
[4 marks]
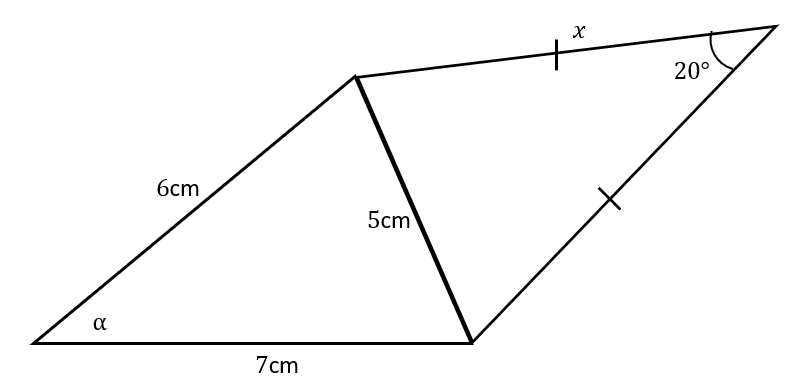
First, let’s solve for x.
Since we know the top triangle is isosceles, the two angles we don’t know yet are equal. Given that the total of angles in the triangle are 180°, we have these two angles as 80° each.
From there
\dfrac{\textcolor{red}{5}}{\sin 20°} = \dfrac{x}{\sin 80°}
so
x = \dfrac{\textcolor{red}{5}\sin 80°}{\sin 20°} = 14.40\text{ cm (to } 2 \text{ dp)}
Now, to solve for \alpha.
\textcolor{red}{5}^2 = \textcolor{blue}{6}^2 + \textcolor{limegreen}{7}^2 - (2 \times \textcolor{blue}{6} \times \textcolor{limegreen}{7} \times \cos \textcolor{red}{\alpha})
or
\textcolor{red}{25} = \textcolor{blue}{36} + \textcolor{limegreen}{49} - 84\cos \textcolor{red}{\alpha}
so
\textcolor{red}{\alpha} = \cos ^{-1}\left( \dfrac{\textcolor{red}{25} - (\textcolor{blue}{36} + \textcolor{limegreen}{49})}{-84}\right) = 44.42°
Sine & Cosine Rules Example Questions
Question 1: Use the cosine rule to find the value of \alpha.
[3 marks]
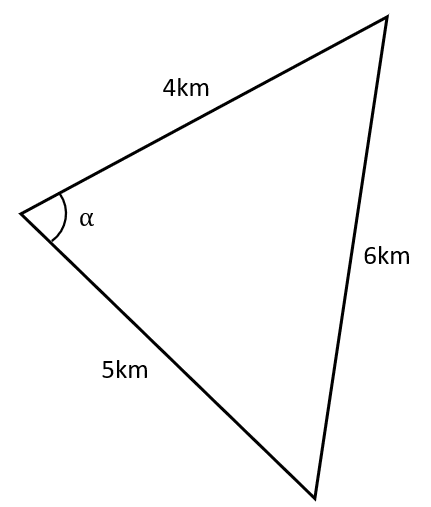
a^2 = b^2 + c^2 - 2bc\cos A
gives
\cos A = \dfrac{b^2 + c^2 - a^2}{2bc}
so
A = \cos ^{-1}\left( \dfrac{b^2 + c^2 - a^2}{2bc}\right) = \cos ^{-1}\left( \dfrac{4^2 + 5^2 - 6^2}{2 \times 4 \times 5}\right) = 82.82°
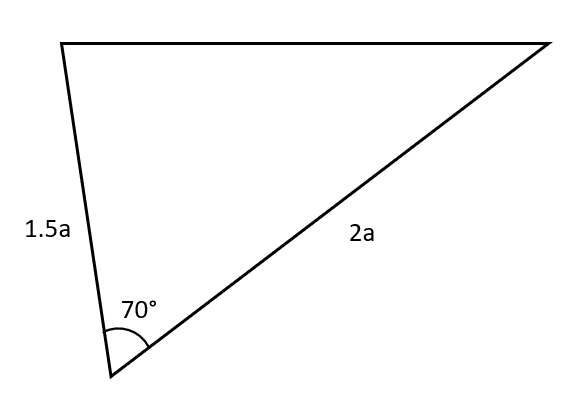
Question 2: For the diagram below, find an expression for the area of the triangle in terms of a.
[2 marks]
Question 3: For the diagram below, find the values of \alpha, \beta and x.
[5 marks]
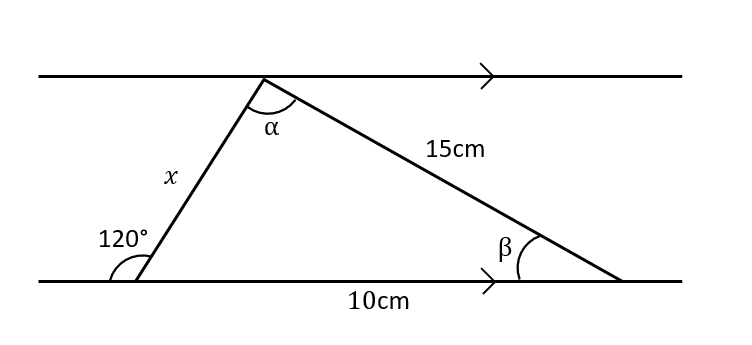
First of all, we have the unmarked angle in the triangle as 180° - 120° = 60°.
By using the sine rule, we have the equation
\dfrac{15}{\sin 60°} = \dfrac{10}{\sin \alpha}
giving
\alpha = 35.26°
Since we have angles in a triangle summing to 180°, we have
\beta = 180° - (60° + 35.26°) = 84.74°
By extension,
\dfrac{15}{\sin 60°} = \dfrac{x}{\sin \beta}
so
x = 17.25\text{ cm (to }2\text{ dp)}
Sine & Cosine Rules Worksheet and Example Questions
Trigonometry
A LevelYou May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.
