The Exponential Function
The Exponential Function Revision
The Exponential Function
We have met exponential functions before, but there is one specific exponential function that has special properties, and it is based around a special number: \color{red}e.
e
The exponential function is \color{red}e^{x}.
\color{red}e=2.71828... is a number. It is a decimal that goes on forever
(like \pi).
\color{red}e^{x} has special properties, most notable being that the gradient of \color{red}e^{x} is \color{red}e^{x}. This will be very important in the differentiation section of the course.
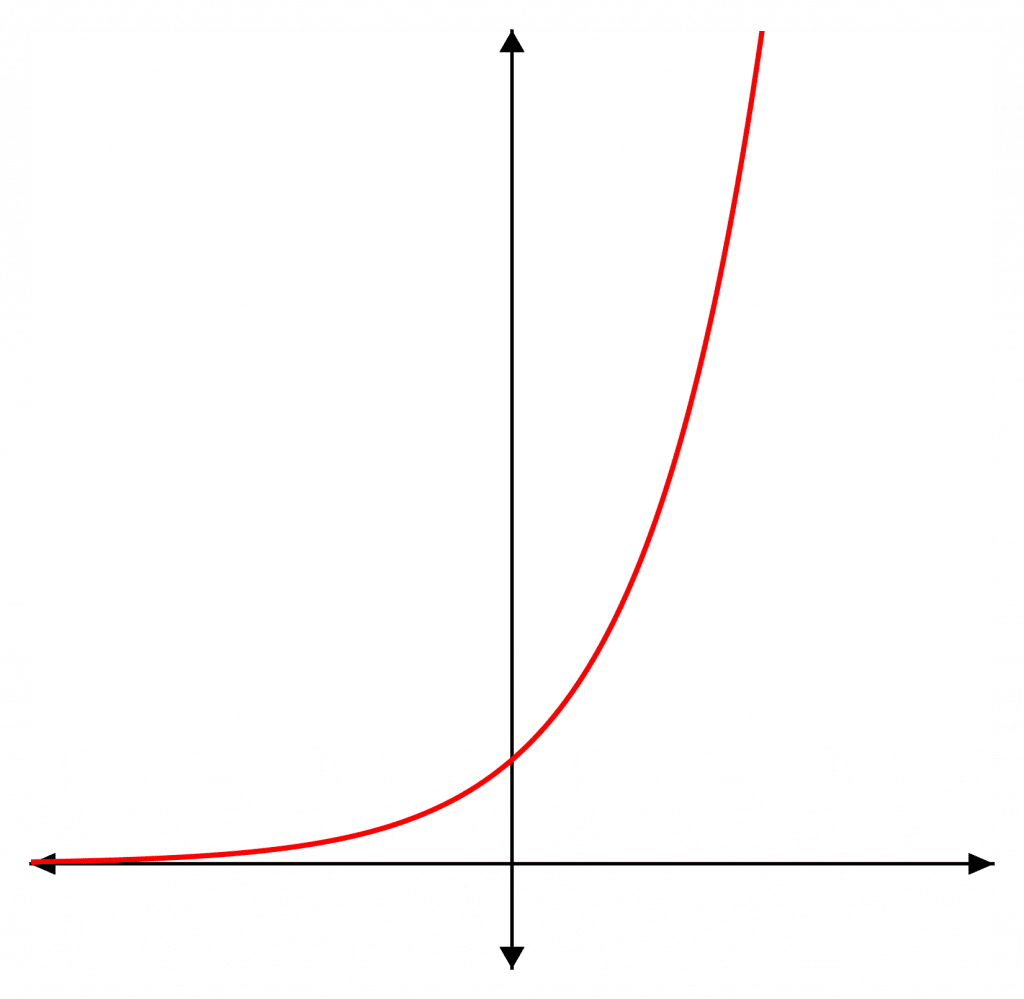
There are some key facts to remember about the graph of y=e^{x}:
- It crosses the y-axis at (0,1)
- As x\rightarrow\infty, \color{red}e^{x}\color{grey}\rightarrow\infty and as x\rightarrow -\infty, \color{red}e^{x}\color{grey}\rightarrow0
- \color{red}e^{x} is never negative.
y=e^{ax+b} + c is a transformation of y = e^x, where a is a horizontal stretch, b moves it horizontally and c moves it vertically.
y = e^{-x} reflects y=e^x in the y-axis.
Natural Logarithm
The inverse function of \color{red}e^{x} is the natural logarithm \color{blue}\ln(x). This is the logarithm with base \color{red}e (\text{log}_e (x)).
All the laws of logarithms can be applied to the natural logarithm.
\color{blue}\ln(a)\color{grey}+\color{blue}\ln(b)\color{grey}=\color{blue}\ln(ab)
\color{blue}\ln(a)\color{grey}-\color{blue}\ln(b)\color{grey}=\color{blue}\ln\left(\dfrac{a}{b}\right)
\color{blue}\ln(a^{b})\color{grey}=\color{blue}b\ln(a)
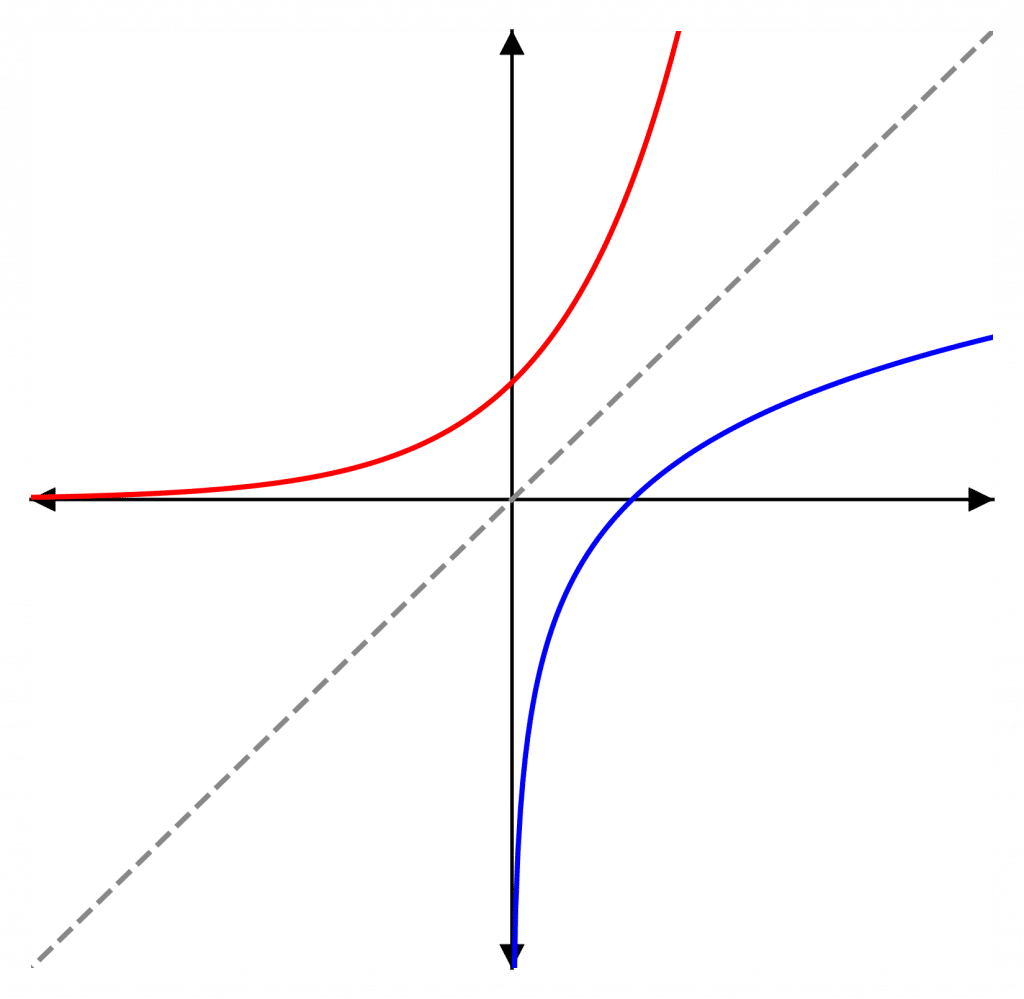
The graph of the natural logarithm (in blue) is the reflection in the line y=x of the graph of the exponential function (in red).
There are key facts to remember about the graph of \color{blue}y=\ln(x):
- It crosses the x-axis at (1,0)
- As x\rightarrow\infty, \color{blue}\ln(x)\color{grey}\rightarrow\infty and as x\rightarrow0, \color{blue}\ln(x)\color{grey}\rightarrow -\infty
- \color{blue}\ln(x) does not take any values for x\leq0
Since \ln (x) is the inverse of e^x and is a logarithmic function, we have these formulas relating the two:
\textcolor{red}{e}^{\textcolor{blue}{\ln (x)}} = x
\textcolor{blue}{\ln} \textcolor{red}{(e^x)} = x
A Level Maths Predicted Papers 2024
The MME A level maths predicted papers are an excellent way to practise, using authentic exam style questions that are unique to our papers. Our examiners have studied A level maths past papers to develop predicted A level maths exam questions in an authentic exam format. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
A Level Maths Revision Cards
The best A level maths revision cards for AQA, Edexcel, OCR, MEI and WJEC. MME is here to help you prepare effectively for your A Level maths exams. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
Example 1: Equations Involving the Exponential Function
Solve for x:
\color{red}e^{3x}\color{grey}=10[2 marks]
\color{red}e^{3x}\color{grey}=10
3x=\color{blue}\ln(10)
\begin{aligned}x&=\dfrac{\color{blue}{\ln(10)}}{3}\\[1.2em]&=0.768\end{aligned}
Example 2: Equations Involving Logarithms
Solve for x:
\color{blue}\ln(4x+3)\color{grey}=2[2 marks]
\color{blue}\ln(4x+3)\color{grey}=2
4x+3=\color{red}{e^{2}}
4x=\color{red}e^{2}\color{grey}-3
\begin{aligned}x&=\dfrac{1}{4}(\color{red}e^{2}\color{grey}-3)\\[1.2em]&=1.10\end{aligned}
The Exponential Function Example Questions
Question 1: Solve for x:
a) e^{x}=2
a) e^{5x}=19
c) e^{12x}=234
[6 marks]
a) e^{x}=2
\begin{aligned}x&=\ln(2)\\[1.2em]&=0.693\end{aligned}
b) e^{5x}=19
5x=\ln(19)
\begin{aligned}x&=\dfrac{1}{5}\ln(19)\\[1.2em]&=0.589\end{aligned}
c) e^{12x}=234
12x=\ln(234)
\begin{aligned}x&=\dfrac{1}{12}\ln(234)\\[1.2em]&=0.455\end{aligned}
Question 2: Solve for x:
a) \ln(x+1)=4
a) \ln(3x+2)=1.5
a) \ln(9x+36)=0.6
[6 marks]
a) \ln(x+1)=4
x+1=e^{4}
\begin{aligned}x&=e^{4}-1\\[1.2em]&=53.6\end{aligned}
b) \ln(3x+2)=1.5
3x+2=e^{1.5}
3x=e^{1.5}-2
\begin{aligned}x&=\dfrac{1}{3}(e^{1.5}-2)\\[1.2em]&=0.827\end{aligned}
c) \ln(9x+36)=0.6
9x+36=e^{0.6}
9x=e^{0.6}-36
\begin{aligned}x&=\dfrac{1}{9}(e^{0.6}-36)\\[1.2em]&=-3.80\end{aligned}
Question 3: Solve for x:
e^{2x}-13e^{x}+36=0[4 marks]
Note that e^{2x}=(e^{x})^{2}
(e^{x})^{2}-13e^{x}+36=0
Substitute: y=e^{x}
y^{2}-13y+36=0
(y-9)(y-4)=0
y=9 or y=4
Reverse substitution:
e^{x}=9 or e^{x}=4
x=\ln(9) or x=\ln(4)
x=2.20 or x=1.39
Question 4: Solve for x:
\ln(4x+3)-2\ln(x)=5[5 marks]
\ln(4x+3)-2\ln(x)=5
\ln(4x+3)-\ln(x^{2})=5
\ln\left(\dfrac{4x+3}{x^{2}}\right)=5
\dfrac{4x+3}{x^{2}}=e^{5}
4x+3=e^{5}x^{2}
e^{5}x^{2}-4x-3=0
Use quadratic formula:
\begin{aligned}x&=\dfrac{-b\pm\sqrt{b^{2}-4ac}}{2a}\\[1.2em]&=\dfrac{4\pm\sqrt{(-4)^{2}-4\times e^{5}\times(-3)}}{2e^{5}}\\[1.2em]&=\dfrac{4\pm\sqrt{16+12e^{5}}}{2e^{5}}\\[1.2em]&=\dfrac{2\pm\sqrt{4+3e^{5}}}{e^{5}}\end{aligned}
x=0.156 or x=-0.129
We can discount the negative solution because \ln(x) is not valid for negative x.
x=0.156
The Exponential Function Worksheet and Example Questions
Exponentials and Natural Logarithms
A LevelYou May Also Like...
MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.
