Trig Equations

A LevelAQAEdexcelOCR

Trig Equations Revision

Trig Equations

Solving the basic trig equations is pretty easy, but what happens if we’ve got a function which has been stretched or translated?

Make sure you are happy with the following topics before continuing.

Trig Graphs

Inspection

First, we need to find an initial solution.

So, for example, let’s say we want to find the values of $x$ when $\textcolor{red}{\tan x} = \textcolor{purple}{\dfrac{1}{\sqrt{3}}}$ .

We want to draw the graph, and mark on a horizontal line where the condition is met, i.e. where $\textcolor{red}{\tan x} = \textcolor{purple}{\dfrac{1}{\sqrt{3}}}$ .

By inspection, we know that the initial solution is at $30°$ , and we can see it repeats at every $180°$ .

We’ll denote this $30° \pm 180°n$ .

Product

A Level Maths Predicted Papers 2024

114

£12.99

The MME A level maths predicted papers are an excellent way to practise, using authentic exam style questions that are unique to our papers. Our examiners have studied A level maths past papers to develop predicted A level maths exam questions in an authentic exam format. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.

View Product

Product

A Level Maths Revision Cards

153

£16.99

The best A level maths revision cards for AQA, Edexcel, OCR, MEI and WJEC. MME is here to help you prepare effectively for your A Level maths exams. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.

View Product

CAST Diagrams

The CAST diagram is a handy tool to show us where values of the standard trig functions are positive.

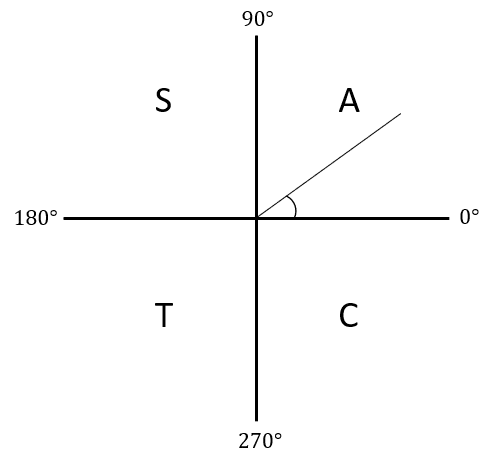
So, here’s the breakdown:

For $0° < x < 90°$ , ALL of $\textcolor{blue}{\sin x}, \textcolor{limegreen}{\cos x}$ and $\textcolor{red}{\tan x}$ are positive
For $90° < x < 180°$ , ONLY $\textcolor{blue}{\sin x}$ is positive
For $180° < x < 270°$ , ONLY $\textcolor{red}{\tan x}$ is positive
For $270° < x < 360°$ , ONLY $\textcolor{limegreen}{\cos x}$ is positive

Think back to plotting the Unit Circle, in the Trig Basics section.

Let’s say we want to find the values of $x$ such that $\textcolor{red}{\tan x} = \textcolor{purple}{\dfrac{1}{\sqrt{3}}}$ , as before.

We know that there is a solution when $x = 30°$ .

First, we plot the point on the diagram, then find the corresponding angles:

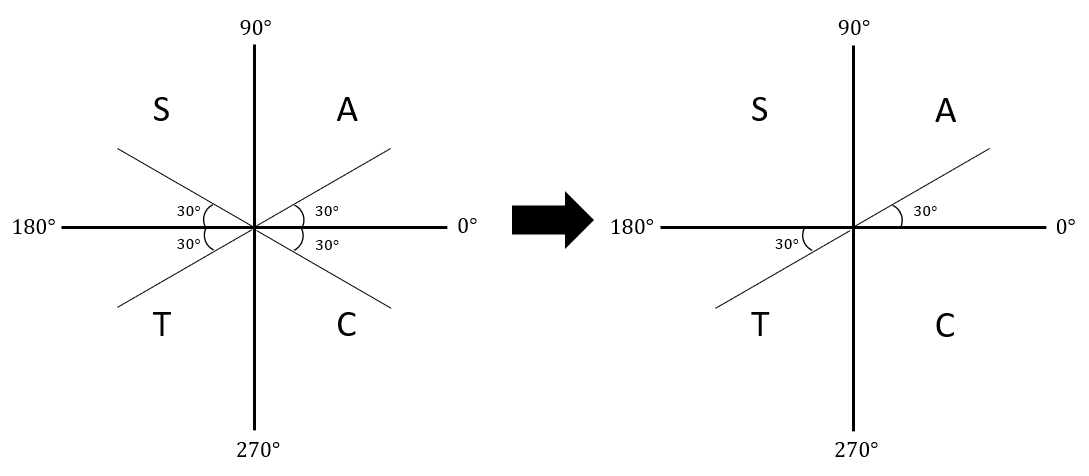
From here, we can see that $\textcolor{red}{\tan x} = \textcolor{purple}{\dfrac{1}{\sqrt{3}}}$ when $x = 30° \pm 360°n$ or $210° \pm 360°n$ , or, more concisely, $30° \pm 180°n$ .

We ignored the two solutions where $\textcolor{red}{\tan x}$ is not positive, i.e. $90° < x < 180°$ and $270° < x < 360°$ .

Dealing With Trig Transformations

Transformations pose a little bit of a problem… See, CAST diagrams become much harder to navigate now. You’re much better off sketching out the function and solving using the horizontal line technique.

So, let’s just begin with an example.

We have $f(x) = \cos 3x$ . Find the values of $x \in \lbrack 0°, 360°\rbrack$ * such that $f(x) = \textcolor{purple}{\dfrac{1}{2}}$ .

* This is just set notation, meaning $0° \leq x \leq 360°$

Well, we have a series of solutions, but they’re not immediately obvious.

What we can do instead is plot the regular $\textcolor{limegreen}{\cos x}$ graph on an interval three times as large as the proposed interval, and divide our solutions there by $3$ .

$\textcolor{limegreen}{\cos x} = \textcolor{purple}{\dfrac{1}{2}}$ has solutions $60°, 300°, 420°, 660°, 780°, 1020°$ .

Therefore, $\cos 3x = \textcolor{purple}{\dfrac{1}{2}}$ has solutions $20°, 100°, 140°, 220°, 260°, 340°$ .

Trig Equations Example Questions

Question 1: Sketch the $\sin x$ graph and by inspection, find the solutions of $\sin x = \dfrac{-\sqrt{3}}{2}$ , in the interval $-360° \leq x \leq 360°$ .

[2 marks]

$x = \sin ^{-1} \left( \dfrac{\sqrt{3}}{2}\right) = -120°, -60°, 240°, 300°$

Question 2: Using a CAST diagram, find the values of $x$ such that $\cos x = 0.2588$ .

[2 marks]

$\cos x = 0.2588$ gives $x = 75°$ .

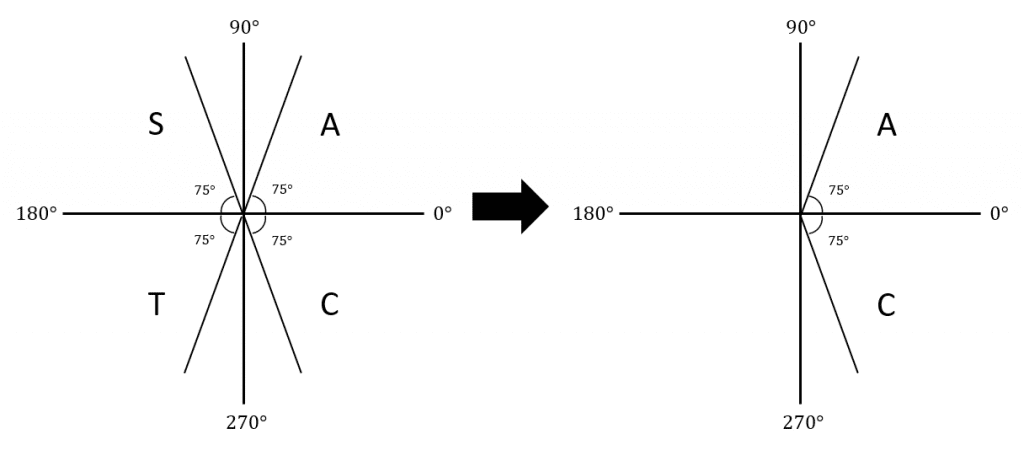By the CAST diagram, we can see that we also have a solution where $x = 270° + 15° = 285°$ .

Question 3: For $f(x) = 2\sin \dfrac{3x}{2}$ , find the values of $x \in \lbrack -2\pi, 2\pi \rbrack$ where $f(x) = 1$ .

[4 marks]

For $f(x) = 1$ , we want $\sin \dfrac{3x}{2} = \dfrac{1}{2}$ .

If we look for values of $-3\pi \leq x \leq 3\pi$ where $\sin x = \dfrac{1}{2}$ , and multiply our values of $x$ by a scale factor of $\dfrac{2}{3}$ , we have our new set of solutions.

$\sin x = \dfrac{1}{2}$ occurs at $\dfrac{-11\pi}{6}, \dfrac{-7\pi}{6}, \dfrac{\pi}{6}, \dfrac{5\pi}{6}, \dfrac{13\pi}{6}, \dfrac{17\pi}{6}$

Therefore the solution of $f(x) = 1$ is $x = \dfrac{-11\pi}{9}, \dfrac{-7\pi}{9}, \dfrac{\pi}{9}, \dfrac{5\pi}{9}, \dfrac{13\pi}{9}, \dfrac{17\pi}{9}$ .