Shop
GCSE Maths Revision Cards
GCSE Maths Revision Cards
Revise for your GCSE maths exam using the most comprehensive maths revision cards available. These GCSE Maths revision cards are relevant for all major exam boards including AQA, OCR, Edexcel and WJEC. The profit from every pack is reinvested into making free content on MME. Learn more today with the MME GCSE Maths flashcards.
-
Free Shipping Included!
-
All of the GCSE maths topics covered - Higher and foundation available
-
Suitable for the 23/24 academic year - Best rated revision cards
-
Practice questions and answers on every topic
-
Over 80 flashcards for foundation and over 90 flashcards for higher
Got a question?
We'd love to talk about how we can help you.
How they look
Get a sneak peak of one card from each of the 7 topics in our exceptional GCSE Maths flashcard pack.
GCSE Maths flashcards - Summarise key concepts
Our GCSE Maths revision cards have been designed to effectively condense all essential concepts you need to know for the exam, in an easy to remember format, thereby helping you increase the volume of knowledge you retain. These flash cards also make it easy to cover all the key areas of the course in double-quick time.
-
Quickly identify areas that you need to revise in more depth.
-
Exam style questions on the back of each card
-
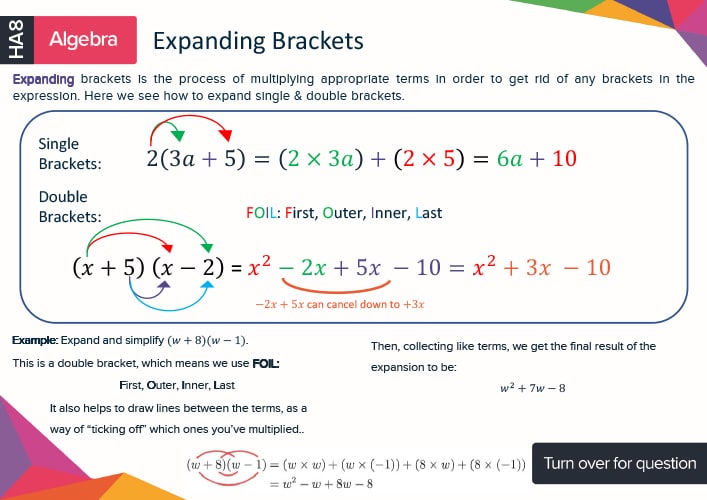
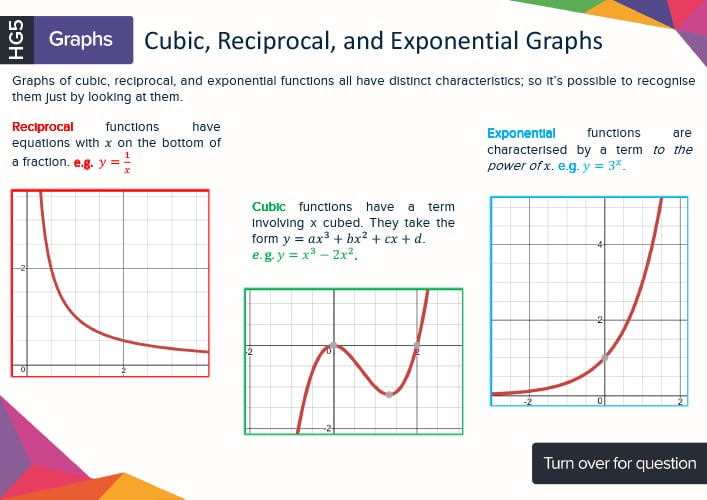
Detailed diagrams explaining each topic
-
Colour coded sections for must-know information

GCSE Maths flashcards - An effective way to revise
Revision flash cards are one of the classic study tools, and for good reason – they promote studying through active recall, which is one of the practices through which our brains learn most effectively. The MME revision pack has even more content than CorbettMaths Cards, CGP flashcards or any other GCSE maths revision cards.
-
All major topics covered - Number, Algebra, Graphs, Ratio, Proportion, Geometry, Trigonometry, Stats, Probability and more.
-
Higher and foundation - When you purchase the cards, opt for either a foundation or higher pack.
-
Key formulas - Memorise the GCSE maths formulae essential for your exam
-
GCSE maths revision cards in flashcard format!

Foundation Card Topics Covered
All of the topics in the GCSE maths curriculum are covered the GCSE Maths Revision Cards pack.
Higher Card Topics Covered
GCSE Maths Revision Cards
Frequently Asked Questions
Any questions you have about our GCSE Maths Revision Cards are answered here.
Simply click any buy now button on this page, then select which pack of cards you want, and add to your cart. Follow the checkout process to complete your order.
Yes, the topics covered in the maths packs are all the key areas of the GCSE maths curriculum.
There are 91 higher GCSE maths cards and 81 foundation cards in each pack.
We use Royal Mail to ensure all orders arrive safely and on time. With all standard orders the average shipping time is 2-3 working days.
They come in a pack and are ordered by topic, with each card titled for easy identification.
Yes we have online answers for every question asked and we also have a range of revision worksheets that are freely accessible on our GCSE maths revision page.
GCSE Maths Revision Card Answers
Use the button below to view the answers to the GCSE maths cards

Shipping / Delivery Information
All items are shipped using Royal Mail. For our standard shipping option, this means you should receive your items within 2-3 working days for all UK orders. International shipping varies depending on the country but usually takes between 5-10 working days.
| Item | United Kingdom | Europe | Rest of World |
|---|---|---|---|
| Orders Under £40 | Royal Mail (3-4 Working days): £1.99 Royal Mail 24 (1-2 working days): £4.99 |
Europe Shipping:£19.99 | Varies |
| Orders Over £40 | Free UK shipping (3-4 Working days) Royal Mail 24 (1-2 working days): £4.99 |
Europe Shipping:£19.99 | Varies |
Bulk Discounts for Schools
MME offers bulk discount for schools/colleges and training providers, as well as a dedicated mock paper printing service. Check out the pricing below and place an order using the order form below. Alternatively, fill in the contact form to request more information.
Price List
Order Form
Rating breakdown
-
5 stars236
-
4 stars16
-
3 stars16
-
2 stars2
-
1 stars0
Highly rated for:
of customers recommend this product
You May Also Like...
Secure Shopping at MME
All payment details you send us are shielded via SSL encryption.

Ways to Pay
We accept all major credit / debit cards, PayPal, Apple Pay & Google Pay.
Helping you buy
Having trouble? Call our customer support team:
020 3633 5145
Need it quicker?
Place your order before 2pm and select Next Working Day delivery at checkout.
























The MME GCSE maths revision cards are ideal. We had them last year for our younger one and then we got a new set this time as the ones we previously got were well used to say the least. Good delivery and service good all round
The cards were fine
As a tutor, I buy several of these a year, the students think they are brilliant and it always provides a green/red area for the subject on what we need to work on, so yeah ! Top Product
I purchased these for my daughter who has been using them before and after lessons at school to help with recapping. She struggles to concentrate in lesson so having something to look at before and refer back to in a quick way is helping her to retain more information. Her overall understanding is definitely improving. As they say it is the small sustainable changes you make that make all the difference and we are certainly seeing this
Very pleased with the gcse maths cards. They look nice and have all the info for each subject.
Used the mme website for a number of years with my private students for tutoring. I have recommended that they all buy the GCSE maths cards as they are a great way to check knowledge on a topic quickly as well as having the entire spec in the palm of your hand. I tend to use them at the start and end of each session to introduce a topic and recap.
5 star maths revision cards. Whoop!
there are 2 lots of GCSE maths revision cards I have. One that school gave and this set that my parents got. There is no comparison, the mme cards are way better and explain everything in an easy format.
thank you MME for all the great website resources. I have just tried out these cards and if anything the content is better than what is on the site, or maybe you do tjhat on purpose to get more people to buy
Awesome set of maths flashcards that really helped me to get to grips with algebra at last