2D Shapes and Quadrilaterals
2D Shapes and Quadrilaterals Revision
2D Shapes
A polygon is a shape made up of straight edges.
There are two types of polygons you need to know about:
- Regular – All sides and angles are the same
- Irregular – All sides and angles are not the same
Regular Polygons
You will already be familiar with the names of some shapes, but it’s important to recognise the names of shapes that have up to 10-sides, as seen below.
All the shapes below are regular polygons, meaning all the sides in one shape are the same length.
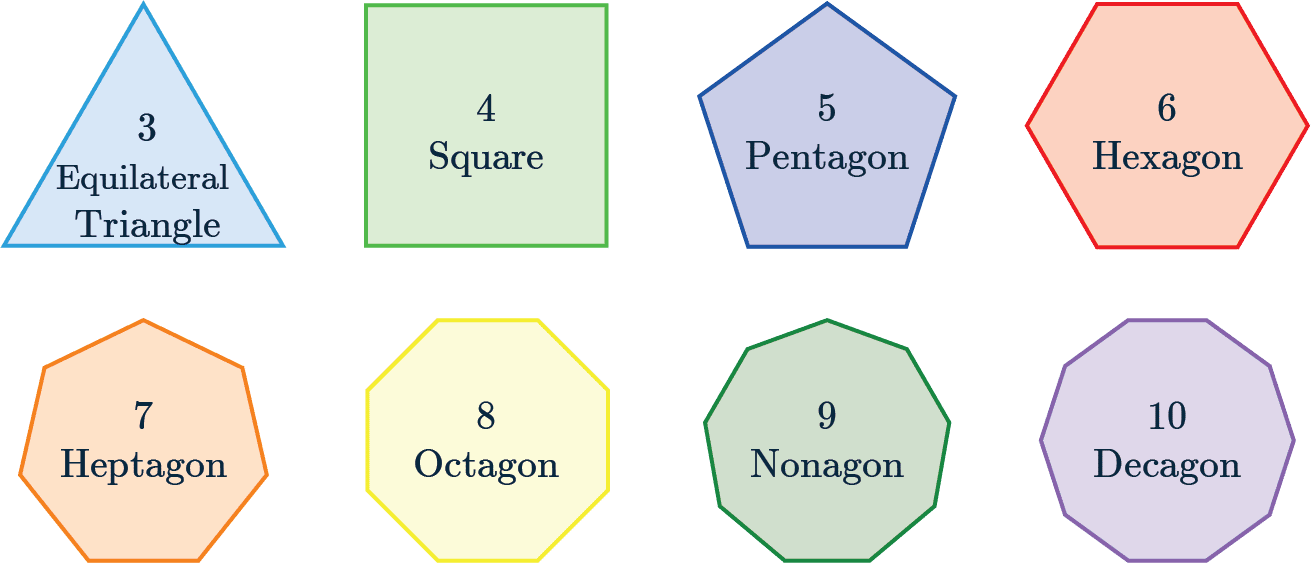
All of these shapes are regular polygons, meaning that all of their sides are the same length and all the angles are the same.
Irregular polygons
Look at the irregular shapes shown:
Shape A – Counting the number of sides, we see that shape \textcolor{red}{A} has 4 sides, therefore it is a quadrilateral.
Shape B – Doing the same for \textcolor{blue}{B}, we see that it has 7 sides, and therefore it is a heptagon.

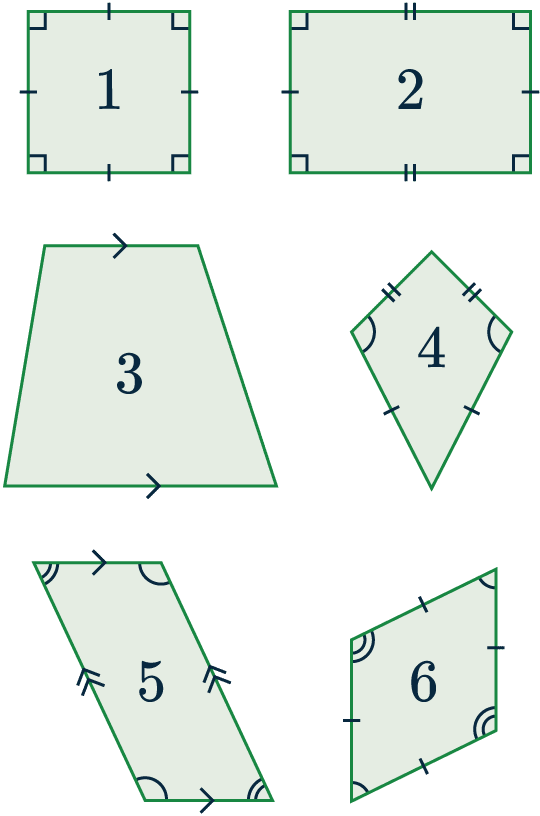
Quadrilaterals: 6 Common Types
Triangles and quadrilaterals are the shapes we will see most often. As a result, we have names for specific types of them.
The different types of quadrilaterals you should be familiar with are:

1. Square – Has 4 sides equal in length, and 4 equal angles (all 90\degree).
2. Rectangle – Has 4 equal angles (all 90\degree), and its opposite sides are equal in length.
3. Trapezium – Has one pair of parallel sides.
4. Kite – Has two pairs of equal sides, and each pair must be adjacent to each other. Additionally, two of its angles (as marked on the picture) are equal.
5. Parallelogram – Has two pairs of parallel sides. Additionally, opposite angles are equal and adjacent angles add to 180\degree.
6. Rhombus – Has 4 sides equal in length. Additionally, opposite angles are equal, and opposite sides are parallel.
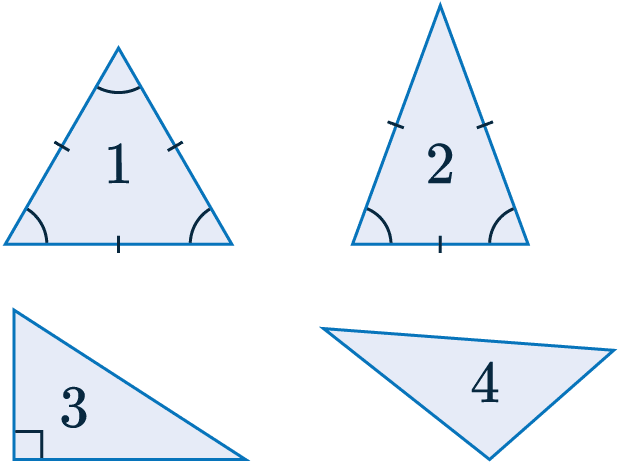
Triangles:
The different types of triangles you should be familiar with are:

1. Equilateral – Has 3 sides equal in length, and all 3 angles are 60\degree.
2. Isosceles – Has 2 sides equal in length, and the two base angles are equal.
3. Right-angled – Has 1 angle equal to 90\degree.
4. Scalene – Has 3 sides of different lengths, and no angles are the same.
2D Shapes and Quadrilaterals Example Questions
Question 1: State the name of the shape below.
[1 mark]

This shape has 5 sides, so it is an irregular pentagon.
Question 2: ABCD is a quadrilateral. AB is parallel to CD. State which type of quadrilateral ABCD is.
[1 mark]
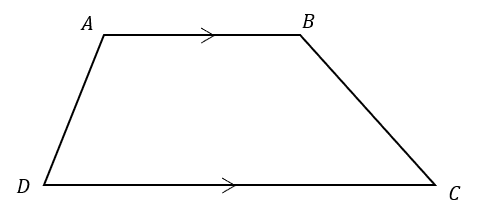
The only feature this quadrilateral has is one pair of parallel sides. Therefore, it must be a trapezium.
Question 3: ABCD is a parallelogram. Angle ABC is 56\degree. Calculate the size of angle x.
[2 marks]

In a parallelogram, adjacent angles add to 180\degree, and angle x is adjacent to ABC, so we get that
x\degree=180\degree-56\degree=124\degree
2D Shapes and Quadrilaterals Worksheet and Example Questions
(NEW) 2D Shapes and Quadrilaterals Exam Style Questions - MME
Level 1-3NewOfficial MME
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now





