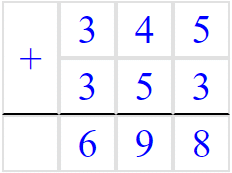
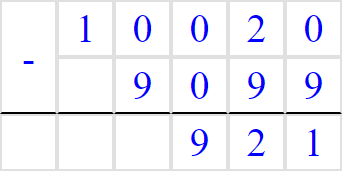
Addition and Subtraction
Addition and Subtraction Revision
Addition and Subtraction
Here we will look at using the column method for adding and subtracting big numbers. This is a fundamental skill for all mathematics.
Skill 1: Addition
The idea behind the column method of addition is firstly adding the ones, then the tens, then the hundreds and so on. Here’s an example broken down into five steps.
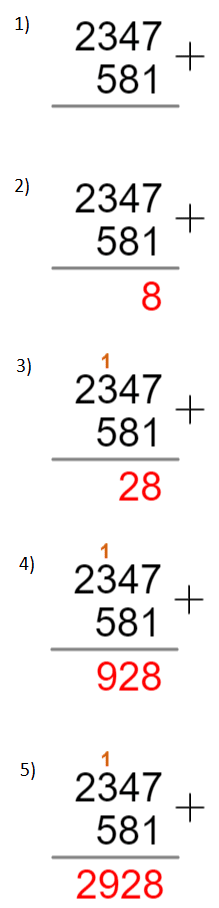
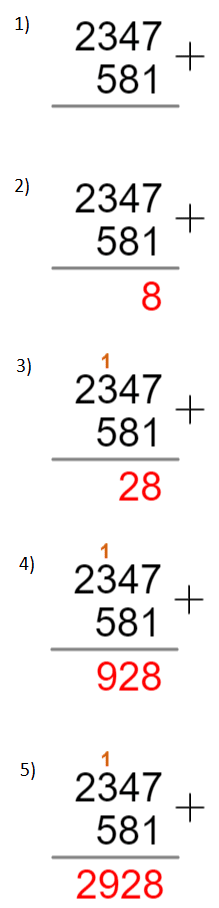
Example: Use the column method to find the result of 2,347 + 581.
1) Firstly, write both the numbers one above the other, making sure the ones line up, the tens line up, and so on. Then, draw a line underneath the numbers.
2) Then, we add the ones column,
7+1=8
And write the result underneath the ones column.
3) Then, add the tens,
4+8=12
Now, since the result is a two-digit number, don’t write the whole thing below the line – we want to carry the 1, which means we write the 2 below the line in the tens column and write the 1 above the hundreds column (technically, it is a hundred).
4) Now, when adding the next column (the hundreds) make sure to add the extra 1 that we obtained:
1+3+5=9
Write the results underneath the hundreds column.
5) Finally, since there is only one value in the next column, we simply write that value underneath the line (you can think of 581 as 0581 and add 0 to 2 if it helps).
Then, once there are no more columns left, your answer will be the number underneath the line.
Skill 2: Subtraction
The column method for subtraction is similar in principle to that for addition – start with the values in the “ones” column on the right and move left – but there are a couple of small differences.
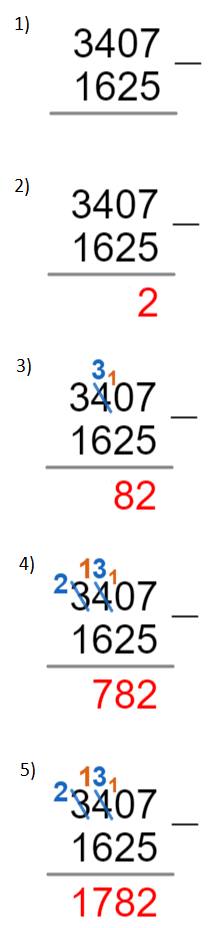
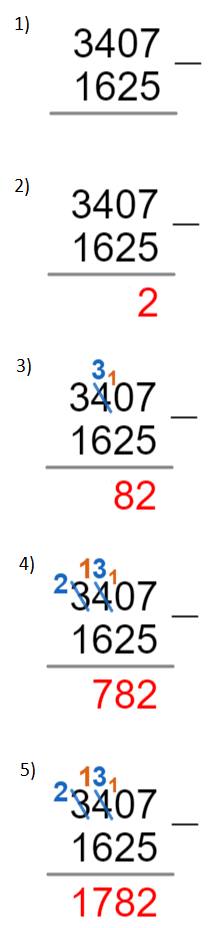
Example: Use to the column method to evaluate 3,407 - 1,625.
1) Firstly, write both the numbers one above the other, making sure the ones line up, the tens line up, and so on. Then, draw a line underneath the numbers.
2) Then, we subtract the ones column,
7-5=2
And write the result underneath the ones column.
3) Then, we want to subtract the tens but that would give us a negative number. So, instead we “borrow” a 1 from the next column along. So, the 0 becomes a 10 and the 4 is reduced to a 3. Then, do the subtraction:
10-2=8
Write the result underneath the tens column.
4) Now, we want to subtract the hundreds but run into the same problem as in step 3), so we borrow a 1 so that in the hundreds column: 3 becomes 13, and in the thousands, 3 is reduced to 2. Then, do the subtraction:
13 - 6 = 7
Write the result underneath the hundreds column.
5) Lastly, subtract the two values in the thousands column:
2-1=1
Write the result underneath the thousands column.
Then, once there are no more columns left, your answer will be the number underneath the line.
Notes:
• If you need to subtract a big number from a smaller (as in, you expect to get a negative answer), do the column method with the bigger number on top and then simply stick a minus sign in front of your answer.
• If you need to borrow a 1 but the next digit along is a zero, then reduce the zero to a 9. Then look to the next digit along and borrow the 1 from it as well (meaning you then have to reduce that digit by 1, as well the other digit you just reduced). You can keep borrowing from the digit to the left until you run out of digits!
Addition and Subtraction Example Questions
Question 1: Using the column method, evaluate 590 + 4,455
[1 mark]
A correct application of the column method should look something like

Therefore, the solution is
4,455+590=5,045
Question 2: Using the column method, evaluate 1,105 - 822
[1 mark]
A correct application of the column method should look something like
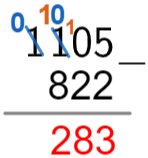
Therefore, the solution is
1,105-822=283
Question 3: Using the column method, evaluate 345 + 353
[1 mark]
Question 4: Using the column method, evaluate 10020 - 9099
[1 mark]
Question 5: Using the column method, evaluate 991 - 1293
[1 mark]
Here we can see the second number is larger, meaning our answer will be minus.
Here we write the second number over the first number:
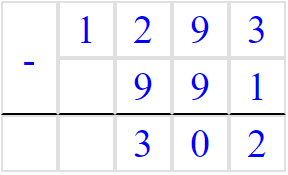
We then perform the subtraction.
1293 - 991 = 302
lastly we add a minus sign to our answer
991 - 1293= - 302