Bar Graphs
Bar Graphs Revision
Bar Graphs
A bar graph (or bar chart) is a way of displaying data, typically data split into categories, using bars of different heights. Bar graphs are not the same thing as histograms, and you should make sure to leave gaps between the bars when drawing your bar graph so it doesn’t look like a histogram. You may also see vertical line charts. These do the same thing as bar charts, but a vertical line is used instead of a bar.
Understanding the following topics will help with bar graph questions:
- Frequency tables is essential for this topic
- Fractions, decimals and percentages
How to Draw a Bar Graph
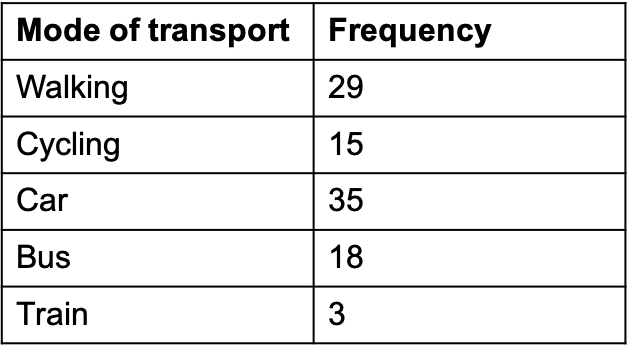

100 students were asked what their primary mode of transport for getting to school was. The results of this survey are recorded in the table below. Construct a bar graph representing this information.
So, before drawing the bar graph, we have to consider what the requirements of our graph will be from the info in the table:
- There are 5 categories, so it must be wide enough for 5 bars,
- The highest frequency is 35, meaning the scale on the y-axis must go at least at as high as 35.
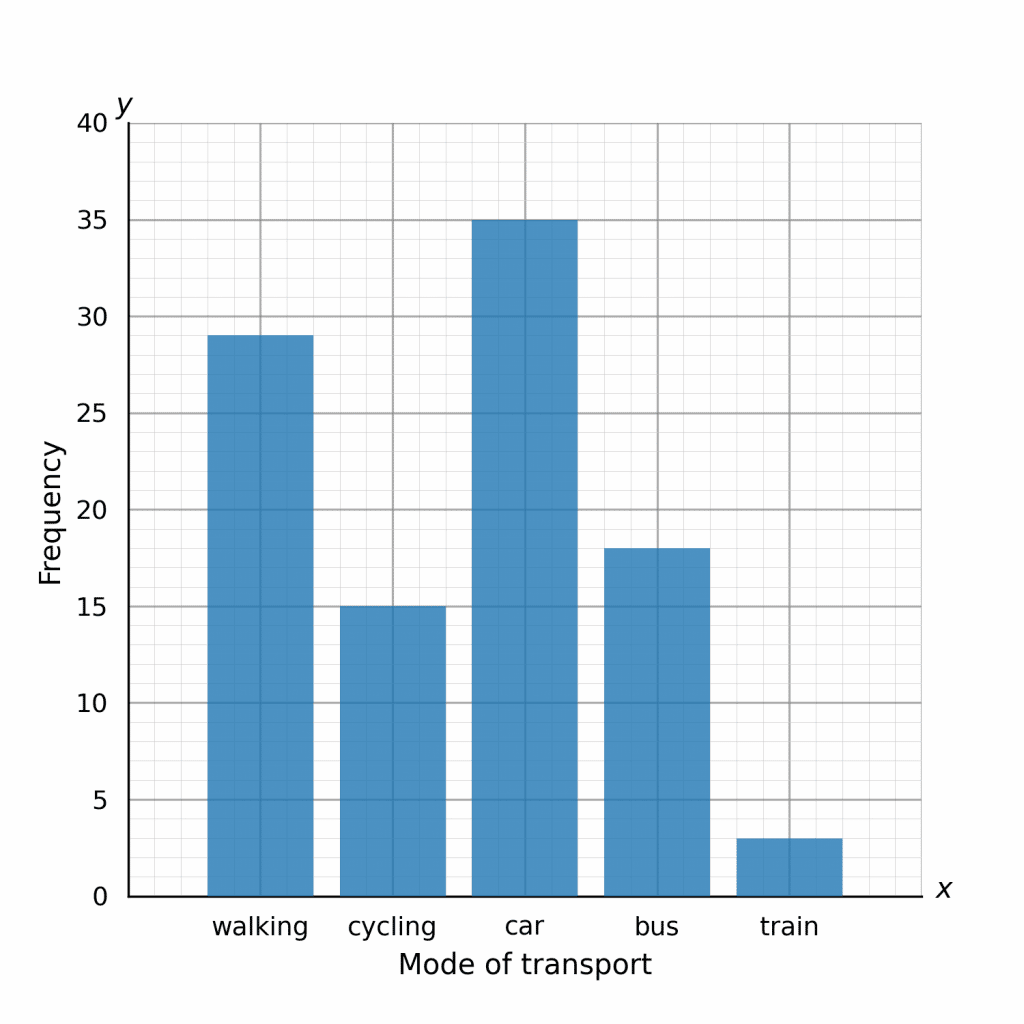

Now, remembering to leave gaps between the bars and clearly labelling which bar represents which mode of transport, the resulting bar graph should look like the one shown.
As you can see, this bar graph displays the information in a clear and obvious way. The bar graph has the following features:
- The bars are very distinct, clearly labelled and have gaps.
- The scale on the y-axis is very readable: 1 small square represents 1 person.
- The scale chosen is appropriate to the data we were given.
- Both axes are labelled.
Understanding Bar Graphs
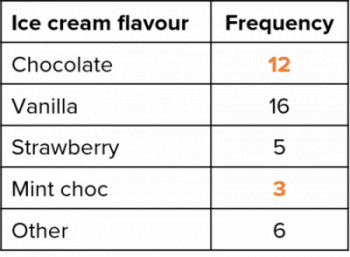
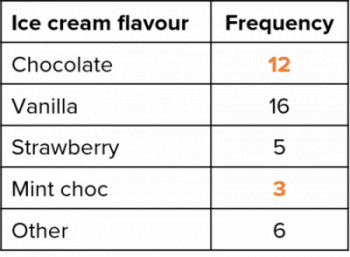
A survey was conducted asking people about their favourite flavour of ice cream. The results of this survey are displayed on the bar chart.
a) Use the bar graph to fill in the gaps in the table.
To fill in the missing gaps in the table, we must read off the height of their corresponding bars from the bar chart.
We can see that each little square is worth 0.6, and so the height of the ‘chocolate’ bar is 12 and the height of the ‘mint choc chip’ bar is 3.
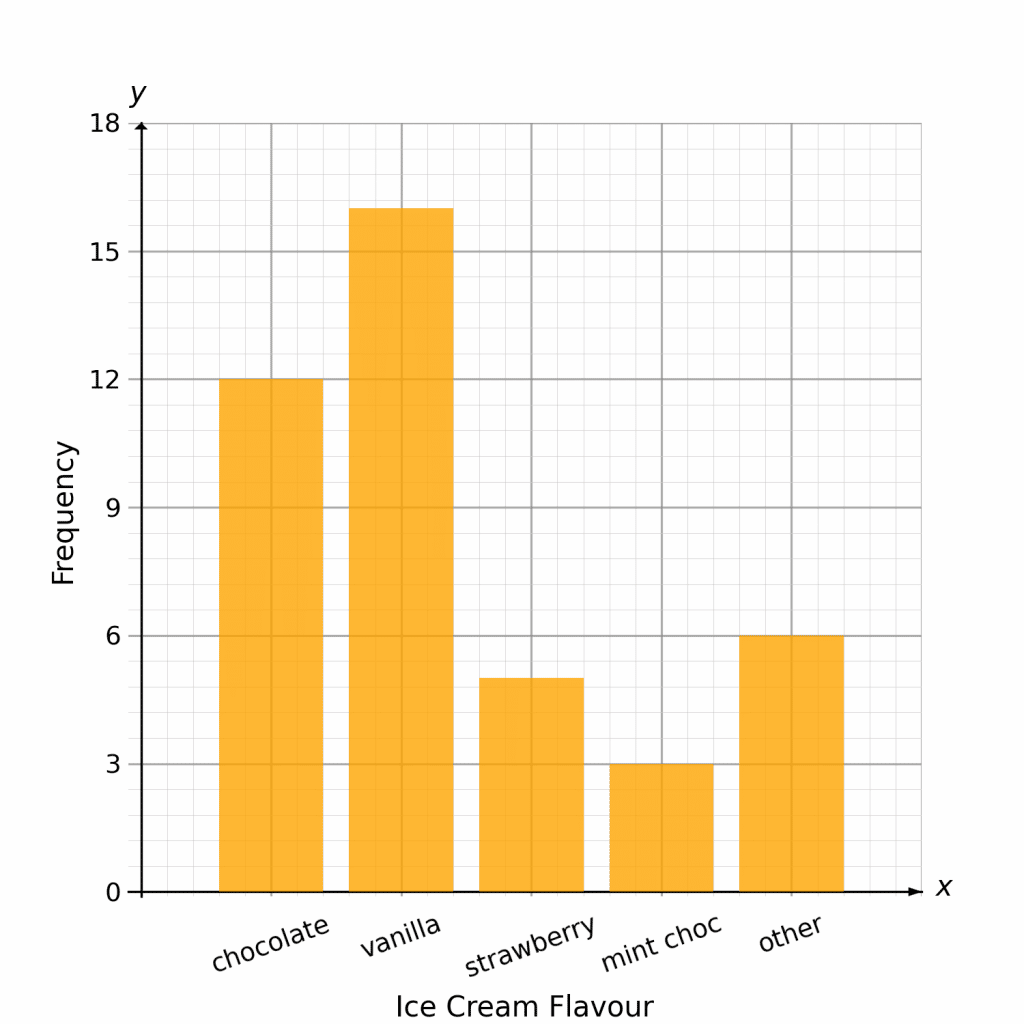
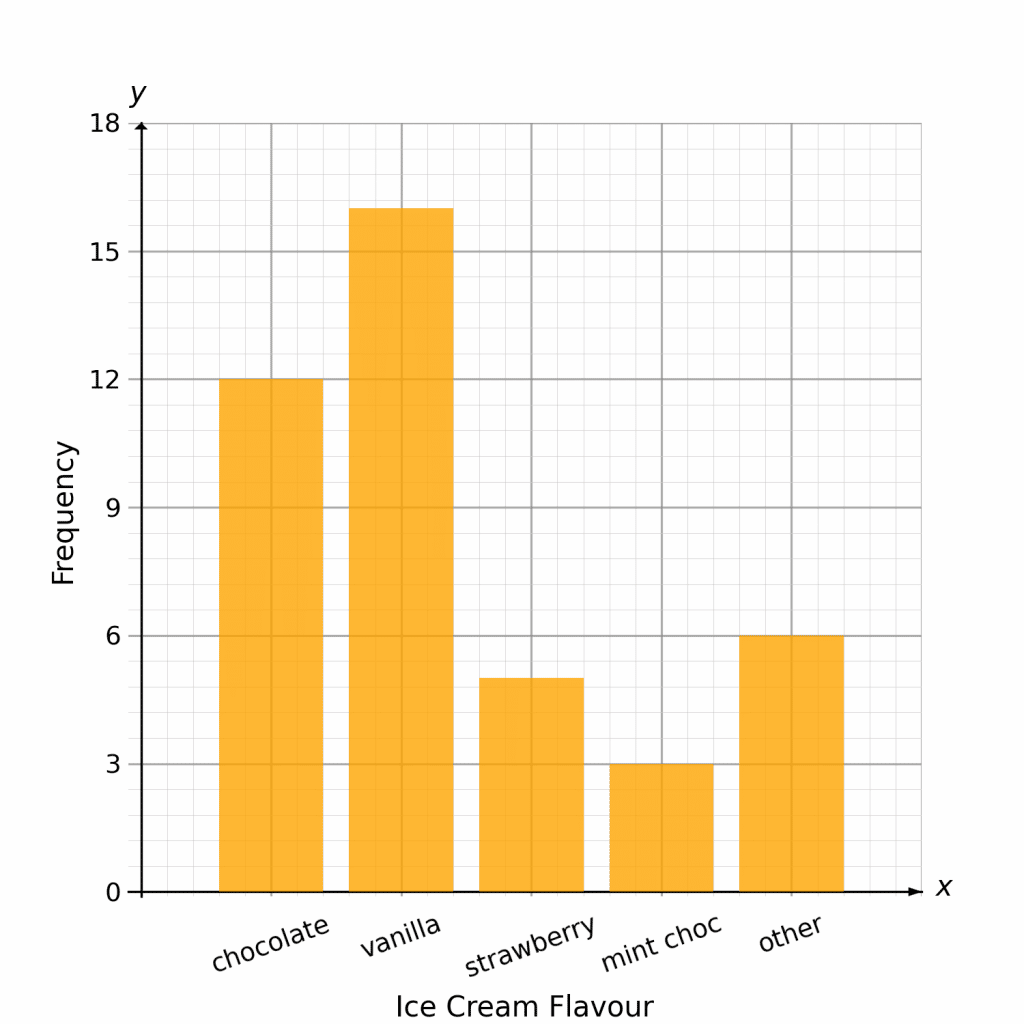
b) Calculate the percentage of people surveyed whose favourite flavour is strawberry.
From the table, we can clearly see that 5 people chose strawberry as their favourite. To find out what this is as a percentage, we need to work out how many people there were in total.
\text{Total }=12+16+5+3+6=42
Therefore, the percentage of people who chose strawberry is
\dfrac{5}{42}\times 100=11.9\%\text{ (1 dp)}
Comparing Data Using Bar Graphs
If we want to compare two sets of data within the same context we can either plot both bar charts on the same graph or plot a composite bar chart.
Side by Side
The following bar chart shows the favourite school subjects of pupils in class 10\text{A} and 10\text{B}.
We are then able to draw conclusions from the bar chart, e.g. English is more popular in class 10\text{B}.
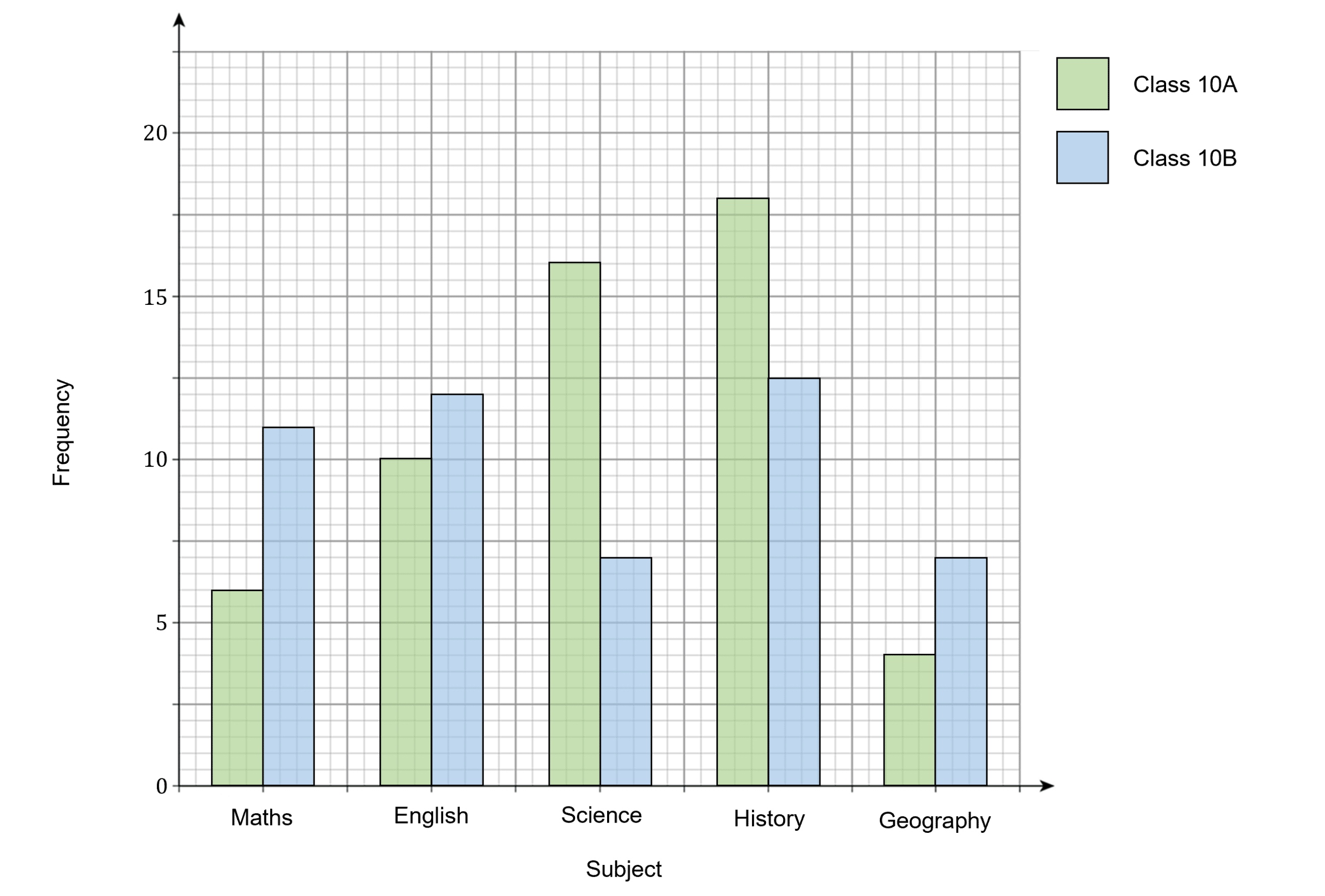
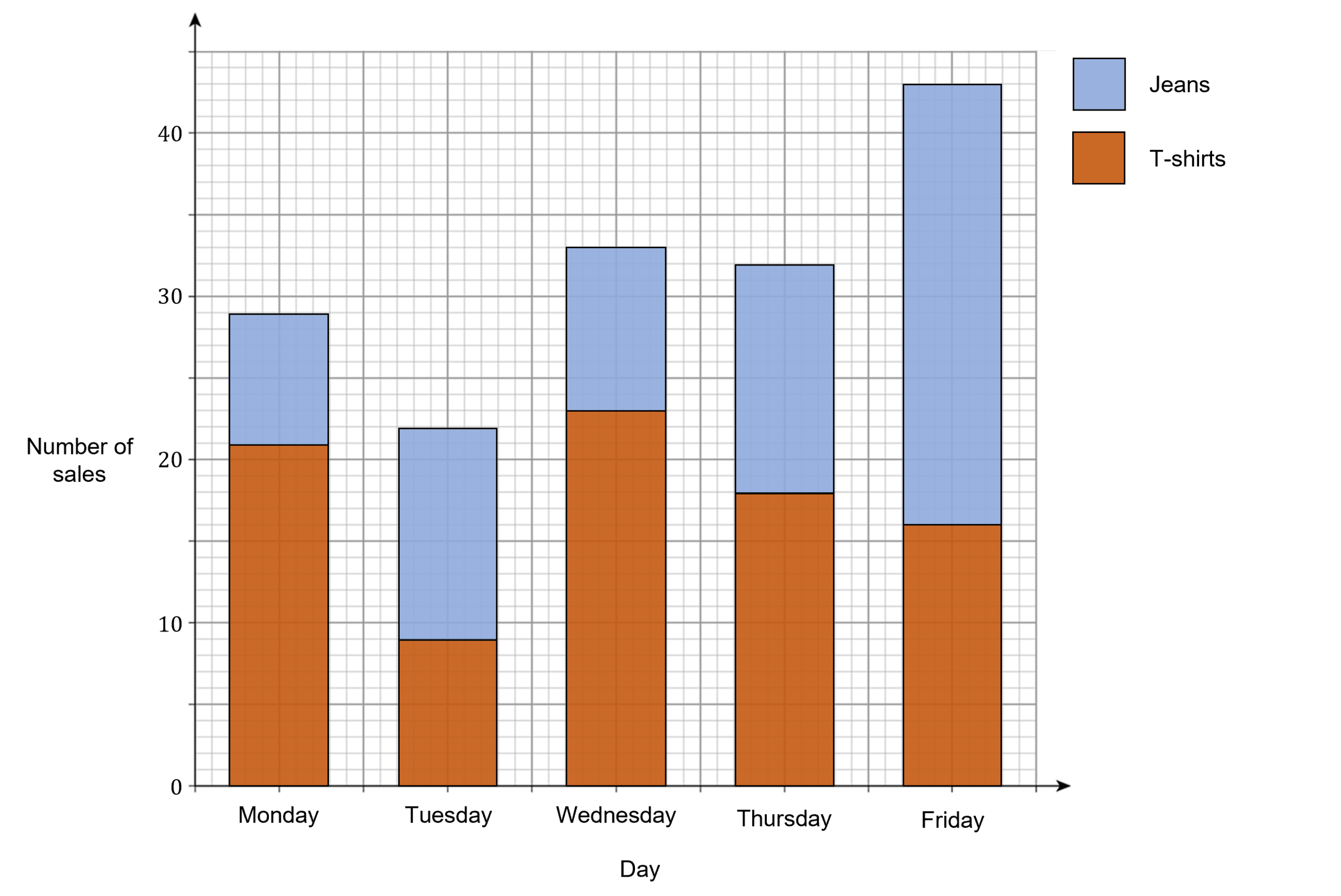
Composite Bar Charts
Composite bar charts are another way of displaying more than one data set within the same context. Instead of the bars being side by side, they are stacked on top of each other.
For example, the bar chart below shows the number of sales at a clothes shop per day for both jeans and t-shirts.
We can see that on Monday there were \textcolor{#10a6f3}{21} t-shirts sold and \textcolor{#10a6f3}{8} pairs of jeans sold.
Bar Graphs Example Questions
Question 1: A survey asked people what their favourite thing to spread on toast was. The results are shown in the table below. Construct a bar graph on the axes below to display the information given in the table.
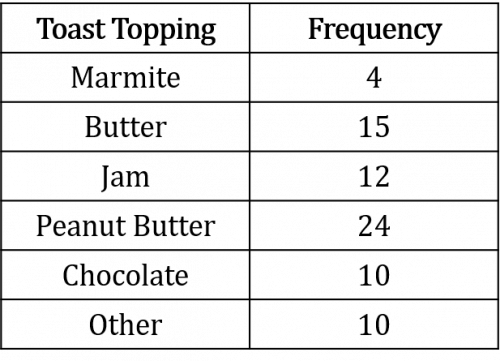
[3 marks]
Your bar graph should look like the one shown below. Remember, you must have gaps between the bars and everything (including the axes and the individual bars) should be clearly labelled.
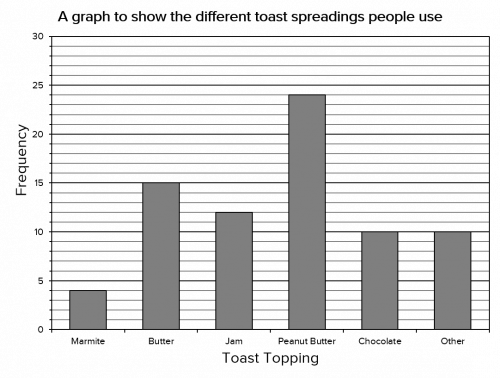
Question 2: A bookstore sells three different kinds of books: paperbacks, hardbacks and audio-books. They record their sales of each type of book over the course of one year and display the results in the bar chart shown below:
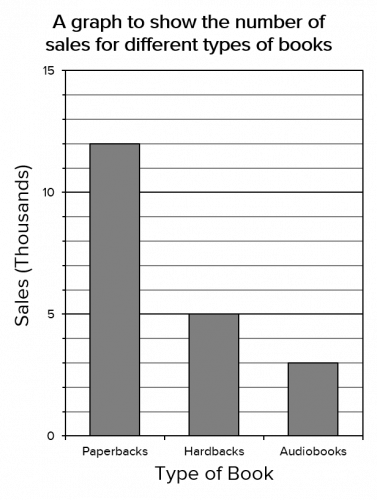
a) What percentage of total book sales were audio-books?
[2 marks]
b) Write the ratio of hardbacks sold to paperbacks sold in its simplest form.
[1 mark]
a) According to the scale on the y-axis, 5 small squares accounts for 2,000 book sales, so:
\text{One small square }=2,000\div 5=400\text{ books}
So, that means the number of audiobooks sold is 3,000, the number of hardbacks sold is 5,000, and the number of paperbacks sold is 12,000. Therefore the percentage of sales that were audiobooks is:
\dfrac{3,000}{3,000+5,000+12,000}\times 100=15\%
b) We’ve already determined the number of hardbacks and paperbacks sold, so the ratio is:
5,000 : 12,000 = 5 : 12
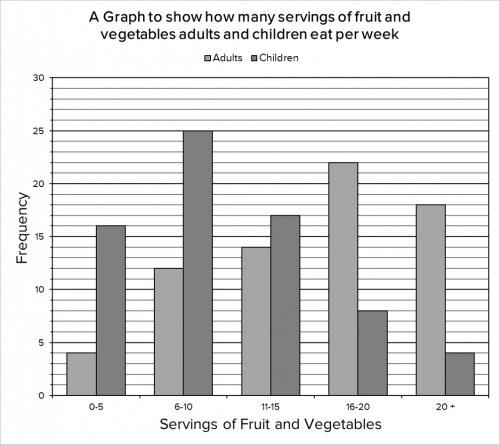
Question 3: 70 adults and 70 children were surveyed to find out how many servings of fruit and vegetables they eat per week. The results are shown in the bar graph below:
a) How many adults and children combined eat between 0 and 5 servings of fruit and vegetables per week?
[1 mark]
b) What is the difference between the number of children who eat over 20 servings of fruit and vegetables per week and between 6 to 10 servings of fruit and vegetables per week?
[1 mark]
c) What is the mode for the number of servings of fruit and vegetables eaten per week by adults?
[1 mark]
d) What basic trend do we notice from the data presented?
[1 mark]
a) For this question, we need to take a reading of the two bars showing the 0 – 5 servings per week category. The number of adults who have between 0 and 5 servings per week is a total of 4. The number of children who have between 0 and 5 servings per week is a total of 16.
Therefore, the number of adults and children combined who have between 0 and 5 servings is 4+16 = 20
b) For this question, we simply need to locate the bar that represents children eating over 20 servings and the bar that represents children eating between 6 – 10 servings, and work out the difference between them.
The number of children who eat over 20 servings of fruit and vegetables is 4. The number of children who eat between 6 and 10 servings of fruit and vegetables is 25. Therefore, the difference between these two categories is 25-4=21
c) The mode is the most frequently occurring value. Since this question is about the adults, we do not need to consider the bars for children. All we need to do is see which bar is highest for the adults.
The 16 – 20 bar is the highest with 22 (the actual number 22 doesn’t really need to be considered since we can clearly see that the bar contains the most values since it is obviously higher than the other adult bars). Therefore the mode is 16 – 20 servings.
d) The most basic trend we can obtain from the given information is that adults eat more portions of fruit and vegetables per week than children.
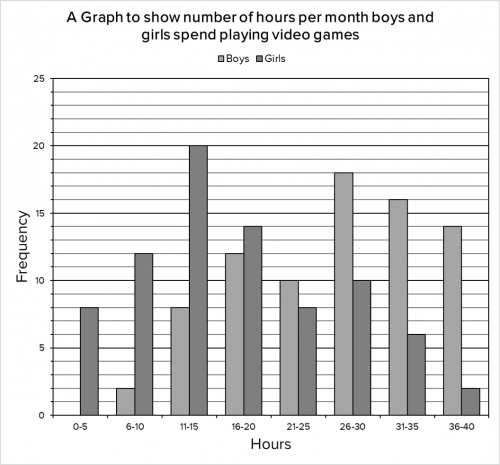
Question 4: A survey was conducted on the number of hours per month boys and girls spend playing video games. The results are shown in the bar graph below:
a) How many girls played video games for 6-10 hours?
[1 mark]
b) How many boys played video games for less than 16 hours?
[1 mark]
c) What percentage of the girls played video games for 10 hours or less?
[2 marks]
d) To the nearest hour, what was the mean time spent playing video games per week for the boys?
[2 marks]
a) For this question, we need to locate the bar that corresponds to girls and 6-10 hours and take a reading from the top of the bar. Doing so we find 12 girls played video games for 6-10 hours.
b) We need to be careful with this question as It is asking for less than 16 hours, so this means we need to consider all the data to the left of the 16-20 hours bar. The number of boys who played video games for 11-15 hours was 8 and the number of boys who played 6-10 hours was 2.
Therefore the number of boys who played for less than 16 hours was 8+2=10\text{ boys}.
c) For this question, we are looking for 10 hours or less for the girls. This means that we need to look at the first two bars. The number of girls who played for 6-10 hours was 12 and the number who played for 0-5 hours was 8. Therefore the number of girls who played video games for 10 hours or less was 12+8=20\text{ girls}.
This means that 20 out of the total number of girls played for 10 hours or less. However, we don’t know how many girls there were in total, so we will need to add up the totals for each bar. Doing so we find that in total there are 8+12+20+14+8+10+6+2=80\text{ girls}.
Thus 20 out of the 80 girls play video games for 10 hours or less, which works as 25%.
d) To answer this question, we need to work out how many boys there are in each category, the total time spent playing video games for all the boys, and how many boys there are in total.
The total number of boys is 2+8+12+10+18+16+14=80\text{ boys}
If 2 boys played for 9 hours, then this represents 18 hours of playing time.
If 8 boys played for 10 hours, then this represents 80 hours of playing time.
If 12 boys played for 11 hours, then this represents 132 hours of playing time.
If 10 boys played for 12 hours, then this represents 120 hours of playing time.
If 18 boys played for 13 hours, then this represents 234 hours of playing time.
If 16 boys played for 14 hours, then this represents 224 hours of playing time.
If 14 boys played for 15 hours, then this represents 210 hours of playing time.
Therefore the total number of hours of playing time for the boys combined is 18+80+132+120+234+224+210=1018\text{ hours}.
If there are 80 boys who play for a combined total of 1018 hours, then the mean number of hours can be calculated as follows:
\dfrac{1018\text{ hours}}{80\text{ boys}} = 13 \text{ hours}
Question 5: Draw a dual-bar chart on the axes below, for the data below:

[3 marks]
For the vertical y-axis, we will be plotting the frequency (the number of boys / girls). The only thing we need to consider is the scale. Since the lowest value is 0 and the highest value is 9, the y-axis needs to start at 0 and needs to finish at 9 (although the axis can extend slightly beyond 9 if you like).
It is probably the x-axis that is going to cause more problems. Since this is a dual bar chart, the boys and girls columns need to be side by side, but there needs to be a gap between each category. In other words, the bars for boys-that-walk and girls-that-walk touch each other, but the walking and biking categories do not touch since they are completely separate categories.
The widths of the bars should all be the same, as should the gaps between the categories.
Your end result should be similar to the one below:
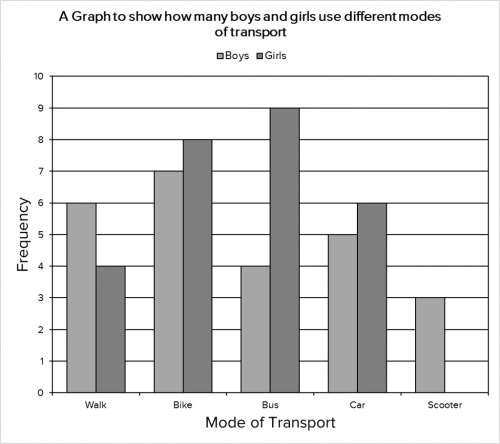
Question 6: A survey is done about the favourite film genres of children and adults attending a cinema on a particular day. The data collected is presented on the composite bar chart shown below.
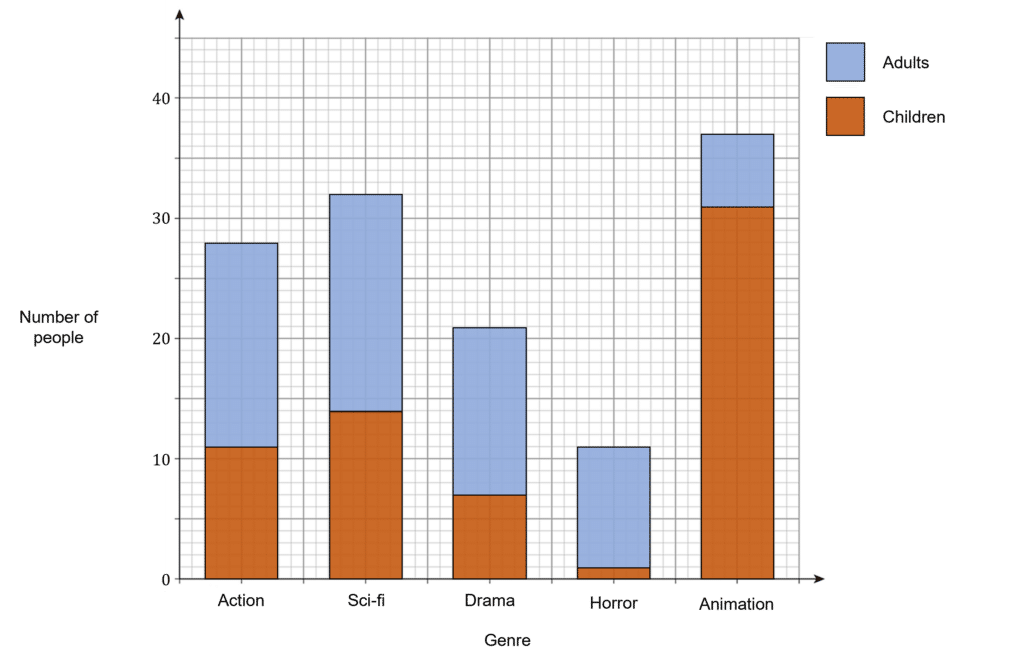
What percentage of adults prefer the drama genre?
Give your answer to one decimal place.
[3 marks]
From the bar chart we can see that 21 people prefer the drama genre.
Number of adults who prefer drama =21-7=14
Total number of adults =(28-11)+(32-14)+(21-7)+(11-1)+(37-31)=65
Percentage of adults who prefer drama =\dfrac{14}{65}\times 100=21.5\% (to one decimal place)
Bar Graphs Worksheet and Example Questions
(NEW) Bar Graphs Exam Style Questions - MME
Level 1-3GCSENewOfficial MME
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now





