Quadratic, Cubic and Harder Sequences
Quadratic, Cubic and Harder Sequences Revision
Quadratic, Cubic and Harder Sequences
Following on from linear sequences, which have a common difference between each term, the sequences found on this page are a bit more complicated, as you have recognise the difference between the differences.
For quadratic and cubic sequences you will need to work out the second and third difference respectively.
Simple Quadratic and Cubic Sequences
For certain simpler quadratic and cubic sequences we can find the nth term by comparing to the list of square and cubic numbers.
Example:
Find the \textcolor{#10a6f3}{n}th term for the quadratic sequence with the following first 5 terms:
\textcolor{#10a6f3}{3,6,11,18,27}
We can see that the differences between each term are not equal.
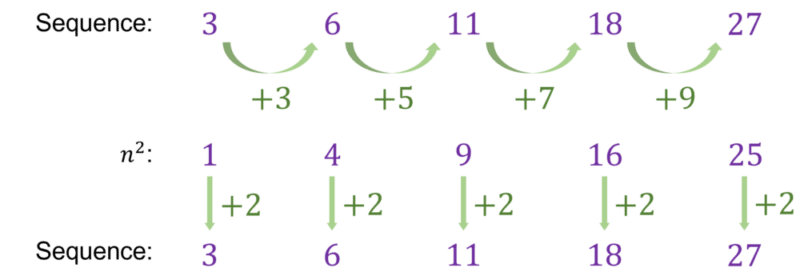
Comparing with the sequence \textcolor{#10a6f3}{n^2}, each term in our sequence is \textcolor{#10a6f3}{2} greater than the corresponding terms in the sequence n^2.
Therefore, we can conclude that the nth term of this sequence is \textcolor{#10a6f3}{n^2+2}.
Quadratic Sequences
For harder quadratic sequences you will be required to work out the second difference (or differences between the differences) to work out the coefficient of the n^2 term in the nth term.
You can then subtract the sequence \textcolor{#00bfa8}{a}n^2 (where \textcolor{#00bfa8}{a} is to be found) term by term away from your original sequence, leaving you with a linear sequence to work with.
Example:
Find the nth term of the sequence with the following first 5 terms
6,8,14,24,38
Firstly we need to find the differences until they are constant.
In this case we can see that the first differences are +2,+6,+10,+14 and then the second difference is \textcolor{#10a6f3}{+4}.
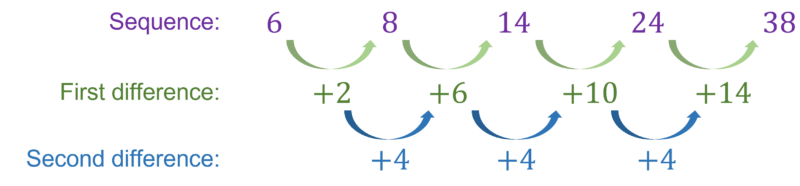
The coefficient of the n^2 term of a quadratic sequence is half of the second difference, which in this case is 4\div2=\textcolor{#00bfa8}{2}.
We then subtract the sequence with nth term 2n^2 away from our original sequence, u_n.

This leaves us with a linear sequence, which has a term to term difference of -4 and therefore an nth term of \textcolor{#10a6f3}{-4n+8}.
Thus the nth term to the quadratic sequence is \textcolor{#10a6f3}{2n^2-4n+8}.
Cubic Sequences
To find the nth term of a cubic sequence we will need to find the first, second and third differences.
Similar to a quadratic sequence you then subtract an^3 from your original sequence, leaving you with a quadratic sequence, where you then follow the same steps as above to find the nth term.
Example:
Find the nth term of the sequence with the following 5 terms
1,28,101,238,457
We need to first find the differences until they are constant.
In this case we can see that the first differences are \textcolor{#10a6f3}{+27,+73,+137,+219}, the second differences are \textcolor{#10a6f3}{+46,+64,+82} and then the third difference is \textcolor{#10a6f3}{+18}.
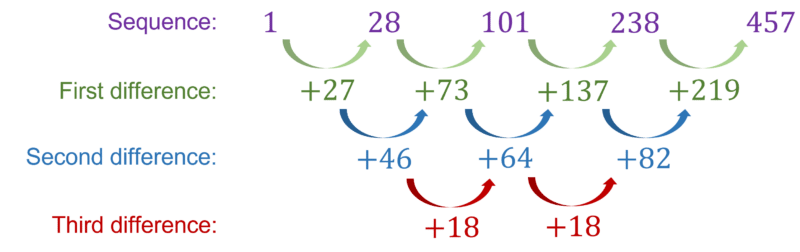
The coefficient of the n^3 term is \textcolor{#00bfa8}{\dfrac{k}{6}}, where \textcolor{#00bfa8}{k} is the constant third difference.
Subtracting 3n^3 away from the sequence:

We are now left with a quadratic sequence with a second constant difference of +10.
So the coefficient of n^2 is 10\div 2=\textcolor{#00bfa8}{5}.
Subtracting 5n^2 away from u_n-3n^3.

This now leaves with us a linear sequence with an nth term of \textcolor{#10a6f3}{-9n+2}.
Hence the nth term of this cubic sequence is \textcolor{#10a6f3}{3n^3+5n^2-9n+2}.
Exponential Sequences
Exponential sequences increase by a common ratio from term to term, with the nth term being defined as
\textcolor{#d11149}{a}\times \textcolor{#00d865}{r}^{(n-1)}where \textcolor{#d11149}{a} is the first term and \textcolor{#00d865}{r} is the value that you multiply by each time.
Example:
An exponential sequence x_n has the first 5 terms
5,15,45,135,405
Find the nth term of the sequence.
To find \textcolor{#00d865}{r}, divide the next term by the previous term.
\textcolor{#00d865}{r}=\dfrac{x_{n+1}}{x_n}=\dfrac{15}{5}=\textcolor{#00d865}{3}
Therefore the nth term is \textcolor{#d11149}{5}\times \textcolor{#00d865}{3}^{(n-1)}, as \textcolor{#d11149}{a=5}.
Quadratic, Cubic and Harder Sequences Example Questions
Question 1: A quadratic sequence has the following first 5 terms
-2,1,6,13,22
Find the nth term of the sequence and hence the 25th term.
[3 marks]
Comparing with the sequence n^2, we can see that each term is 3 less.
So the nth term is n^2-3.
Substituting in n=25 to find the 25th term:
25^2-3=622Question 2: Find the nth term of the quadratic sequence with the following first 5 terms
9,25,47,75,109
[4 marks]
The first differences between terms are +16,+22,+28,+34
The second difference between terms is +6
Therefore, the coefficient of the n^2 term is 6\div 2=3
Subtracting 3n^2 away from the sequence term by term gives us the following linear sequence
6,13, 20,27,34
The nth term of this sequence is 7n-1
Thus, the nth term of the quadratic sequence is 3n^2+7n-1
Question 3: Find the next term of the cubic sequence with the following first 5 terms
4,9,28,73,156
[2 marks]
To work out the next term in this sequence we need to find the first, second and third differences.
First differences: +5,+19,+45,+83
Second differences: +14,+26,+38
Third difference: +12
Working backwards we know that the next second difference will be +50 and therefore the next first difference will be +133.
Therefore, the next term in this sequence is 156+133=289
Question 4: Find the nth term of the cubic sequence with the following first 5 terms
1,6,17,40,81
[5 marks]
First differences: +5,+11,+23,+41
Second differences: +6, +12,+18
Third difference: +6
Coefficient of the n^3 term =6\div6=1
Subtracting n^3 away from the sequence leaves us with the following sequence
0,-2,-10,-24,-44
The first differences of this quadratic sequence are -2,-8,-14,-20 and the second difference is -6
Therefore, the n^2 coefficient is -6\div 2=-3
Subtracting -3n^2 away from the quadratic sequence gives us the linear sequence
3, 10,17,24,31
The nth term of this linear sequence is 7n-4
Putting everything together gives us the nth term of our cubic sequence, which is n^3-3n^2+7n-4
Question 5: An exponential sequence has the following first 4 terms
3,12,48,192
a) Find the nth term of this sequence
[2 marks]
b) Hence or otherwise, find the 10th term of this sequence.
[1 mark]
a) Work out the common ratio, r from term to term.
r=\dfrac{12}{3}=4
Therefore the nth term is 3\times 4^{(n-1)}
b) Substituting n=10 gives
3\times 4^{(10-1)}=786432You May Also Like...

MME Learning Portal
Online exams, practice questions and revision videos for every GCSE level 9-1 topic! No fees, no trial period, just totally free access to the UK’s best GCSE maths revision platform.
