Congruent Shapes
Congruent Shapes Revision
Congruent Shapes
If two shapes are exactly the same – that is, they are the same size, they have the same side lengths, and the same angles – then we say they are congruent.
For most shapes it’s as simple as seeing if they are the same, but for triangles there are 4 rules you need to learn.
Make sure you are happy with the following topics before continuing:
– 2D Shapes and Quadrilaterals
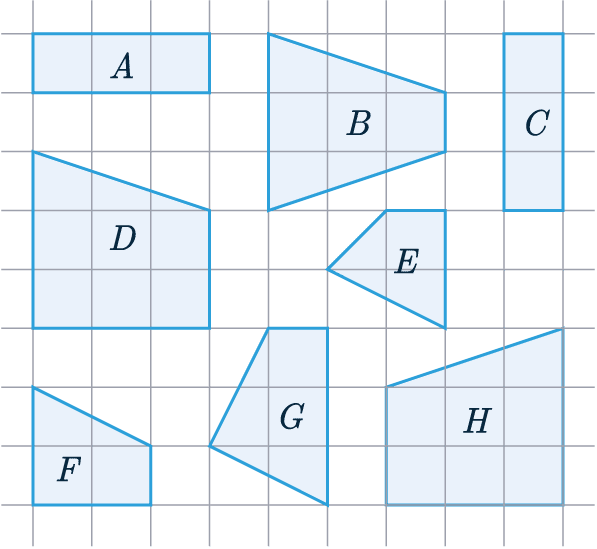
Simple Congruence
For most shapes saying something is congruent is as simple as determining if they are the same size and shape.
Example: Identify two pairs of congruent shapes from the options below.

Shape A – if we were to rotate it by 90\degree then it would fit perfectly onto shape C, so they must be congruent.
Shape A = Shape C
Shape D – we can see that if we take the mirror image of it (which is the same thing as flipping over a paper cut-out), then the result will fit perfectly on top of shape H.
Shape D = Shape H
Take Note: Congruence in Triangles
There is one shape that has its own special rules for congruence and that is the triangle. If we have two triangles which pass one of the 4 rules listed below, then they must be congruent.
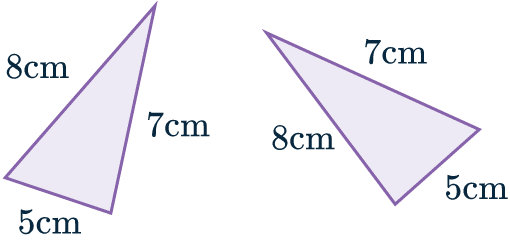
SSS: Side, Side, Side
If two triangles have all three sides in common then they are congruent.

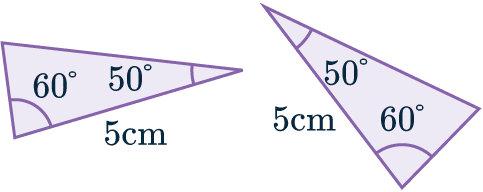
ASA: Angle, Side, Angle

When two triangles have two angles that are the same, and the side length between them is also the same, they are congruent.

SAS: Side, Angle, Side

Two triangles with two sides the same and an angle in between them the same are congruent.

RHS: Right-angle, hypotenuse, side

Two triangles with a right-angle, the hypotenuse, and the adjacent length the same will be congruent.
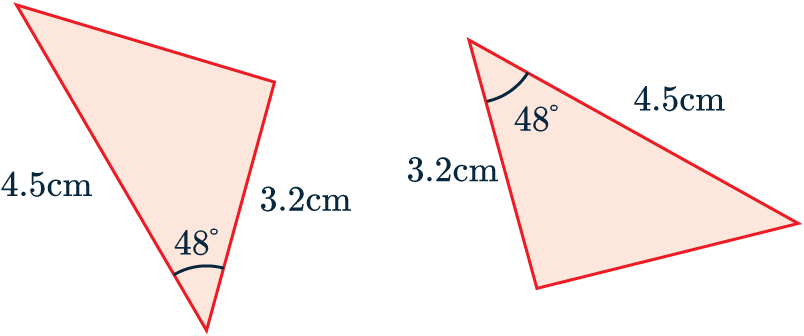
Example 1: Congruent Triangles
State which test you can use to prove that these two triangles are congruent.

We can see that both these triangles have one side that is 3.2cm long, another which is 4.5cm long, and the angle between those two sides is 48\degree in both triangles.
In other words, this pair of triangles passes the SAS test for congruence.
Example 2: Congruent Triangles
Determine which triangle(s) out of B, C, and D is/are congruent to A.
State which test(s) for congruence you used.
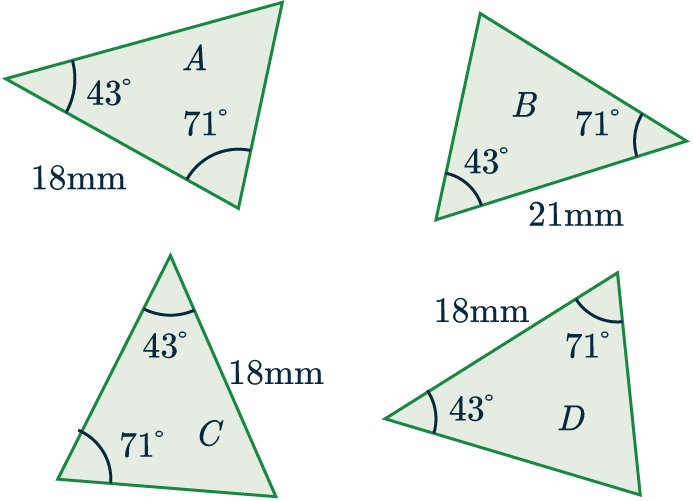
Let’s check each shape individually.
Shape B: has two angles in common with A, but the side is a different length.
Shape C: this has two angles and a side-length in common with A, but to pass the ASA test the side-length needs to be between the two angles, which is not the case for C.
Shape D: this does what shape C didn’t – all the numbers match, and the side we know is between the two angles which means that shape D is congruent to A by the ASA criteria.
Shape D is congruent to shape A.
Congruent Shapes Example Questions
Question 1: Identify 2 pairs of congruent shapes from the options below.
[2 marks]
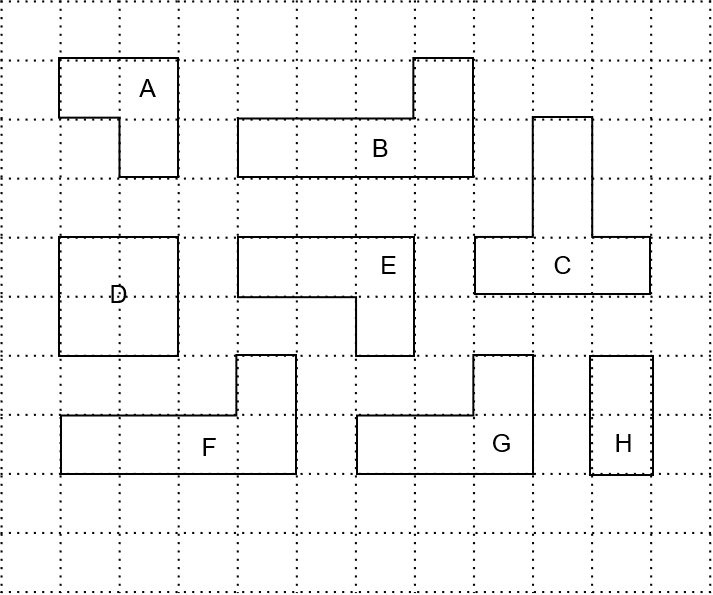
If we were to take shape B and move it downwards and to the left it would fit perfectly on top of shape F, without any need for rotation or flipping. Shapes B and F make the first congruent pair.
If you were to move shape E slightly to the right, you would see that it is the exact mirror image of shape G. In other words, if we were to cut out E and flip it over, the result would fit perfectly onto shape G. Shapes E and G make the second congruent pair.
Question 2: Identify 2 pairs of congruent shapes from the options below.
[2 marks]
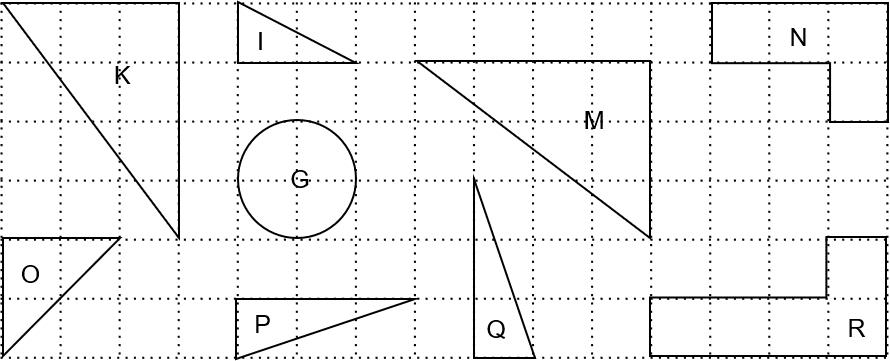
If we were to take shape P, move it across to the right it and rotate it 90 degrees anticlockwise it would fit perfectly on top of shape Q. Hence shapes P and Q make the first congruent pair.
If you were to move shape M slightly to the left and rotate it 90 degrees, you would see that it is the exact mirror image of shape K. In other words, if we were to cut out M and flip it over, the result would fit perfectly onto shape K. Shapes M and K make the second congruent pair.
Question 3: Identify two pair of congruent shapes from the options below.
[2 marks]
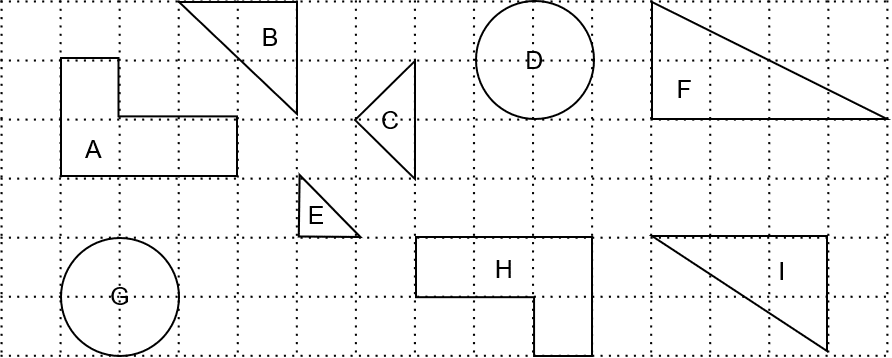
If we were to take shape H, move it across to the left it and rotate it 180 degrees it would fit perfectly on top of shape A. Hence shapes H and A are the congruent.
Also, since D and G are circles of diameter 2, they are congruent.
Question 4: Determine which of the following four triangles are congruent.
State which test for congruence you used.
[3 marks]
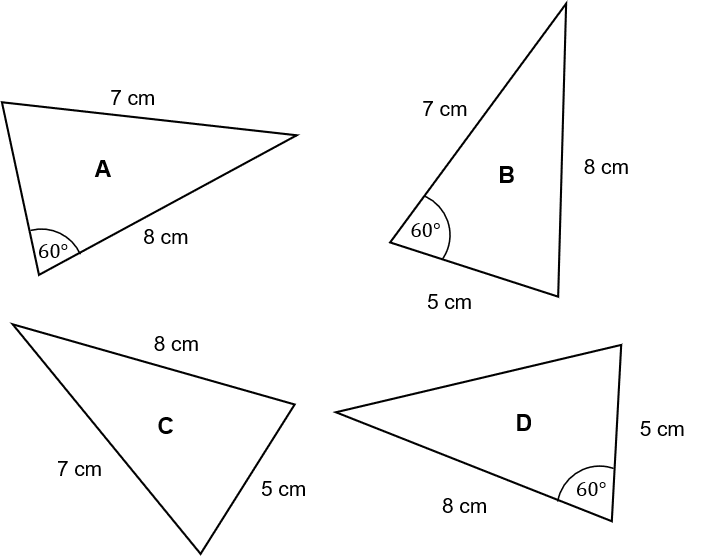
The first thing we should notice is that triangle B actually has more information than we need to test for congruence – all 4 tests require 3 bits of information, but this one has 4. Given this wealth of information, let’s see if anything is congruent to B.
Triangle A: this does have an angle and two sides in common which suggests SAS congruence, but the angle is not between the two known side-lengths, so it is not congruent.
Triangle C: this has 3 side-lengths in common with B, so it must be congruent using the SSS criteria. It doesn’t matter that there’s an extra known angle in A.
Triangle D: this time, we have an angle and two sides in common with B and the angle is in the right place, so it is congruent to B by the SAS criteria.
So, we know that C and D are both congruent to B, or in other words, B, C, and D are all congruent to each other. Given that we determined A was not congruent to B and B has the information of C and D combined, then A must not be congruent to anything, so it remains just B, C, and D.
Question 5: The diagram shows two triangles ABC and XYZ.
Given that sides AB=XZ and CB=XY as well as the angles\angle CBA=\angle ZXY.
Prove that the two triangles are congruent.
[2 marks]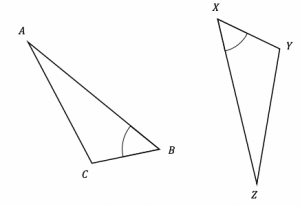
The two triangles can be shown to be congruent by the SAS rule: Two triangles with two sides the same and an angle in between are congruent.
Here the side-angle-side shown are AB-∠CBA-CB and XZ-∠ZXY-XY respectively. Hence triangle ABC and XYZ are congruent.
Congruent Shapes Worksheet and Example Questions
(NEW) Congruent Shapes Exam Style Questions - MME
Level 4-5GCSENewOfficial MME
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now




