Expanding Brackets
Expanding Brackets Revision
Expanding Brackets
Expanding brackets is a key algebra skill that will be require to confidently tackle all sorts of algebra questions.
Make sure you are happy with the following topics before continuing:
Expanding Single Brackets
The process by which we remove brackets is called expanding (or multiplying out) the brackets. This is the opposite process to factorising.
To expand 3(x+2) we need to multiply 3 by x and by 2
\textcolor{red}{3}(\textcolor{limegreen}{x}+\textcolor{blue}{2}) = (\textcolor{red}{3}\times \textcolor{limegreen}{x}) + (\textcolor{red}{3}\times \textcolor{blue}{2}) = \textcolor{red}{3}\textcolor{limegreen}{x} + \textcolor{purple}{6}
This can become harder as the terms get more tricky.
Expanding Double Brackets – Foil Method
When expanding double brackets, we need to multiply each of the things in the first bracket by each of the things in the second bracket. The FOIL method is a way of ensuring this every time.
F – First , O – Outside, I – Inner , L – Last
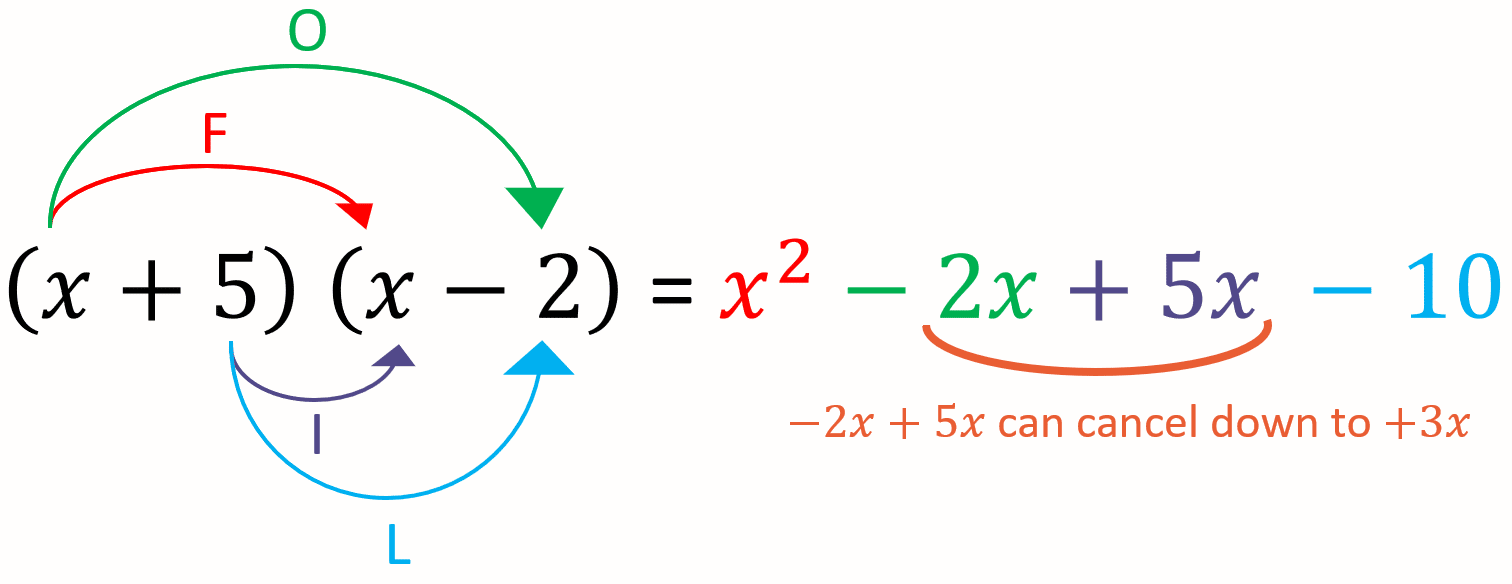
Using the FOIL method will always give your answer in the same form, all you need to do is simplify by collecting the like terms.
\textcolor{red}{x^2} \textcolor{limegreen}{-2x}\textcolor{purple}{+5x}\textcolor{blue}{-10} = \textcolor{red}{x^2} \textcolor{orange}{+ 3x} \textcolor{blue}{-10}

Example 1: Single Brackets
Expand the following, 2(3a+5)
[1 mark]
The green arrow shows the first calculation 2 \times 3a = 6a
The red arrow shows the second calculation 2 \times 5 = 10
This gives the final answer as 6a+10

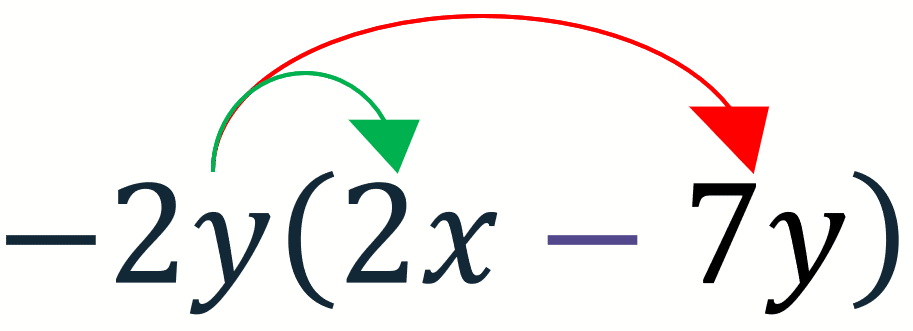
Example 2: Single Brackets
Expand the following, -2y(2x-7y)
[2 marks]
The green arrow shows the first calculation -2y \times 2x = -4xy
The red arrow shows the second calculation -2y \times -7y = 14y^2
This gives the final answer as -4xy+14y^2
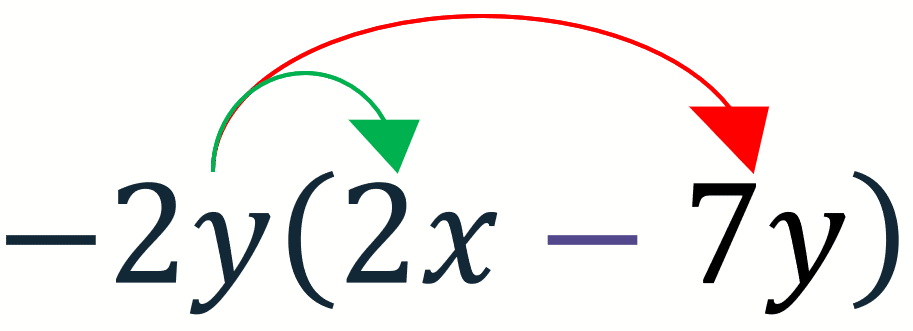
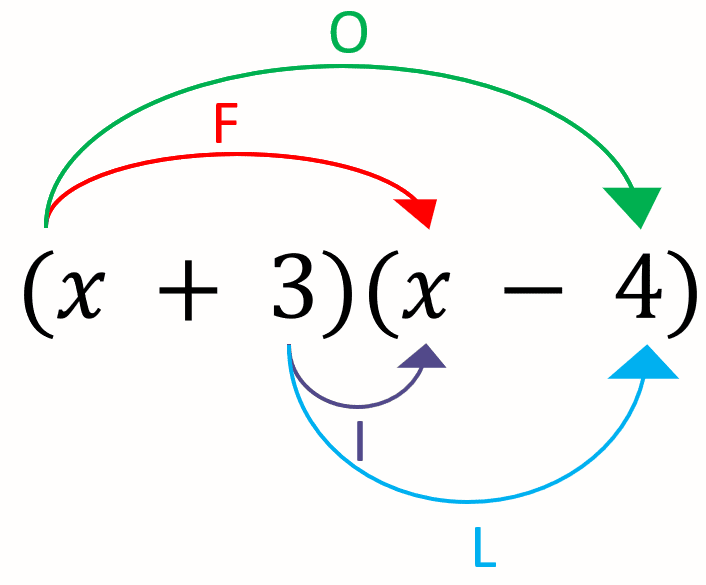
Example 3: Expanding Double Brackets
Using FOIL expand and simplify the following (x + 3)(x - 4).
[3 marks]
Using the FOIL method we get
F = \textcolor{red}{x \times x = x^2}
O = \textcolor{limegreen}{x \times -4 = -4x}
I = \textcolor{purple}{3 \times x = 3x}
L = \textcolor{blue}{3 \times -4 = -12}

We must collect like terms to simplify our answer
\textcolor{red}{x^2} \textcolor{limegreen}{- 4x} \textcolor{purple}{+3x} \textcolor{blue}{-12} = \textcolor{red}{x^2}\textcolor{maroon}{ - x} \textcolor{blue}{- 12}.
Expanding Brackets Example Questions
Question 1: Expand 3xy(x^2 +2x-8)
[2 marks]
We need to multiply everything inside the bracket by 3xy, thus
3xy(x^2 +2x-8) \\ = 3xy \times x^2 + 3xy \times 2x + 3xy \times (-8) \\ = 3x^3y + 6x^2y - 24xy
Question 2: Expand 9pq\left(2 - pq^2 - 7p^4\right)
[2 marks]
We need to multiply everything inside the bracket by 9pq, thus
9pq(2 - pq^2 - 7p^4) \\ =9pq \times 2 - 9pq \times pq^2 - 9pq \times 7p^4 \\ = 18pq -9p^{2}q^3 - 63p^{5}q
Question 3: Expand and simplify (y-3)(y-10)
[3 marks]
We need to make sure that we multiply everything in the left bracket by everything in the right bracket.
By using FOIL or another method of remembering to do every multiplication, we get
(y-3)(y-10) \\ = y\times y+y\times(-10)+(-3)\times y +(-3)\times(-10) \\ =y^2 -10y -3y +30
Then, collecting like terms we get the result of the expansion to be
y^2 -13y + 30
Question 4: Expand and simplify (m + 2n)(m - n)
[3 marks]
We need to make sure that we multiply everything in the left bracket by everything in the right bracket.
By using FOIL or some other method of remembering to do every multiplication, we get
(m+2n)(m-n) \\ = m\times m+m\times(-n)+2n\times m +2n\times(-n) \\ = m^2 -nm +2nm - 2n^2
Then, collecting like terms we get the result of the expansion to be
m^2 + nm - 2n^2
Question 5: Expand and simplify (2y^2+3x)^2
[3 marks]
First, we can write this as two sets of brackets,
(2y^2+3x)^2=(2y^2+3x)(2y^2+3x)
By using FOIL and collecting like terms, we get
(2y^2+3x)(2y^2+3x) \\ =2y^2\times2y^2+2y^2\times3x+3x\times2y^2+3x\times3x \\ =4y^4+6xy^2+6xy^2+9x^2 \\ = 4y^4+12xy^2+9x^2
Expanding Brackets Worksheet and Example Questions
(NEW) Expanding Single Brackets Exam Style Questions - MME
Level 4-5GCSENewOfficial MME(NEW) Expanding Double Brackets Exam Style Questions - MME
Level 4-5GCSEExpanding Brackets Drill Questions
Algebra Expand And Factorise
Level 4-5GCSEAlgebra Quadratics Expand and Factorise
Level 4-5GCSEMultiplying Out Brackets
Level 4-5GCSE
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now





