Expanding Triple Brackets
Expanding Triple Brackets Revision
Expanding Triple Brackets
Expanding triple brackets is just an extension of expanding single and double brackets. Fortunately, this new kind of expansion isn’t really a new kind at all. The ideas are much the same as when we expanded double brackets, it’s just the messier algebra that makes it tricky.
Make sure you are happy with the following topics before continuing:
Expanding Triple Brackets
When expanding triple brackets, we just multiply the first two brackets together, then multiply the result with the final bracket.
Example: Expand the following, \textcolor{red}{(x+1)}\textcolor{limegreen}{(x+2)}\textcolor{blue}{(3x+3)}
Step 1 – Multiply out the first two brackets (use FOIL)
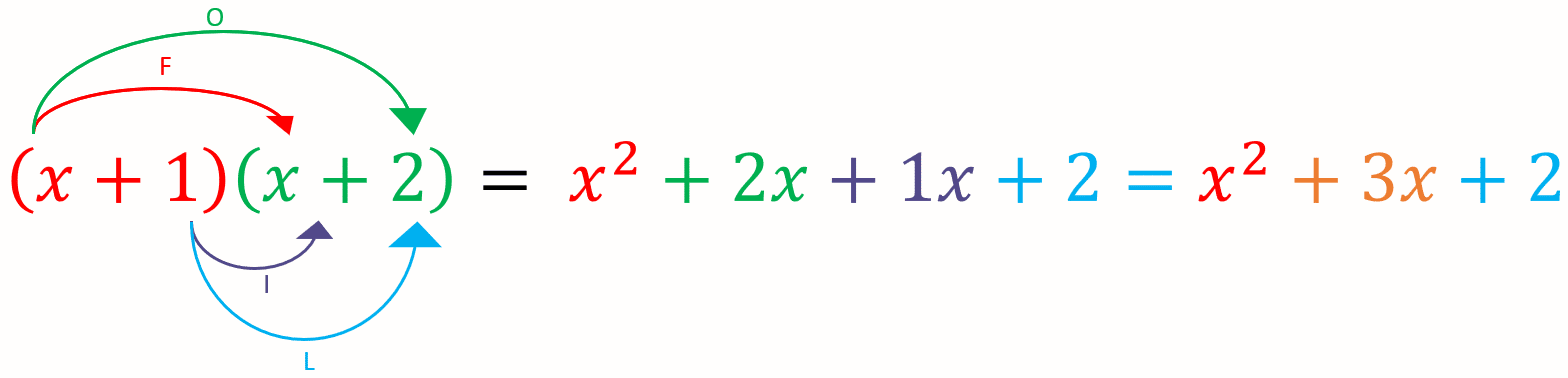
Step 2 – Multiply the result x^2 +3x+2 by (3x+3)
This requires \bf{6} separate multiplications, shown below.
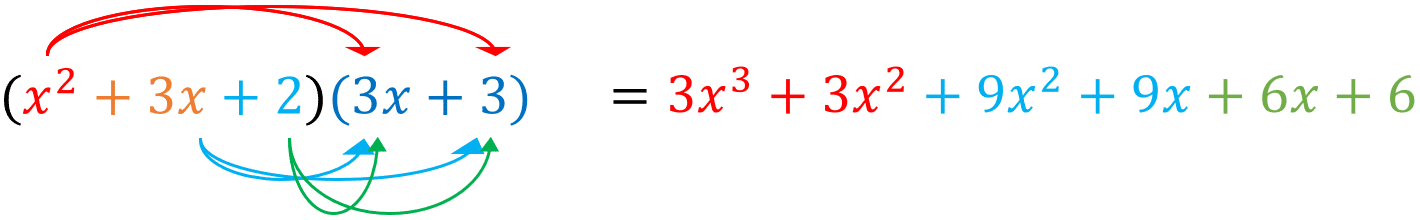
Finally we must collect the like terms
\textcolor{red}{3x^3+3x^2}\textcolor{blue}{+9x^2+9x}\textcolor{limegreen}{+6x+6} = 3x^3 + 12x^2 +15x + 6
Example 1: Expanding Triple Brackets
Expand and simplify the following, \textcolor{red}{(x + 1)}\textcolor{limegreen}{(x+3)}\textcolor{blue}{(x - 2)}.
[4 marks]
Step 1 – Multiply out the first two brackets (use FOIL)
\begin{aligned} \textcolor{red}{(x+1)}\textcolor{limegreen}{(x+3)} &=\textcolor{red}{x^2}\textcolor{limegreen}{+3x}\textcolor{purple}{+x}\textcolor{blue}{+3} \\ &=\textcolor{red}{x^2}\textcolor{maroon}{+4x}\textcolor{blue}{+3}\end{aligned}
Step 2 – Next we must multiply the result (\textcolor{red}{x^2}\textcolor{maroon}{+4x}\textcolor{blue}{+3}) by \textcolor{blue}{(x - 2)}
(\textcolor{red}{x^2}\textcolor{maroon}{+4x}\textcolor{blue}{+3})\textcolor{blue}{(x - 2)} = x^3 + 4x^2 +3x -2x^2 -8x-6 \\ = x^3+2x^2-5x-6
Example 2: Expanding Triple Brackets
Expand and simplify the following, \textcolor{red}{(a+5)}\textcolor{limegreen}{(2a-1)}\textcolor{blue}{(3+a)}.
[4 marks]
Step one – Multiply out the first two brackets (use FOIL)
\begin{aligned}\textcolor{red}{(a+5)}\textcolor{limegreen}{(2a-1)} & =\textcolor{red}{2a^2}\textcolor{limegreen}{-a}\textcolor{purple}{+10a}\textcolor{blue}{-5} \\ &=\textcolor{red}{2a^2}\textcolor{maroon}{+9a}\textcolor{blue}{-5}\end{aligned}
Step 2 – Multiply the result (\textcolor{red}{2a^2}\textcolor{maroon}{+9a}\textcolor{blue}{-5}) by \textcolor{blue}{(3+a)}
(\textcolor{red}{2a^2}\textcolor{maroon}{+9a}\textcolor{blue}{-5})\textcolor{blue}{(3 + a)} = 6a^2 + 2a^3 +27a +9a^2 -15 -5a \\ = 2a^3 +15a^2 +22a -15
Expanding Triple Brackets Example Questions
Question 1: Expand and simplify (m+8)(m-9)(m+1)
[4 marks]
Firstly, we expand the second two brackets into a normal quadratic,
\begin{aligned}(m-9)(m+1)&=m^2+m-9m-9 \\ &=m^2-8m-9\end{aligned}
Then, replacing the second two brackets with their expanded version, we can rewrite the original expression:
(m+8)(m-9)(m+1)=(m+8)(m^2-8m-9)
We will now expand these two brackets, first multiplying the m in the left-hand bracket by everything in the right-hand bracket, and then multiplying the 8 in the left-hand bracket by everything in the right-hand bracket. Doing so, we get
(m+8)(m^2-8m-9)=m^3-8m^2-9m+8m^2-64m-72
Collecting and simplifying like terms, we get the simplified expansion to be,
m^3-73m-72
Question 2: Expand and simplify (2k-3)(k+4)^2
As (k+4)^2 is the same as (k+4)(k+4) the expression can also be written like,
(2k-3)(k+4)(k+4)
This then looks like all the other triple bracket expansions we’ve seen, and we can continue as normal. Firstly, we expand the second two brackets into a normal quadratic,
\begin{aligned}(k+4)(k+4)&=k^2+4k+4k+16 \\ &=k^2+8k+16\end{aligned}
Then, replacing the second two brackets with their expanded version, we can rewrite the original expression:
(2k-3)(k+4)(k+4)=(2k-3)(k^2+8k+16)
We will now expand these two brackets, first multiplying the 2k in the left-hand bracket by everything in the right-hand bracket, and then multiplying the -3 in the left-hand bracket by everything in the right-hand bracket. Doing so, we get,
(2k-3)(k^2+8k+16)=2k^3+16k^2+32k-3k^2-24k-48
Collecting and simplifying like terms, we get the simplified expansion to be,
2k^3+13k^2+8k-48
Question 3: Expand and simplify (x+1)(x+2)(x-4)
[4 marks]
Firstly, we expand the second two brackets into a normal quadratic,
\begin{aligned}(x+2)(x-4)&=x^2+2x-4x-8 \\ &=x^2-2x-8\end{aligned}
Then, replacing the second two brackets with their expanded version, we can rewrite the original expression:
(x+1)(x+2)(x-4)=(x+1)(x^2-2x-8)
We will now expand these two brackets, first multiplying the x in the left-hand bracket by everything in the right-hand bracket, and then multiplying the 1 in the left-hand bracket by everything in the right-hand bracket. Doing so, we get
(x+1)(x^2-2x-8)=x^3-2x^2-8x+x^2-2x-8
Collecting and simplifying like terms, we get the simplified expansion to be,
x^3-x^2-10x-8
Question 4: Expand and simplify (a+b)^3
[4 marks]
We can write the expression given in the question as,
(a+b)^3=(a+b)(a+b)(a+b)
This then looks like all the other triple bracket expansions we’ve seen, and we can continue as normal. Firstly, we expand the second two brackets into a normal quadratic,
\begin{aligned}(a+b)(a+b)&=a^2+ab+ba+b^2 \\ &=a^2+2ab+b^2\end{aligned}
Then, replacing the second two brackets with their expanded version, we can rewrite the original expression:
(a+b)^3=(a+b)(a^2+2ab+b^2)
We will now expand these two brackets, first multiplying the a in the left-hand bracket by everything in the right-hand bracket, and then multiplying the b in the left-hand bracket by everything in the right-hand bracket. Doing so, we get,
(a+b)(a^2+2ab+b^2)=a^3+2a^2b+ab^2+a^2b+2ab^2+b^3
Collecting and simplifying like terms, we get the simplified expansion to be,
a^3+3ab^2+3a^2b+b^3
Question 5: Expand and simplify (x-3)(2x+5)(x+2)
Firstly, we expand the second two brackets into a normal quadratic,
\begin{aligned}(2x+5)(x+2)&=2x^2+4x+5x+10 \\ &=2x^2+9x+10\end{aligned}
Then, replacing the second two brackets with their expanded version, we can rewrite the original expression:
(x-3)(2x+5)(x+2)=(x-3)(2x^2+9x+10)
We will now expand these two brackets, first multiplying the x in the left-hand bracket by everything in the right-hand bracket, and then multiplying the -3 in the left-hand bracket by everything in the right-hand bracket. Doing so, we get,
(x-3)(2x^2+9x+10)=2x^3 +9x^2+10x-6x^2-27x-30
Collecting and simplifying like terms, we get the simplified expansion to be,
2x^3+3x^2-17x-30






