Fractions Decimals and Percentages
Fractions Decimals and Percentages Revision
Fractions, Decimals, and Percentages
Fractions, decimals and percentages are just different ways of expressing a proportion of a value. Each is equally valid and the choice of which is used is down to the context and/or setting it is being used in.
Here we will explain how to convert between fractions, decimals, and percentages (in both directions).
Common Conversions
In shops, you will frequently see discounts written as 50\% off or \dfrac{1}{2} price but never as 0.5 times the original cost. Similarly when converting currency, the exchange rate will never be be quoted as a percentage but rather as a decimal.
All three are mathematically equivalent ways of saying the same thing but we default to using the one that is most appropriate in that scenario.
The table shows some important common conversions between fractions, decimals and percentages that you should remember.
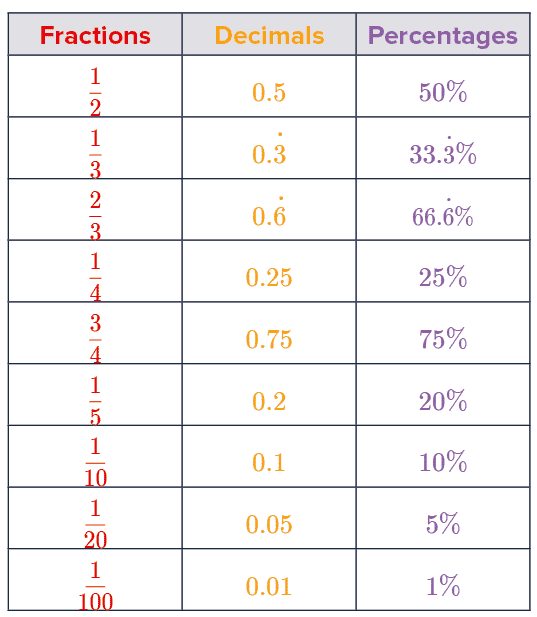
Fractions to Decimals to Percentages
Convert fractions to decimals – treat the fraction like a division and divide the number on the top by the number on the bottom. e.g. \dfrac{9}{20} = 9 \div 20 = 0.45
Convert decimals to percentages – multiply by 100 (move the decimal point right 2 places). e.g. 0.45 \times 100 = 45\%

Percentages to Decimals to Fractions
Convert percentages to decimals – divide by 100 (shift the decimal point left 2 places). e.g. 64 \% \div 100 = 0.64
Convert decimals to fractions – for terminating decimals (i.e. decimals that don’t go on forever) we write the decimal as a fraction with 1 on the bottom. Then, keep multiplying top and bottom by 10 until the decimal becomes a whole number. Then you can simplify the fraction if needed.
e.g. 0.79 = \dfrac{0.79}{1} = \dfrac{7.9}{10} = \dfrac{79}{100}
For recurring decimals it can be more tricky (see the recurring decimals to fractions page)

Example 1: Percent and Decimal Conversions
a) Write 37\% as a decimal.
[1 mark]
To convert this to a decimal we will divide by 100, so we get 37 \div 100 = 0.37
b) Write 0.548 as a percentage.
[1 mark]
To convert this to a percentage we will multiply by 100, so we get 0.548 \times 100 = 54.8\%
Example 2: Fraction to Decimal
a) Write \dfrac{12}{25} as a decimal.
[2 marks]
Dividing 12 by 25 doesn’t sound too pleasant, but there is a way we can change the fraction (before dividing top by bottom) to make life easier. Notice that 25\times 4=100 and dividing by 100 is straightforward. So, if we multiply top and bottom by 4 we get
\dfrac{12}{25} \times \dfrac{4}{4} =\dfrac{48}{100}=0.48
b) Write \dfrac{11}{8} as a decimal.
[2 marks]
In this case, there is no nice shortcut. We’ll just have to divide 11 by 8 in whichever way feels most comfortable – here, we’ll go for the bus stop method.
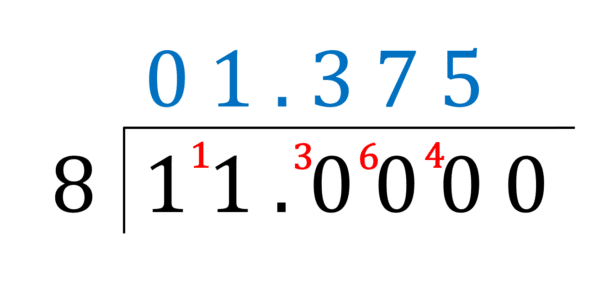
Doing this, we get the picture shown above, (click here to revise the bus stop method) and we see that the result is,
\dfrac{11}{8} = 1.375
Example 3: Decimal to Fraction
Write 4.56 as a fraction in its simplest form.
[2 marks]
Any number divided by 1 is equal to itself, so we can write 4.56 as \dfrac{4.56}{1}.
Now, if we multiply top and bottom by 100 we get
\dfrac{4.56}{1}=\dfrac{4.56\times 100}{1\times 100}=\dfrac{456}{100}
All that remains now is to simplify it. Cancelling down,
\dfrac{456}{100} = \dfrac{228}{50} = \dfrac{114}{25}
Example 4: Percentage to Fraction
Write 48.1\% as a fraction.
[1 mark]
Percentages are already out of 100, so
48.1\%=\dfrac{48.1}{100}
Then, multiplying top and bottom by 10 (to make the numbers whole) we get
48.1\% = \dfrac{481}{1000}
Example 5: Fraction to Percentage
Write \dfrac{4}{5} as a percentage.
[1 mark]
Firstly, let’s convert it to a decimal. Notice that if we times top and bottom by 2, the fraction becomes
\dfrac{4}{5}=\dfrac{4\times 2}{5\times 2} = \dfrac{8}{10} = 8\div 10 = 0.8
Then, to convert this decimal to a percentage, we times by 100:
0.8 \times 100 = 80\%
Note: Alternatively, if you can write a fraction with 100 on the denominator, then the value on the top immediately gives you what the fraction would be as a percentage. For example, \dfrac{34}{50}=\dfrac{68}{100}=68\%
Fractions Decimals and Percentages Example Questions
Question 1: Write 54.4\% as a decimal.
[1 mark]
We can express this percentage as a decimal simply by dividing by 100,
55.4\%\div100=0.544
Question 2: Write 16.4\% as a fraction in its simplest form.
[2 marks]
We can express this percentage as a fraction by dividing by 100,
\dfrac{16.4}{100}
To make the numbers whole, we multiply top and bottom by 10,
\dfrac{16.4\times 10}{100 \times 10}=\dfrac{164}{1,000}
Now, we simplify until there are no common factors left. So, we find,
\dfrac{164}{1,000}=\dfrac{82}{500}=\dfrac{41}{250}
Question 3: Write \dfrac{17}{40} as a decimal.
[2 marks]
We will treat the fraction like a division and divide 17 by 40,
\;\;\;\;\;0\;0.\;\;4\;\;\;2\;\;\;5\\40\overline{\left)1{}^17.{}^{17}0{}^{10}0{}^{20}0\right.}
Therefore,
\dfrac{17}{40}=0.425
Question 4: Write 0.256 as a fraction in its simplest form.
[2 marks]
We can express this decimal as a fraction,
0.256=\dfrac{0.256}{1}
To make the numbers whole, we multiply top and bottom by 1000,
\dfrac{0.256}{1}\times \dfrac{1000}{1000}=\dfrac{256}{1000}
Now, we simplify until there are no common factors left. So, we find,
\dfrac{256}{1000}=\dfrac{32}{125}
Question 5: Write \dfrac{13}{20} as a decimal.
[1 mark]
A simpler method than diving 13 by 20 in its current form is to notice that 20 \times 5 = 100 and dividing by 100 is straightforward. So, if we multiply top and bottom by 5 we get,
\dfrac{13}{20}\times\dfrac{5}{5}=\dfrac{65}{100} = 0.65
Fractions Decimals and Percentages Worksheet and Example Questions
(NEW) Fractions to Decimals to Percentages Exam Style Questions - MME
Level 1-3GCSE
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now





