Invariant Points
Invariant Points Revision
Invariant points
When we transform a shape – using translations, reflections, rotations, enlargements, or some combination of those 4, there are sometimes points on the shape that end up in the same place that they started. These are known as invariant points.
You are expected to identify invariant points.
Make sure you are happy with the following topics before continuing:
Example 1: Invariant Points – Reflections
Shape A is shown below.
State the coordinates of any invariant points when shape A is reflected in the line x=1.
[1 mark]
In order to see if there are any invariant points in a transformation, we need to do the transformation.
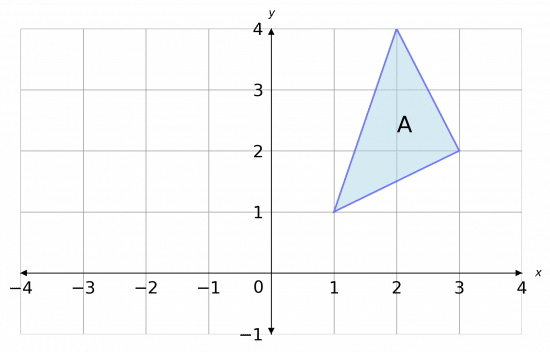
First, we draw the line x=1. It is a horizontal line that passes through 1 on the x-axis.
Then, completing the reflection we get the picture shown below.
The reflected shape is shown in green.
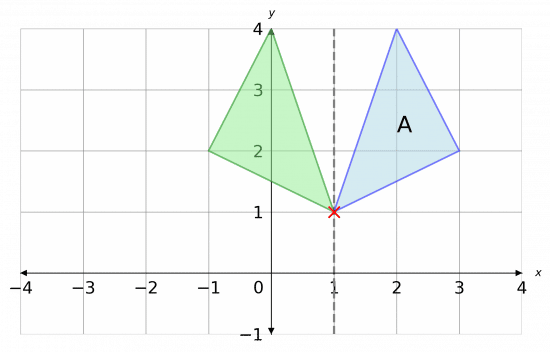
As we can see, all points on the shape have moved to a different location except for one the one that was located on the reflection line.
Here we’ve marked this with a red X.
So, we can conclude that there is 1 invariant point, and the coordinates of it are
(1, 1)
Example 2: Invariant Points – Translation
Perform the following two transformations to shape A, in the given order:
- Rotate 180\degree about the point (1, 0)
- Translate by the vector \begin{pmatrix} 2 \\ 2 \end{pmatrix}.
Label the final shape C and state the coordinates of any invariant points.
[2 marks]
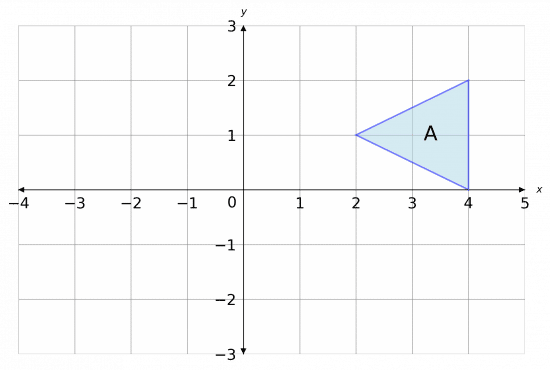
Firstly, we need to perform the rotation. Here, we’ll mark a point at (1, 0) to note the centre of rotation, and then we’ll call the resulting shape B.
Then, we have to translate by the vector
\begin{pmatrix} 2 \\ 2 \end{pmatrix}
This means moving shape B 2 to the right, and then 2 up.
This completes the transformation, so we label the resulting shape C. The full picture is shown below.
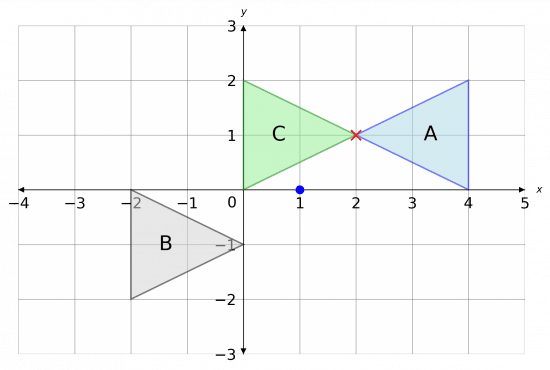
We can now see one invariant point between C and A, with coordinates
(2, 1)
Here, marked with a red X.
Invariant Points Example Questions
Question 1:
a) Enlarge shape A by scale factor 2 about the origin.
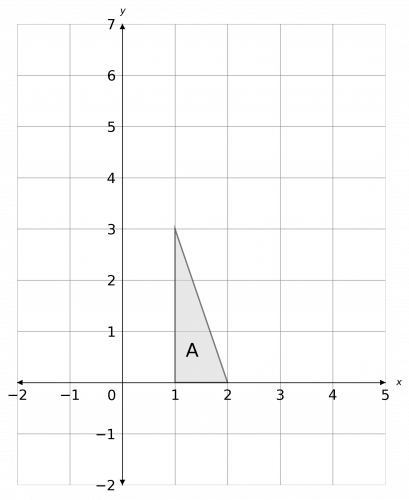
b) State the number of invariant points.
[3 marks]
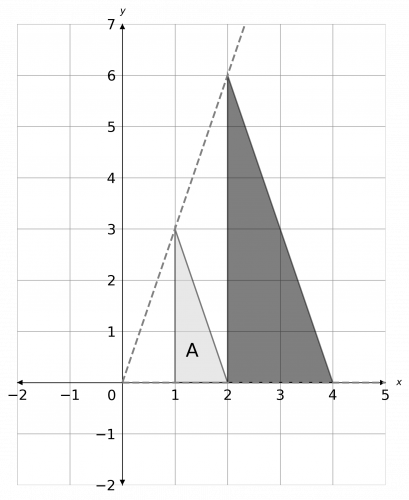 a) To do the enlargement, we draw lines for the origin through each of the corners of the shape, extending them twice as far to account for the scale factor 2. Then, joining the corners together, we get the enlarged shape as shown below.
a) To do the enlargement, we draw lines for the origin through each of the corners of the shape, extending them twice as far to account for the scale factor 2. Then, joining the corners together, we get the enlarged shape as shown below.
b) Looking at the graph, we can see that none of the points on the triangle ended up being in their original spot. Therefore, the number of invariant points is zero.
Question 2:
a) Perform the following two transformations to shape A in this order:
• Reflect in the line x=0.
• Rotate by 180\degree about the point (0, 1).
Label the transformed shape B.
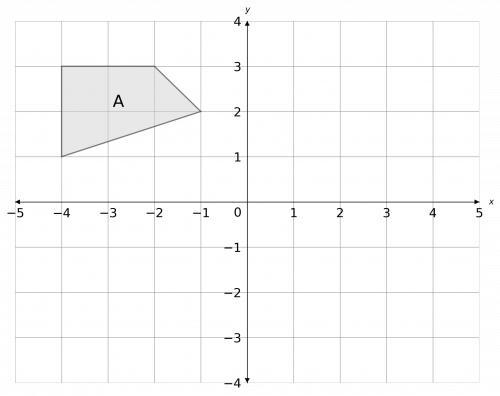
b) Write down the coordinates of the invariant point.
[3 marks]
A reflection in the line x=0 is just a reflection in the y-axis. The result of this is shown in grey below.
Then, taking this new shape and rotating it 180\degree about (0, 1) (using tracing paper or otherwise), we get the shape labelled B below.
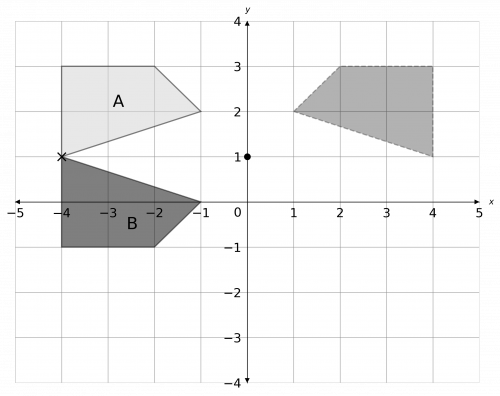
b) Looking at the graph, we can see there is one corner of the shape that ends up in its original position. Reading off, we see that the coordinates of the invariant point are
(-4, 1)
Question 3:
a) Reflect shape A in the line y=x. Label the new shape B.
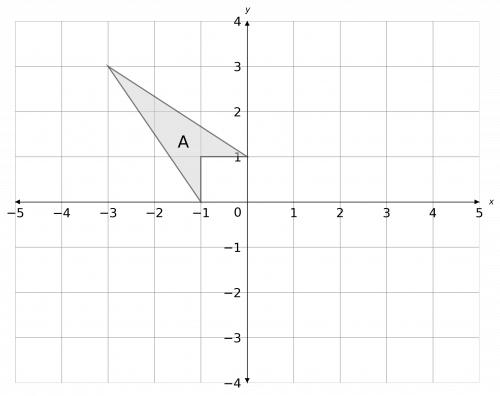
b) Describe the translation that, when done to shape B, will result in exactly two invariant points between the new shape and shape A.
[3 marks]
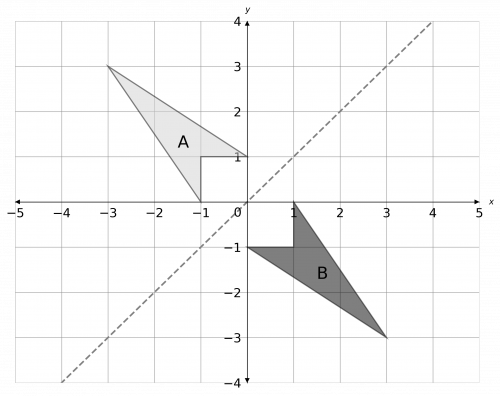
a) The line y=x is the straight line that passes through the origin, and points such as (1, 1), (2, 2), and so on. Reflecting the shape in this line and labelling it B, we get the picture below.
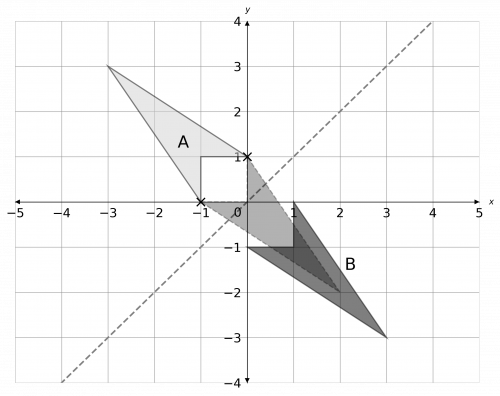
b) We want to perform a translate to B to make it have two point that are invariant (with respect to shape A). To do this, we want the two sharp corners at the bottom of the arrow shapes to meet. This can be done by moving shape B left by 1 and up by 1, as shown below.
Therefore, the required transformation to get two invariant points is a translation by the vector
\begin{pmatrix} -1 \\ 1 \end{pmatrix}
Invariant Points Worksheet and Example Questions
(NEW) Invariant points Exam Style Questions - MME
Level 6-7NewOfficial MME
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now





