Perimeter
Perimeter Revision
Perimeter
The perimeter of a 2D shape is the distance around the edges of the shape. It is found by adding up the lengths of each individual edge of the shape. This can be easy for simple shapes and harder for composite shapes.
Make sure you are happy with the following the following topics:
Perimeter of Simple Shapes
The rectangle shown below has a length of 11cm and a width of 3cm.
Calculate the perimeter of the rectangle shown.

The opposite sides of a rectangle are equal in length.
So, the two sides that are not labelled must also be 3 cm and 11 cm.
Therefore, we get
Perimeter = 3+3+11+11=28 cm
Perimeter of Compound Shapes
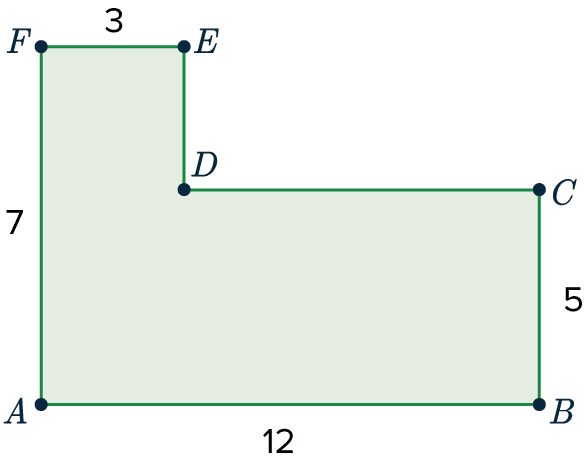
ABCDEF is a composite shape made up of rectangles.
Calculate the perimeter of shape ABCDEF.

Usually, with compound shapes there will be some missing sides which need to be calculated.
First we need to calculate ED.
We can see that FA = ED + CB, so we can calculate:
7 = 5 + ED
ED = 2
Next, we do the same with DC.
AB = FE + DC
12 = 3+DC
DC = 9
Finally, we can calculate the perimeter by adding up all the side lengths.
3 + 2+ 9 + 5+ 12+ 7 = 38
Example 1: Compound Shapes
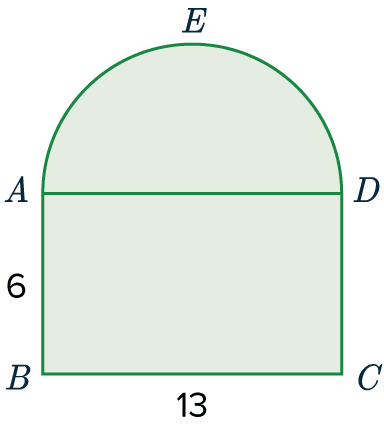
ABCDE is a shape made up of a rectangle and a semi-circle.
AB = 6,\,BC=13.
Calculate the perimeter of this shape to 3 significant figures.
[2 marks]

With compound shapes we first need to break it up into two parts.
1) Rectangle – We know that rectangles have two pairs of equal sides, so we know that DC=6 and AD=13. However, since it is not on the outside of the shape, we won’t be counting AD with the perimeter. Therefore, the perimeter so far (sides AB, BC, and CD) is
6+13+6=25
2) Semi-circle – The formula for the circumference of a circle is \pi d, where d is the diameter. Because it is a semi-circle we’re dealing with, we will half the result. Doing this, we get
AED=\dfrac{(\pi \times 13)}{2}=20.420...
Now, adding the values together we get the total perimeter to be
25+20.420...=45.4 (3 sf)
Example 2: Perimeter of Triangles
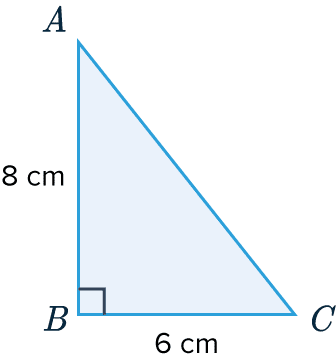
ABC is a triangle. AB = 8 cm, BC = 6 cm. Angle ABC is a right-angle. Calculate the perimeter of triangle ABC.
[2 marks]
In this case, we are given two sides of the triangle but will have to work out the third if we want to find the perimeter. Since this is a right-angled triangle, we can use Pythagoras! Pythagoras’ theorem says
a^2+b^2=c^2,
Where c is the hypotenuse and a and b are the other two sides. So, the equation becomes
8^2+6^2=AC^2
Evaluating the left-hand side, and then square rooting, we get
AC^2=64+36=100
AC=\sqrt{100}=10\text{ cm}
Now we have all three sides, simply add them to get the perimeter:
6+8+10=24\text{ cm}

Perimeter Example Questions
Question 1: ABCD is square with an area of 64\text{m}^2.
Calculate the perimeter of ABCD.
[2 marks]

To find the perimeter, we need to find the length of one side (all sides are the same, since it’s a square). If we say that x is the length of one side, then the area is,
x^2=64
So, if we square root both sides, we find that x=8. Therefore, the perimeter of the square is,
8+8+8+8=32\text{ m}
Question 2: ABCDEF is a regular hexagon. Its perimeter is 21 cm.
Calculate the length of one side.
[2 marks]
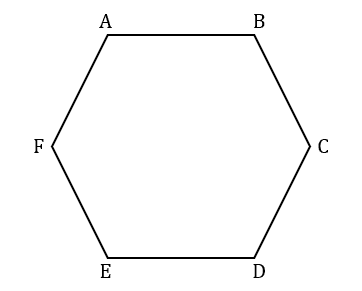
This hexagon is regular, so all 6 of its sides must be the same length. Since the perimeter is the result of adding all the sides together, we get:
\text{Length of one side}=21 \div 6=3.5\text{ cm}
Question 3: The semi-circle below has centre O and a radius of 5 cm.
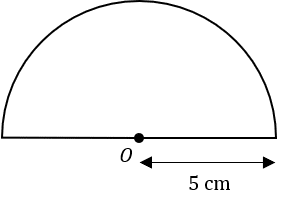
Find the perimeter of the semi-circle. Give your answer to 1 decimal place.
[2 marks]
Perimeter of semi-circle arc can be calculated by finding half of the circumference of a complete circle:
\dfrac{1}{2}\times\pi\times10=5\pi cm
Length of base = 10 cm
Total Perimeter = 10 +5\pi = 25.7 cm
Question 4: The diagram below shows a rectangle with a section missing.
Work out the perimeter of the shape.
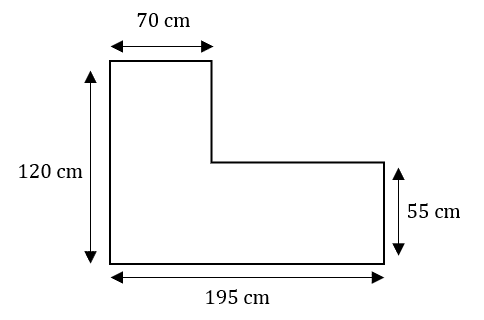
[3 marks]
To find the perimeter, we first need to find the missing lengths:
120-55=65 cm
195-70=125 cm
Hence adding all the lengths together:
Total Perimeter =120+70+65+125+55+195=630 cm
Question 5: ABC is an isosceles triangle. The perimeter of ABC is 45 cm.
Work out the value of x.
[3 marks]
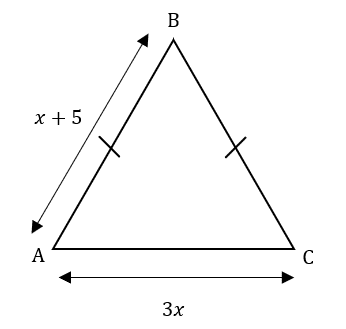
Here we are given the perimeter, whilst the side-lengths are expressed in terms of x. Since this triangle is an isosceles triangle, we know that,
AB = BC = x+5
Adding together the three sides:
(x+5) + (x+5) + 3x= 45 \text{cm}
Now, to find x we must solve this equation,
\begin{aligned}5x+10&=45 \\ 5x&=35 \\ x&= 35\div5=7\text{cm}\end{aligned}
Perimeter Worksheet and Example Questions
(NEW) Perimeter Exam Style Questions - MME
Level 4-5GCSENewOfficial MME
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now





