Pie Charts
Pie Charts Revision
Pie Charts
A pie chart is a circular chart used to compare the sizes of data sets in relation to one another.
Make sure you are happy with the following topics before continuing.
How to Draw a Pie Chart
Start by drawing a circle with a compass, and then measure the angles with a protractor to make sure we get them right.
To measure the size of each slice, we use the size of the angle that it will take up, out of the total 360\degree of the circle. To calculate the angle, we use the following formula:
\textcolor{black}{\text{angle }}=\dfrac{\textcolor{black}{\text{number of things in that category}}}{\textcolor{black}{\text{total number of things}}}\times \textcolor{black}{360\degree}
Note: Knowing how to use a compass and protractor will come in handy for other topics and will save time in the exam so make sure you get plenty of practise.
Example 1: Drawing a Pie Chart
Brian asks 60 people what their favourite colour is and separates the answers into 5 categories. His results are shown in the table below. Draw a pie chart to display Brian’s results.
[4 marks]

To draw the pie chart, we need to calculate the size of the angle needed for each category using the formula.
\text{‘Red’ angle }=\dfrac{10}{60}\times 360=60\degree
\text{‘Blue’ angle }=\dfrac{13}{60}\times 360=78\degree
\text{‘Green’ angle }=\dfrac{24}{60}\times 360=144\degree
\text{‘Yellow’ angle }=\dfrac{5}{60}\times 360=30\degree
\text{‘Other’ angle }=\dfrac{8}{60}\times 360=48\degree
Now we have all the angles, we can draw the chart.
Example 2: Interpreting Pie Charts
A survey was done asking 90 people how many bathrooms were in their home. Freddie drew a pie chart to display the results of this survey.
a) What number of bathrooms was most common in this survey?
[1 mark]
b) Calculate the number of people who have 1 bathroom in their house.
[2 marks]
c) If Freddie picks someone at random from the group surveyed, what is the probability that he chooses a person with exactly 1 bathroom in their home?
[2 marks]
a) Clearly, ‘2 bathrooms’ has the biggest slice, so the most common number of bathrooms is 2.
b) To work out how many people had exactly 1 bathroom in their house, we will have to use a protractor to measure the size of the angle in the ‘1 bathroom’ slice.
We can see that the angle for this sector is 100\degree. Using the pie chart formula,
\textcolor{black}{\text{number of things in category}}= \textcolor{black}{\dfrac{\text{angle}}{360\degree}} \times \textcolor{black}{\text{total number of things}}
Subbing in the numbers we get,
Number of people with 1 bathroom =\dfrac{100}{360}\times 90=25
c) To find the probability of randomly picking someone with 1 bathroom, we just find the proportion of people with 1 bathroom as a fraction of the total. Doing this, we get
probability of picking someone with 1 bathroom =\dfrac{100}{360}=\dfrac{5}{18}
Pie Charts Example Questions
Question 1: The pie chart shows the colours of the jumpers that 32 students wore to school for a non-uniform day. How many students wore a red jumper?
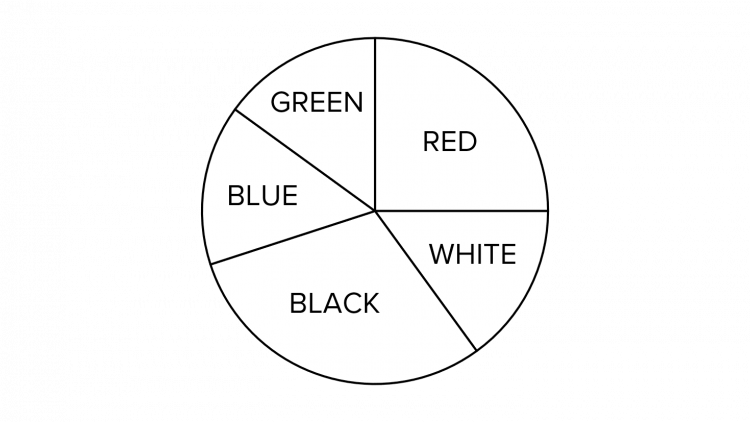
[2 marks]
From the pie chart, we can see that the slice representing red jumpers is a right angle which tells us that this slice is exactly one quarter of the circle.
Therefore, one quarter of the class wore a red jumper on this non-uniform day:
32\text{ students}\div4 = 8\text{ students}
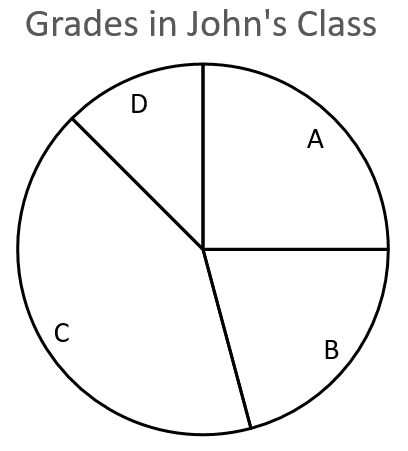
Question 2: John recorded the grades his class received on a piece of homework in the table shown below:

Draw a pie chart to represent John’s data.
[3 marks]
We have to work out the size of the angle that each grade ‘slice’ should have. We know that John recorded the grades of 24 pieces of homework (6+5+10+3=24).If 6 of the 24 pieces of homework were awarded a grade A, we can write this as a fraction :\dfrac{6}{24} or \dfrac{1}{4}.
Therefore \frac{1}{4} of the pie will be the slice for grade A so one quarter of the whole pie chart will be a slice with a right-angle (90\degree) since,
360\degree \div 4 = 90\degree
Homework that was awarded a grade B can be expressed as the following fraction:\dfrac{5}{24}. Since we know that there are 360\degree in a circle, then the angle for the grade B slice must be \frac{5}{24} of 360\degree:
\dfrac{5}{24} \times 360\degree = 75\degree
The angle for the grade C slice must be \frac{10}{24} of 360\degree:
\dfrac{10}{24} \times 360\degree = 150\degree
The angle for the grade D slice must be \frac{3}{24} of 360\degree:
\dfrac{3}{24} \times 360\degree = 45\degree
Drawing the circle with a compass, and measuring the angles with a protractor, we should have a pie chart like the one shown below:
Question 3: The below pie chart shows the colours of cars that passed underneath a bridge during a one-hour period. A total of 510 cars passed beneath the bridge. The number of yellow cars is represented by an angle of 60 degrees. How many yellow cars passed under the bridge?
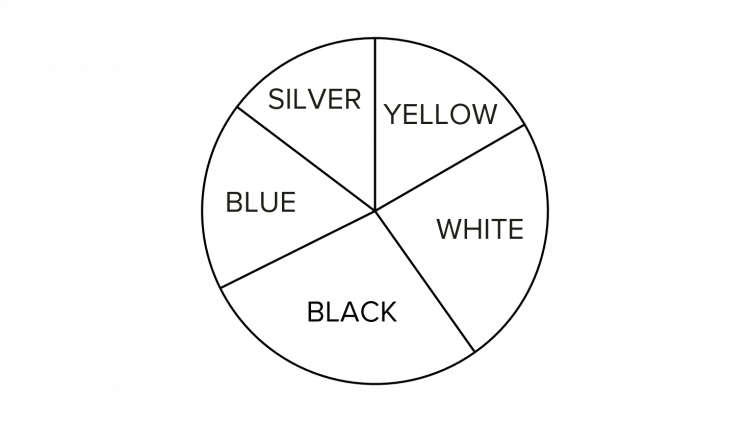
[2 marks]
We know that 510 cars passed underneath the bridge and that the number of yellow cars is represented by a slice of 60 degrees.
We know that in a circle there is a total of 360\degree, thus the proportion of yellow cars can be expressed as the following fraction:
\dfrac{60\degree}{360\degree}
If \frac{60}{360} of the total number of cars were yellow, then the number of yellow cars can be calculated as follows:
\dfrac{60}{360}\times 510\text{ cars} = 85\text{ yellow cars}
Question 4: The pie chart shows different makes of cars in an airport car park.
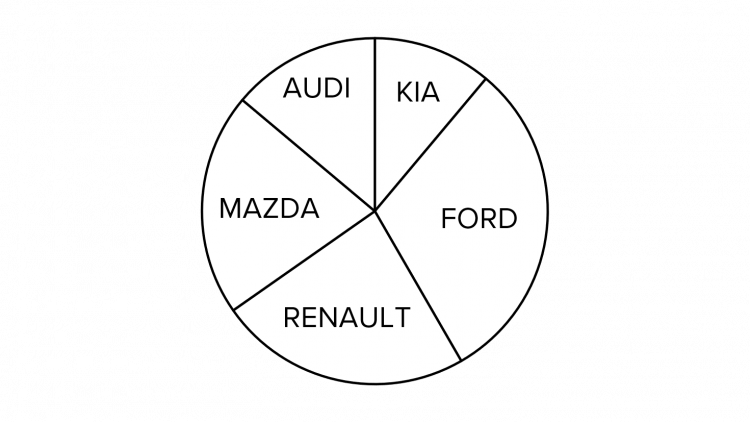
There are 600 Kia cars, which is represented by an angle of 40\degree.
a) How many Renault cars are there if they are represented by an angle of 85\degree?
[2 marks]
b) How many cars are there in total in the airport car park?
[2 marks]
Question 4: The pie chart shows different makes of cars in an airport car park.

There are 600 Kia cars, which is represented by an angle of 40\degree.
a) How many Renault cars are there if they are represented by an angle of 85\degree?
[2 marks]
b) How many cars are there in total in the airport car park?
[2 marks]
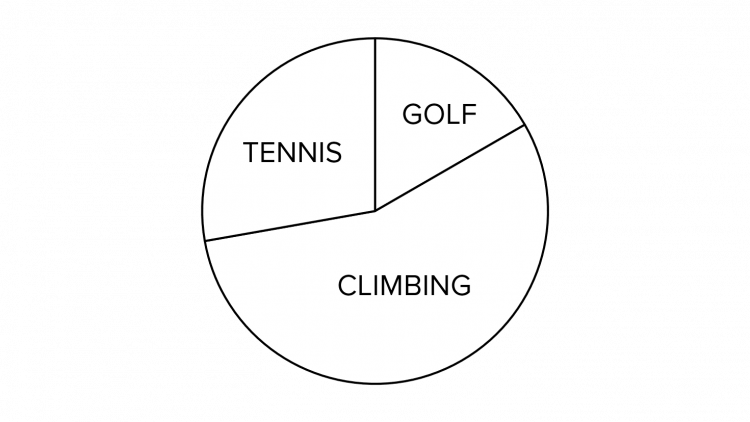
Question 5: Oliver and Lewis spend their leisure time by pursuing various sports such as golf, tennis and climbing. Oliver has 12 hours of leisure time per week, the breakdown of this time is shown in the pie chart below, where the angle of the slice representing golf is 60 degrees.
Lewis has 9 hours of leisure time per week, and the breakdown of his leisure pursuits is shown in the below pie chart:
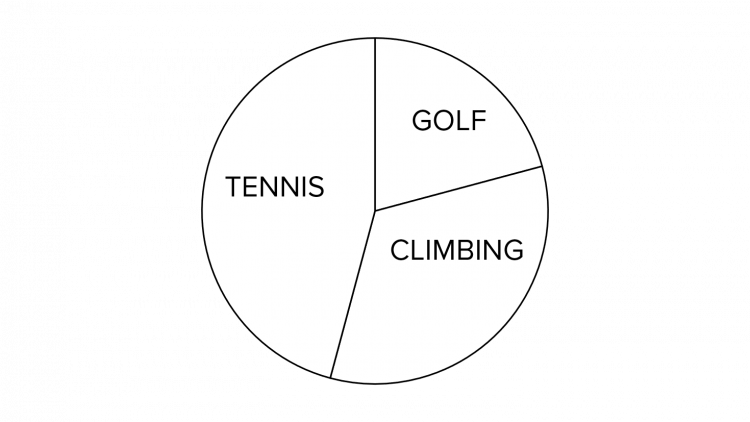
If Lewis spends the same amount of time as Oliver each week playing golf, then how many degrees should the slice representing golf be?
[3 marks]
The first thing we need to work out in this question is the amount of time that Oliver spends playing golf.
We are told that he has 12 hours of leisure time in total and that this is represented by a 60\degree slice of the pie chart. Since we know that there are 360\degree in a circle, then the proportion of the time that Oliver spends playing golf can be expressed as follows:
\dfrac{60\degree}{360\degree}
We can therefore calculate the amount of time he playing golf as follows:
\dfrac{60}{360}\times12\text{ hours} = 2 \text{ hours}
If Lewis spends 2 hours of the available 9 playing golf, this will be represented by \frac{2}{9} of the pie chart. Since the pie chart is a full circle (360\degree), then the slice of the pie chart can be calculated as follows:
\dfrac{2}{9} \times 360\degree = 80\degree
Pie Charts Worksheet and Example Questions
(NEW) Pie Charts Exam Style Questions - MME
Level 4-5GCSENewOfficial MME
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now