Prime Numbers
Prime Numbers Revision
Prime Numbers
A prime number is a special type of number that can only be divided by 1 and itself; they only appear in their own times table.
Skill 1: Factors and Multiples
A multiple of a number is just a number that appears in its times table.
A factor is a number by which another number can be divided. A pair of factors can be multiplied together to give the original number.
For example, if we want to list the factors of the number 12, we need to find the numbers that 12 can be divided by. We can write them out as pairs:
1 \times 12 = 12
2 \times 6 = 12
3 \times 4 = 12
We can say that 1, 2, 3, 4, 6 and 12 are all factors of 12. Another way of saying this is that 12 is a multiple of each of its factors.
Skill 2: Understanding Prime Numbers
Another way of describing prime numbers is that they are numbers with only two positive factors. There are some important facts you should know about prime numbers:
- The number \textcolor{black}1 is not a prime number – it has only one positive factor (itself!)
- The number \textcolor{red}2 is the only even prime number
- Except for \textcolor{red}2 and \textcolor{red}5, all prime numbers end in \textcolor{red}1, \textcolor{red}3, \textcolor{red}7 or \textcolor{red}9
- Not all numbers ending in \textcolor{black}1, \textcolor{black}3, \textcolor{black}7 and \textcolor{black}9 are prime
- There is no pattern in the series of prime numbers
The prime numbers between \textcolor{black}1 and \textcolor{black}{50} are displayed below.

Skill 3: Finding Prime Numbers
You may be asked to show whether or not a number is prime. There are a couple of things to bear in mind that make this process a lot easier:
- Ignore any numbers that end in \textcolor{blue}0, \textcolor{blue}2, \textcolor{blue}4, \textcolor{blue}6 and \textcolor{blue}8 – these are even numbers and are all divisible by \textcolor{blue}2 (except for 0 itself!)
- If you think a number is prime, and it does not divide exactly by \textcolor{red}3 or \textcolor{red}7 then it is a prime number. This applies to all prime numbers less than 120
- For prime numbers larger than 120, you may have to try dividing them by many other numbers
Skill 4: Prime Factor Trees
Prime numbers are the ‘building blocks’ of other larger numbers. We can divide a number into it’s factors and keep dividing these factors by their factors until we are left with nothing but prime numbers – this is called prime factorisation. We use factor trees to find the prime factorisation of a number.
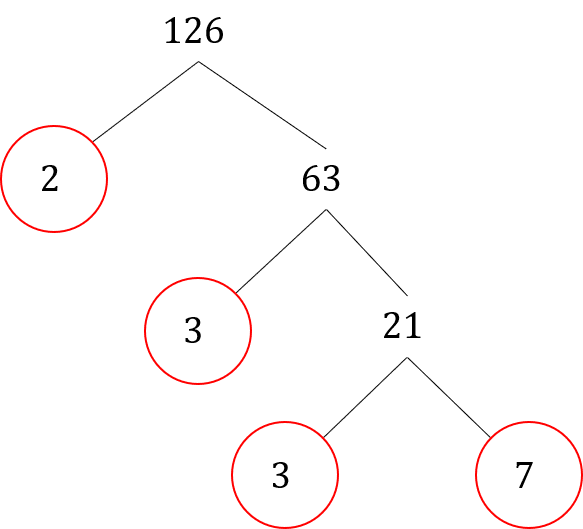

Example: find the prime factorisation of 126
First, recognise that 126 is an even number so it is divisible by 2:
126\div2 = 63
We are left with 2 and 63. \textcolor{red}2 is a prime number, so we circle it.
Next, we can divide 63 by 3:
63 \div 3 = 21
We are left with 3 and 21. \textcolor{red}3 is a prime number, so we circle it.
Next, we can divide 21 by 3:
21\div3=7
We are left with 3 and 7 which are both prime numbers, so we circle them both.
There are no more ways we can divide the factors as we are left with prime numbers only. We can now write the prime factorisation as:
2\times3\times3\times7=126
We can convert this to index form by grouping the numbers that are the same into powers:
2\times3^2 \times7 = 126
Example 1: Finding a Prime Number
Determine whether the following numbers are prime:
25, 31, 57, 84
The number 25 is divisible by 5 so it is not prime: 25 \div 5 = 5
The number 31 cannot be divided by any number other than 1 and itself, so it is prime.
The number 57 is divisible by 3 so it is not prime: 57 \div 3 = 19
The number 84 is divisible by 2 so it is not prime: 84 \div 2 = 42
Prime Numbers Example Questions
Question 1: Show that the number 39 is not a prime number.
[1 mark]
To show that a number is not prime, we just need to find a pair of factors other than 1 \times itself.
Another pair of factors of 39 are:
13\times3=39
Therefore 39 is not a prime number.
Question 2: find all the prime numbers in the following list:
20,21,22,23,24,25,26,27,28,29
[1 mark]
First, cross out all the even numbers:
\cancel{20},21,\cancel{22},23,\cancel{24},25,\cancel{26},27,\cancel{28},29
We are now left with the following numbers:
21,23,25,27,29
We can cross out 25 as all prime numbers end in either 1, 3, 7 or 9.
We are now left with:
21,23,27,29
21\div3 = 7 so 21 is not a prime number.
27\div 3 = 9 so 23 is not a prime number.
23 and 29 have only two factors each;
1\times23 = 23 and 1 \times 29 = 29
Therefore 23 and 29 are the only prime numbers in the list.
Question 3: List the first 5 multiples of 8
[1 mark]
We need to list the first 5 numbers in the 8 times table. These are:
8,16,24,32,40
Question 4: List all the factors of 48
[1 mark]
It is easiest to list factors in pairs:
1\times48 = 48
2\times24 = 48
3\times16=48
4\times12=48
6\times8=48
Therefore the factors of 48 are:
1,2,3,4,6,8,12,16,24,48
Question 5: Give the prime factorisation of 72
[2 marks]
There are many factor pairs of 72, but the easiest way to find the prime factorisation is to start by dividing by 2:

We can carry on dividing the factors by 2 until we are left with an odd number (9), at which point we can divide by 3.
We are left with the prime factorisation:
2\times2\times2\times3\times3 = 2^3 \times 3^2 = 72



