Sequences and Nth Term
Sequences and Nth Term Revision
Sequences
In maths, a sequence is a list of numbers, algebraic terms, shapes, or other mathematical objects that follow a pattern or rule. There are two different ways you will be expected to work out a sequence:
- A term-to-term rule – each term in the sequence is calculated by performing a fixed set of operations (such as “multiply by 2 and add 3”) to the term(s) before it.
- A position-to-term rule – each term in the sequence is calculated according to its position in the sequence. Usually, this takes the form of an n^{th} term formula.
For quadratic sequences, please visit the Quadratic Sequences Revision Page
Finding a Sequence from the n^{th} Term
Some sequences have a rule called an n^{th} term rule, which tells you how to generate terms.
The n^{th} term rule is always an expression in n.
To find the first term in the sequence, substitute n=1 into the expression. To find the second term in the sequence, substitute n=2 into the expression. And so on.
Example: A sequence has the n^{th} term rule 2n+1. Find the first four terms.
First term: n=1
2n+1=2\times1+1=3
Second term: n=2
2n+1=2\times2+1=5
Third term: n=3
2n+1=2\times3+1=7
Fourth term: n=4
2n+1=2\times4+1=9
The first four terms are: 3, 5, 7 and 9.
Finding the n^{th} term for a Linear Sequence
Linear sequences (or arithmetic progressions) are sequences that increase or decrease by the same amount between each term.
Want a way to express any term in a concise mathematical way? This can be done using the n^{th} term formula. This is a rule that gives you the value of any term in the sequence in the form,
an+b,
Where a and b are numbers to be determined.
Example: Find the n^{th} term for the following sequence, 3, \, 7, \,11, \,15, \,19, \, ...

Step 1: Find the Common Difference (a)
The common difference is the amount the sequence increases (or decreases) each time.
a=4, because a is always the difference between each term.
Step 2: Determine if you need to Add or Subtract anything (b)
To work out b, consider the sequence formed by putting n=1, 2, 3, 4, 5 into 4n:
4, 8, 12, 16, 20
What’s the difference between these terms and our actual sequence? They’re all too big by 1. So, to make our original sequence, we must subtract 1 from 4n.
Step 3: Write the formula in the correct form (an+b)
Thus, our n^{th} term formula is
4n-1.
Geometric Sequences
Another type of sequence is a geometric sequence or geometric progression.
In a geometric sequence, you multiply each term by a common ratio to get to the next term. For example,
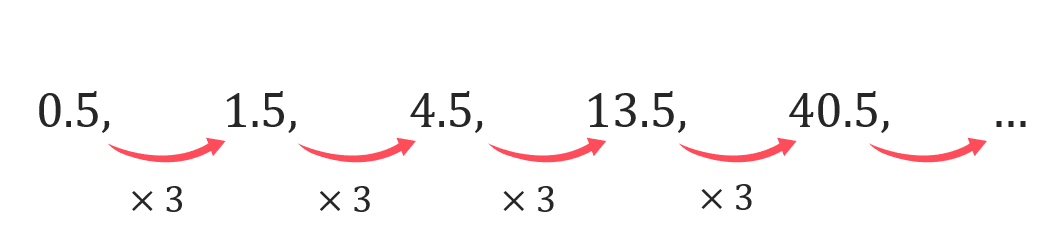
is a geometric progression where to get get to the next term you have to multiply the previous term by the common ratio. Therefore to find the next two terms of this sequence we have to multiply the preceding term by 3, so
40.5\times 3=121.5 and 121.5\times 3 =364.5
Geometric Sequences involving Surds
You may be asked about geometric sequences involving surds. For example,
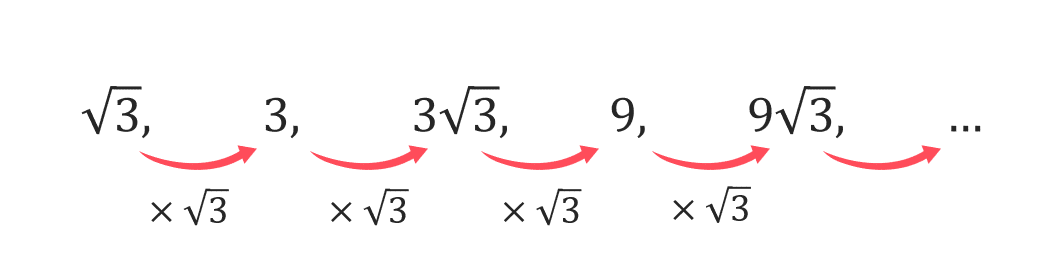
is a geometric progression where the common ratio is not a rational number. The method of finding the next two terms of this sequence is the same as before, multiply the preceding term by \sqrt{3}, so
9\sqrt{3}\times 3=27 and 27\times \sqrt{3} = 27\sqrt{3}
Other Types of Sequences
There are other types of sequences you should be familiar with:
Triangular Numbers
Triangular numbers are numbers that can be represented as an equilateral triangle of dots.
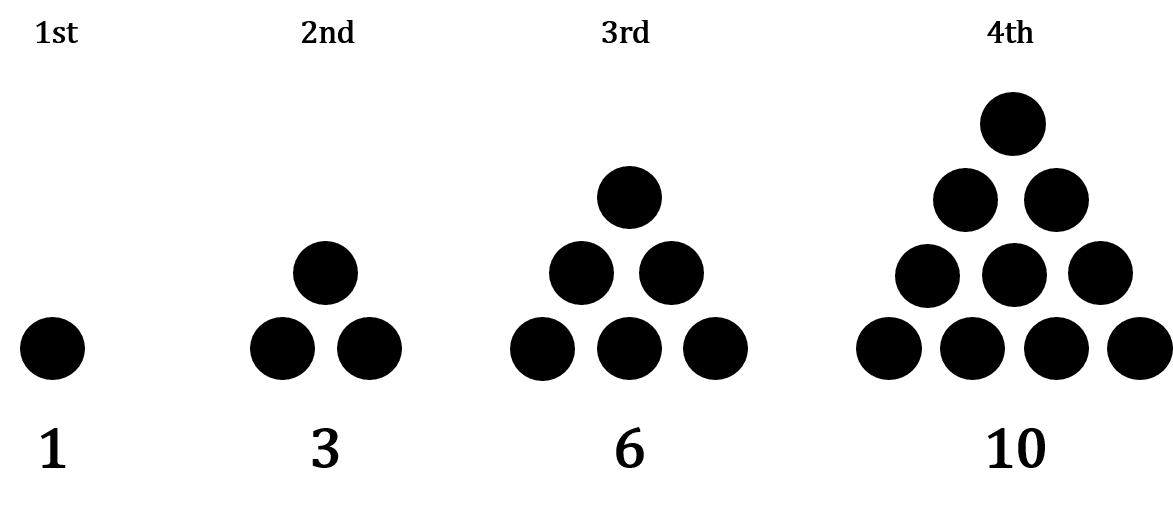
The n^{th} term is \dfrac{n(n+1)}{2}, giving
1, 3, 6, 10, 15, 21, ...
Square Numbers
These sequences are made up of square numbers so the n^{th} term is n^2, giving
1, 4, 9, 16, 25, 36, 49, ...
Cubic Numbers
These sequences are made up of cubic numbers so the n^{th} term is n^3, giving
1, 8, 27, 64, 125, 216, ...
The Fibonacci Numbers
The first few terms of the Fibonacci sequence are:
1, 1, 2, 3, 5, 8, 13, 21, ...
This is a famous sequence that you need to recognise. The rule is the previous 2 terms are added together in the sequence to get the next term.
Note:
Subscript notation can be used to denote position to term and term to term rules.
For example
x_{n+1}=3x_n-4 shows that you multiply the previous term by 3 and subtract 4 to get the next term.
y_n=5n+3 gives you a rule for the nth term of a sequence.
Example 1: Linear Sequences
Find the n^{th} term formula for the sequence -2, 5, 12, 19, 26.
[2 marks]
The first step is to find the common difference between each term.
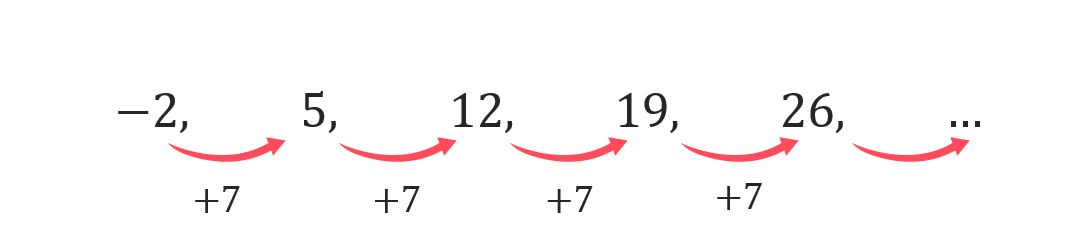
Hence we can write the n^{th} term as,
7n+b
To work out b, consider the sequence formed by putting n=1, 2, 3, 4, 5 into u_n=7n:
7, 14, 21, 28, 35
The difference between these numbers and our sequence is we need to subtract 9 from each term. Thus, our n^{th} term is
7n-9.
Example 2: Determining if a Value is Part of a Sequence
The first five terms of a sequence are:
-3, 1, 5, 9, 13
Determine if 1143 is part of this sequence.
[3 marks]
Step 1: First we must find the n^{th} term of the sequence of the sequence as before, this gives
4n-7.
Step 2: Next we need to write the n^{th} term as an euqation equal to 1143 and solve for n
If n solves to give an integer, then 1143 is part of the sequence.
\begin{aligned} 4n-7&=1143 \\ 4n & = 1150 \\ n&= 287.5\end{aligned}
As 287.5 is not an integer, 1143 must not be part of the sequence.
Example 3: Solving Problems involving Sequences
The sum of two consecutive terms in a sequence given by the n^{th} term, 3n+8 is 109. Find the values of these two terms.
[4 marks]
In this case we have to first set up an equation, setting the first term as n and the second as n+1, such that,
\begin{aligned} 3n+8+3(n+1)+8 & = 109 \\ 3n + 8 + 3n + 3 + 8 & = 109 \\ 6n +19 &= 109 \\ 6n &= 90 \\ n &=15 \end{aligned}
Hence, it is the 15th and 16th terms we are looking for which are,
3(15)+8 = 53 and 3(16) +8 = 56
Sequences and Nth Term Example Questions
Question 1: A sequence has the n^{th} term 4n+1
a) Find the 12^{th} term in this sequence
[1 mark]
b) A term in this sequence is 77. Find the position of this term in the sequence.
[2 marks]
a) To find the 12^{th} term of this sequence, we will substitute n=12 into the formula given.
4(12)+1=49
So, the 12^{th} term is 49
b) Every term in this sequence is generated when an integer value of n is substituted into 4n+1
Hence if we set 77 to equal 4n+1, we can determine its position in the sequence,
4n+1=77
making n the subject by subtracting 1 then dividing by 4,
n=\dfrac{77-1}{4}=19
Hence 77 is the 19^{th} term in the sequence.
Question 2: A sequence is defined by the formula 5n-4
a) Work out the first 5 terms of this sequence.
[2 marks]
b) Explain why 108 is not a term in this sequence.
[2 marks]
a) To generate the first 5 terms of this sequence, we will substitute n=1, 2, 3, 4, 5 into the formula given.
\begin{aligned}1 &=5(1)-4 =1 \\ 2 &=5(2)-4 =6 \\ 3 & =5(3)-4=11 \\ 4 &=5(4)-4=16 \\ 5 &=5(5)-4=21 \end{aligned}
So, the first 5 terms are 1, 6, 11, 16, and 21
b) Every term in this sequence is generated when an integer value of n is substituted into 5n-4.
If we set 108 to equal 5n-4, we can determine if it is a part of the sequence or not. If the value of n is a whole number then it is part of the sequence, hence
5n-4=108
making n the subject by adding 4 then dividing by 5,
n=\dfrac{112}{5}=22.4
As there is no “22.4^{th}” position in the sequence, it must the case that 108 is not a term in this sequence.
Question 3: The first 5 terms of an arithmetic progression are
-3,\,\,2,\,\,7,\,\,12,\,\,17
Find the formula for the n^{th} term of this sequence.
[2 marks]
We are told it is an arithmetic progression and so must have n^{th} formula: an+b. To find a, we must inspect the difference between each term which is 5, hence a=5.
Then, to find b, let’s consider the sequence generated by 5n:
5,\,\,10,\,\,15,\,\,20,\,\,25
Every term is this sequence is bigger than the corresponding terms in the original sequence by 8. So, to get to the original sequence, we will have to subtract 8 from every term in this sequence. In other words, the n^{th} term formula for our sequence in question is
5n-8






