Speed Distance Time
Speed Distance Time Revision
Speed Distance Time
Speed is a measure of how quickly something moves, so it is calculated by dividing distance by time.
Make sure you are happy with the following topics before continuing.
Speed Distance Time – Formula
Speed, distance and time are all related by the formula,
s = \dfrac{d}{t}
where s is speed, d is distance, and t is time. You can rearrange this formula to find the other two, for example, if we multiply both sides by t and divide both sides by s, we get,
t = \dfrac{d}{s}
So, we can calculate the time by dividing the distance by the speed.
Typically, we measure distance in metres (m), kilometres (km), or miles, and we measure time in seconds (s), minutes (mins) or hours (h). As a result, the units we use to measure speed are compound units e.g m/s or km/h.
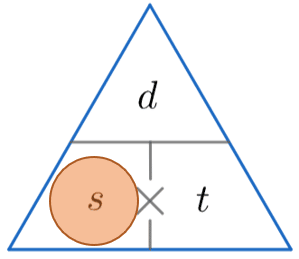
Speed Distance Time – Formula Triangle
A handy way of remembering how to calculate one of speed, distance and time is to use one of the triangles below.
The horizontal line means divide and the \times symbol means multiply.
We then cover up the one we want to find (represented by a red circle) and complete the calculation using the other two values from the triangle.
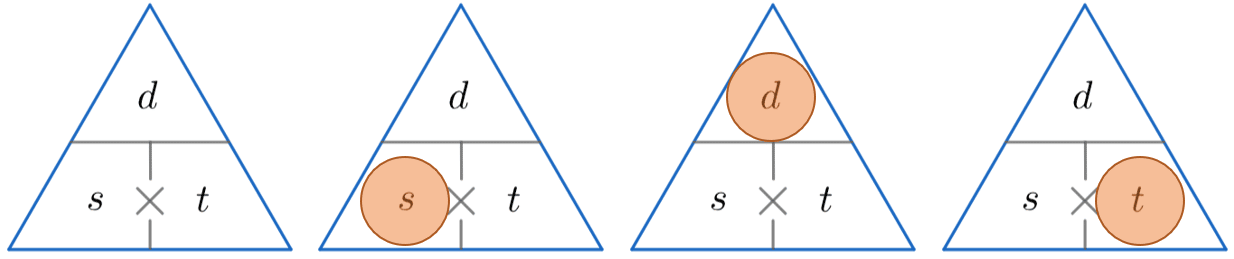
s = \dfrac{d}{t} \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, d = s \times t \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, t = \dfrac{d}{s}
Example 1: Calculating Speed
A truck travels 110 miles in 2 hours. What is the average speed of the truck?
[2 marks]
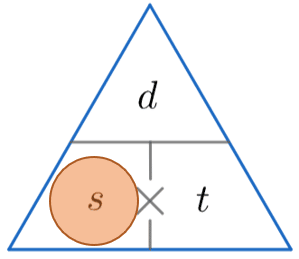

We’re looking for speed, so constructing the triangle and covering up the s, we find we must divide the distance by the time. So
\text{Speed } = 110 \div 2 = 55 mph
Example 2: Calculating Distance
Jesse throws a ball that moves at an average speed of 35 metres per second and travels for a total of 4.5 seconds. Work out the distance travelled by the ball.
[2 marks]
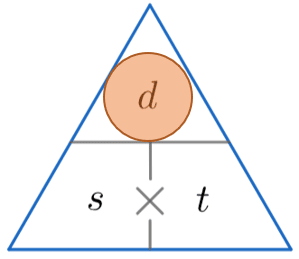

We’re looking for distance, so covering up d, we must multiply the speed by the time. So
\text{Distance }=35 \times 4.5=157.5 m
Example 3: Calculating Time
A car travels at an average speed of 50 mph. How long will it take for the car to travel 12.5 miles? Give your answer in minutes.
[2 marks]
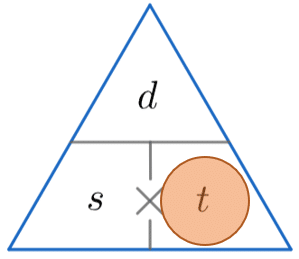

We’re looking for time, so covering t, we find we must divide the distance by the speed. So
\text{Time } = \dfrac{12.5}{50} = 0.25 hours
0.25 hours needs to be converted into minutes by multiplying by 60,
\text{Time }=0.25\times 60=15 minutes
Speed Distance Time Example Questions
Question 1: Skyler runs a new personal best in the 100-metre sprint. Her average speed over the course of the race is 8.5 metres per second. How long, to 2 decimal places, does it take her to run the race?
[2 marks]

We are calculating the time taken, so by covering up the t we can see from the triangle above that we have to divide distance, d, by speed, s.
Therefore:
\text{Time }=\dfrac{d}{s}=\dfrac{100}{8.5}=11.76 s (2 dp).
Question 2: Gustavo is driving a bus along a motorway with a speed limit of 70 miles per hour. In 30 minutes, he travels 36 miles. Is his average speed during this period exceeding the speed limit?
[2 marks]
We are calculating speed, so by covering up the s we can see from the triangle above that we have to divide distance, d, by time, t.
However, before we do that, we have to ensure that the units match. The speed limit is in ‘miles per hour’, but the time we have been given is in ‘minutes’. This is easy, as 30 minutes is half an hour, or 0.5 hours. So, Gustavo’s average speed can be calculated as follows:
\text{speed }=\dfrac{d}{t}=\dfrac{36}{0.5}=72 mph
So, yes, Gustavo is exceeding the speed limit.
Question 3: On the first part of a journey, a motorcyclist travels for 3 hours at an average speed of 55 miles per hour.
On the second part of a journey, the same motorcyclist travels for 90 minutes at an average speed of 48 miles per hour.
How far does the motorcyclist travel in total?
[4 marks]
In order to calculate the total distance travelled, we need to rearrange the speed / distance / time formula.
Since
\text{ speed} = \text{ distance} \div \text{ time}
then
\text{ distance} = \text{ speed} \times \text{ time}
The distance of the first part of the journey can be calculated as follows:
\text{Distance } = 3 hours \times \, 55 mph = 165 miles
For the second part of the journey, we need to convert the units so that they match. The speed has been given in miles per hour whereas the time has been given in minutes. We can either convert the minutes into hours or we can convert the speed form miles per hour to miles per minute. Converting minutes to hours is probably the easier option:
90 minutes = 1\frac{1}{2} hours or 1.5 hours
The distance of the second part of the journey can be calculated as follows:
\text{Distance } = 1.5 hours \times \, 48 mph = 72 miles
Therefore the total distance travelled is
165 + 72 = 237 miles
Question 4: The distance from the Sun to Mars is approximately 210 million kilometres. What is the speed of light in kilometres per second if it takes 11 minutes and 40 seconds for light to reach Mars from the Sun?
[3 marks]
We know that to calculate speed, we need to divide distance by time as per the formula:
\text{ speed} = \text{ distance} \div \text{ time}
The only issue we have in this question is that the distance has been written as ‘210 million’, which is not that helpful as ‘million’ has been written as a word and not in figures. The first thing we will need to do is convert 210 million into figures, hopefully remembering that a million has 6 zeros:
210 million = 210,000,000
The time taken has been expressed in minutes and seconds which causes an additional problem. We have been asked to give an answer in kilometres per second, so we need to convert the time from minutes and seconds to seconds.
11 minutes = 11 \times 60 seconds = 660 seconds
11 minutes and 40 seconds = 660 seconds + \, 40 seconds = 700 seconds
We are now in a position to calculate the speed of light as follows:
\text{ Speed of light} = 210,000,000 km \div \, 700 seconds = 300,000 km/s
Question 5: Voyager 1 became the first spacecraft to leave the solar system after 35 years of space travel. Given that it is travelling at a speed of 17 km/s, work out an approximation for the distance travelled. Give your answer in standard form to 3 significant figures.
[3 marks]
We know that to calculate distance, we need to multiply speed by time as per the formula:
\text{ speed} = \text{ distance} \div \text{ time}
Hence converting 35 years to seconds:
35 years =35\times365\times24\times60\times60=1.104\times10^9 seconds
The calculation becomes:
\text{ distance} = 17 \times (1.104\times10^9) =1.88\times10^{10} km






