Transformations
Transformations Revision
The Four Transformations
There are 4 types of transformation: translation, rotation, reflection, and enlargement.
You need to be able to perform each transformation as well as identify which transformations have been performed.
Type 1: Translation
Translation is the process of moving a shape.
Translations are often described using vectors,\begin{pmatrix}\textcolor{red}{x}\\\textcolor{blue}{y}\end{pmatrix}, where the top value represents the movement in x (positive means right, negative means left), and the bottom value represents the movement in y (positive means up, negative means down).
For example, the vector
\begin{pmatrix}\textcolor{red}{-3}\\\textcolor{blue}{2}\end{pmatrix}
means moving “\textcolor{red}{3} spaces left, and \textcolor{blue}{2} spaces up”. Let’s see an example.
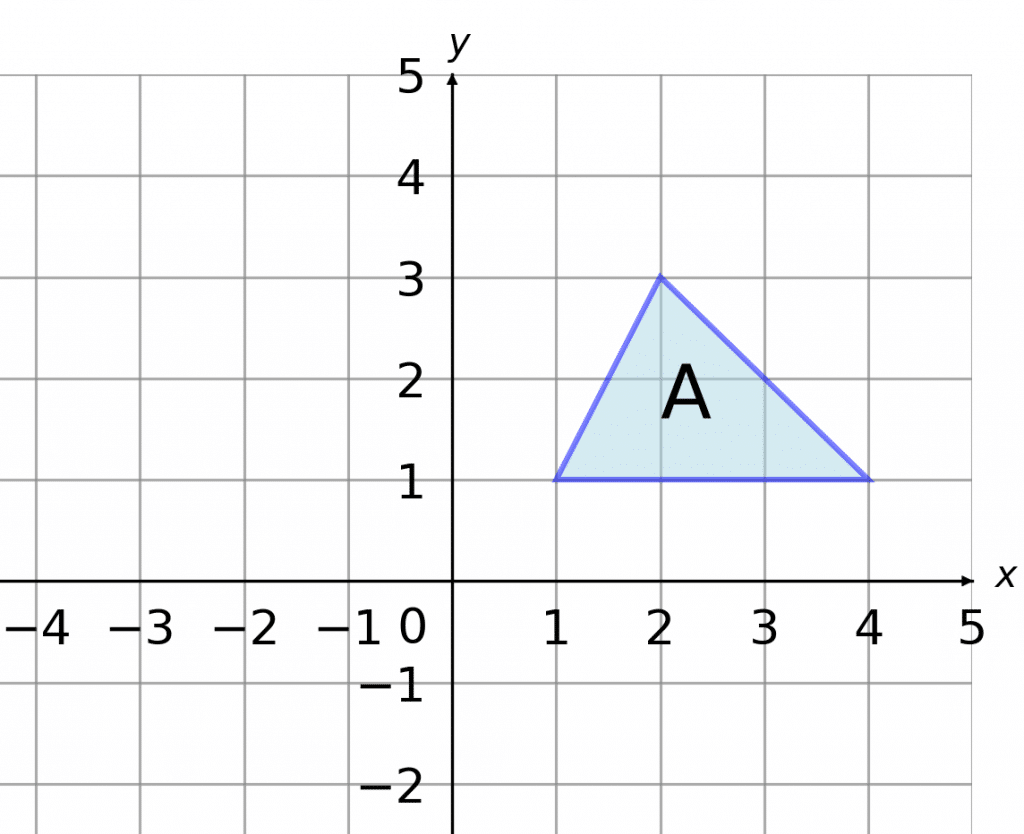

Example: Translate shape A by the vector \begin{pmatrix}\textcolor{red}{-4}\\\textcolor{blue}{1}\end{pmatrix}.
The vector in the question has a \textcolor{red}{-4} on top and a \textcolor{blue}{1} on the bottom, which means we need to translate this shape \textcolor{red}{4} spaces to the left, and \textcolor{blue}{1} space up.
One way to do this is by moving the corners one-by-one. If you shift each corner 4 spaces left and 1 space up, all that remains is to join up your new set of corners, and you get the translated shape.
The resulting shape is shown on the left.
Type 2: Rotation
The next type of transformation is rotation.
To rotate a shape or describe a rotation you need these three details:
- The centre of rotation (co-ordinates, or the origin)
- The direction you’re rotating (clockwise/anti-clockwise)
- The angle of rotation ( 90\degree, 180\degree, or 270\degree)


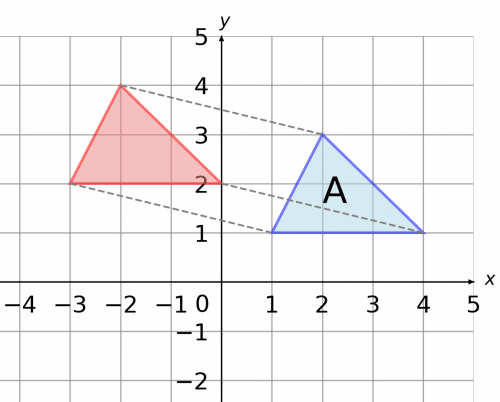
Example: Rotate shape A anti-clockwise \textcolor{blue}{90\degree} about \textcolor{orange}{(1, 1)}.
You are allowed to use tracing paper when answering these questions, and it is helpful to do so.
First mark the centre of rotation \textcolor{orange}{(1, 1)} marked with a point on the axes (red).
The direction you’re rotating, anti-clockwise means we are going to rotate in the opposite direction to the hands of a clock.
Finally, the angle of rotation, \textcolor{blue}{90\degree} is a quarter turn.
To do this on tracing paper, trace over shape A, and place your pencil on the point of rotation. Then, keep your pencil fixed, twist the paper one quarter turn anti-clockwise. The place where your traced shape ends up is the result of the rotation. The resulting shape is shown below (orange).
You may feel comfortable without tracing paper, which is great, but if you aren’t, don’t worry – you can always ask for it in an exam.
Type 3: Reflection
To reflect a shape, all you need is a mirror line (e.g x=3 or the y axis.)
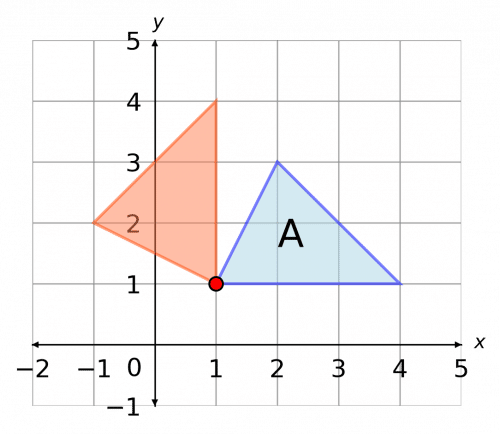
Example: Reflect shape A in the line y=0.
Firstly, recognise that the line y=0 is the x axis, and mark this on the axes (red).
This transformation can be performed with tracing paper or just by ensuring that all corners of the shape are the same distance from the mirror line.
Shape A has been reflected in the x axis to give the green shape shown.

Type 4: Enlargement
The next type of transformation is Enlargement.
To enlarge a shape or describe an enlargement you need these two details:
- The Scale factor (\text{Scale factor} = \dfrac{\text{New Length}}{\text{Old Length}})
- The centre of enlargement (co-ordinates)
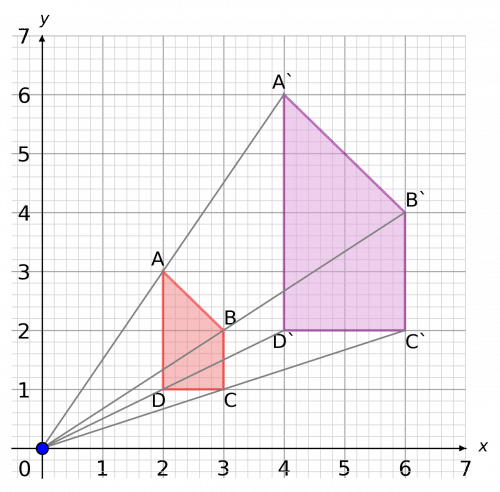
Example: Enlarge shape ABCD below by scale factor \textcolor{orange}{2} about the origin.
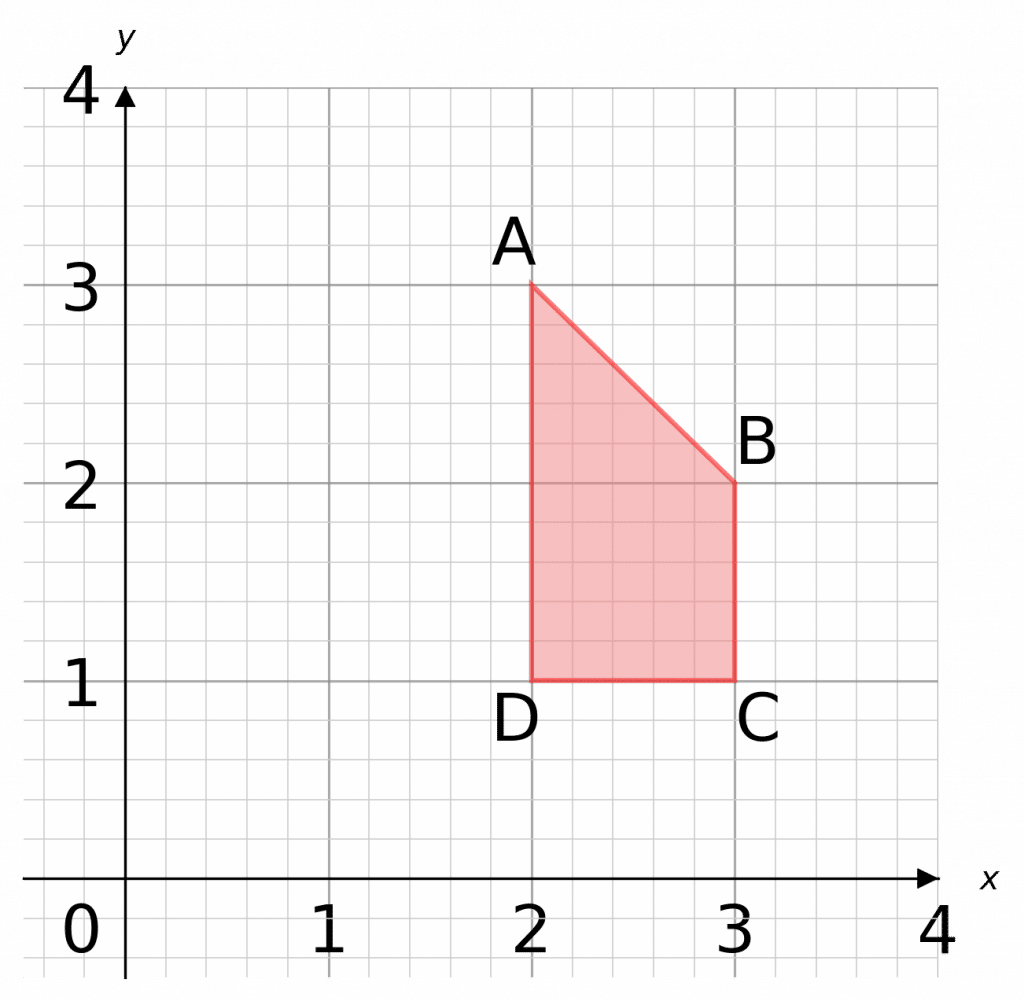

The centre of enlargement is the origin \textcolor{blue}{(0,0)}
The Scale factor is \textcolor{orange}{2}
1. First draw lines from the \textcolor{blue}{(0,0)} through all the corners of the shape. Since the scale factor is \textcolor{orange}{2}, we want to extend all of those lines to be 2 times as long (scale factor 3 would mean 3 times as long, and so on).
2. The lines are now drawn form the corners of the new shape, which is 2\times as big as the original.
AD = 2 \text{ Squares} on the original, so AD = 4\text{ Squares} on the enlarged shape.
3. Finally, join up the corners of the new shape.
As these shapes are mathematically similar, they should be the same shape.
Note: the scale factor tells you how big the shape will be, the centre of enlargement tells you where it will be.
Enlargement: Scale Factors
The key things to remember when it comes to scale factors are:
- If the scale factor is bigger than 1, the shape will get bigger and be be on the same side of the centre of enlargement
- If the scale factor is smaller than 1, the shape will get smaller and be be on the same side of the centre of enlargement
- If the scale factor is negative, the new shape will be on the opposite side of the centre of enlargement i.e. a rotation of 180\degree
Example 1: Negative enlargement
Enlarge shape A by a scale factor of -2 using (0,0) as the centre of enlargement.
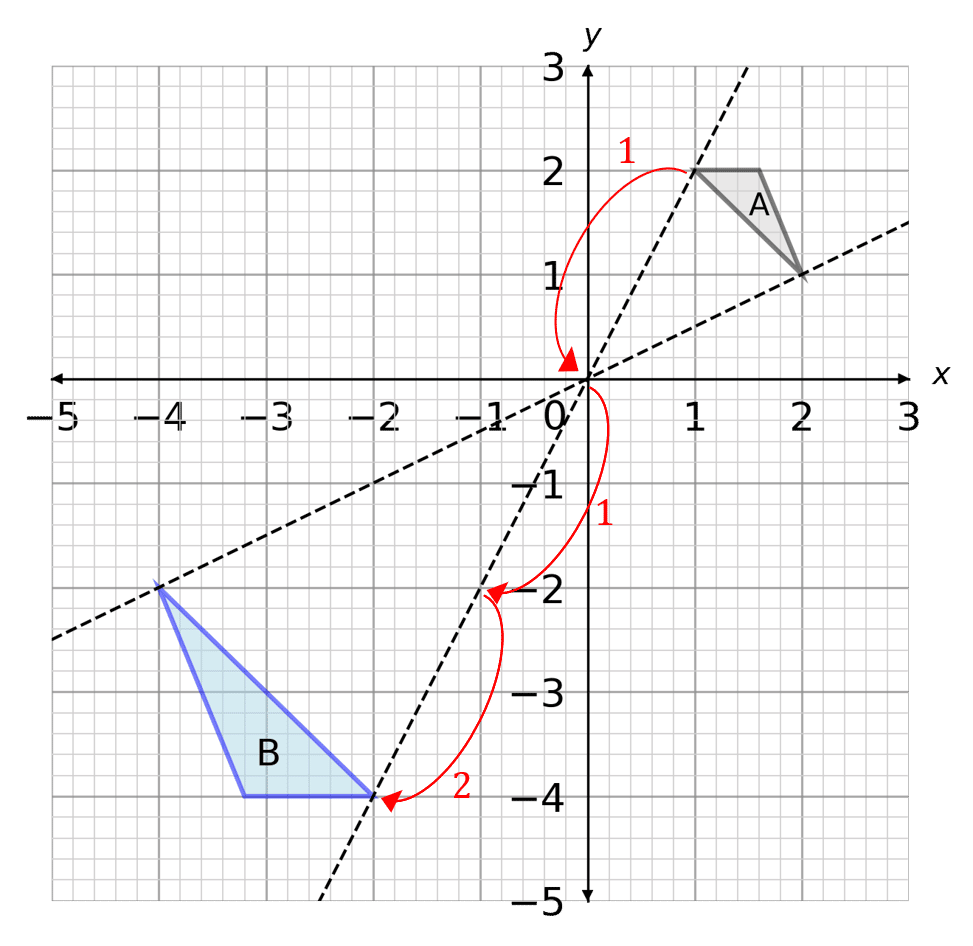

1. First draw lines from the corners of the shape through (0,0) and extending them beyond. Since the scale factor is -2, we know the shape will be on the opposite side of the centre of enlargement.
2. Multiply the distance between the corner of the shape and the centre of enlargement by 2 (since the scale factor is -2) and measure this distance on the other side, finding the corner of the new shape. Repeat for all corners of the shape
This can be seen with the red arrows on the diagram.
3. Finally, join up the corners of the new shape.
Example 2: Combinations of Transformations
The shape \text{A} on the grid below is translated by the vector \begin{pmatrix}-6\\1\end{pmatrix} then rotated 90\degree clockwise about the origin. Draw the resultant shape.

[4 marks]
First, translate the shape by the vector \begin{pmatrix}-6\\1\end{pmatrix}.

Then, rotate the shape 90\degree clockwise about the origin to get the resultant shape.

Transformations Example Questions
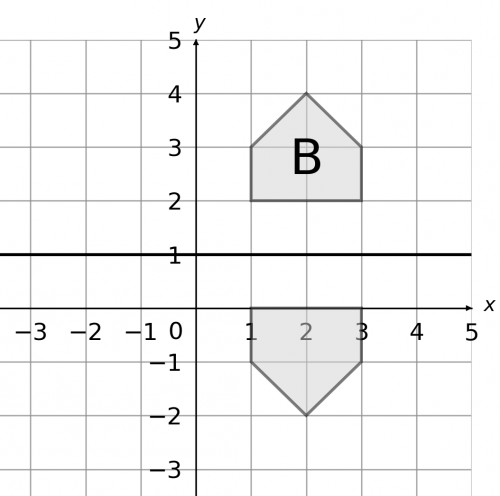
Question 1: Reflect shape B in the line y=1. Mark the resulting shape with a C.
[2 marks]
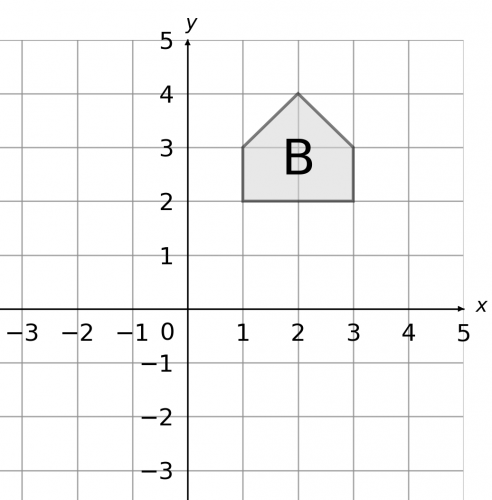
Firstly, we must draw the line y=1 onto the graph. Then, you can either choose to use tracing paper or, if you’re confident without it, just go right into the reflection.
If you’re using tracing paper, you should firstly trace over the shape and the mirror line. Then, flip over the tracing paper, and line up perfectly the mirror line on the page with the one on the tracing paper such that the trace of the shape is on the opposite side of the line to the original shape.
Then, the trace of the shape is the result of the reflection. Draw that shape onto the original axes, mark it with a C and you should get the resulting picture below.
Question 2: Describe fully the transformation that takes shape D onto shape E.
[2 marks]
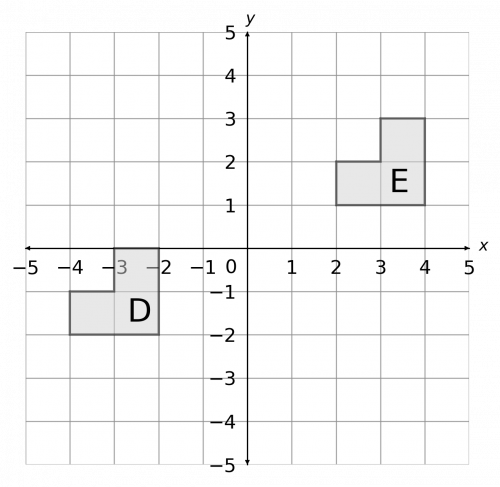
Firstly, the two shapes look the same and have the same orientation, so it wouldn’t make much sense for them to have been rotated or reflected.
Indeed, E is just the result of shifting D upwards and to the right. We must pick a corner and see how far it has moved. Looking at the bottom right corners of each shape, we can see that it has been shifted 6 spaces to the right and 3 spaces up, so the full description of the transformation is:
Translation by the vector \begin{pmatrix}6\\3\end{pmatrix}
Question 3: Enlarge shape ABC by scale factor 3 using (0, 1) as the centre of enlargement.
[3 marks]
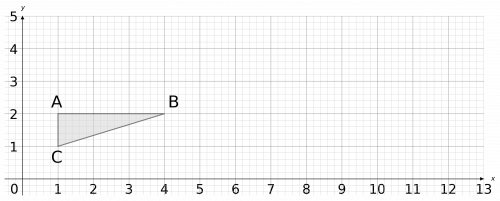
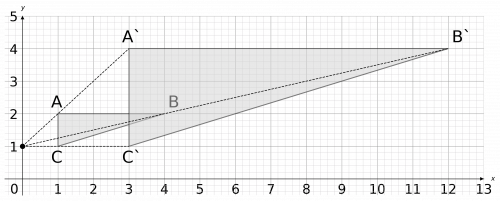
We need to draw lines from the point (0, 1) to all corners of this shape. Then, since this is an enlargement of scale factor 3, we need to extend these lines until they are 3 times longer. For example, the line from (0, 1) to A goes 1 space to the right and 1 up. So, once we’ve extended it, the resulting line should go 3 spaces to right and 3 spaces up.
Then, once all these lines have been drawn, their ends will be the corners of the enlarged shape. Joining these corners up, we get the completed shape, as seen below.
Question 4: a) Perform the following transformations to shape F in the order given.
- Rotation 180\degree about (1, 2),
- Reflection in the line y=x
Mark the resulting shape with a G.
[4 marks]
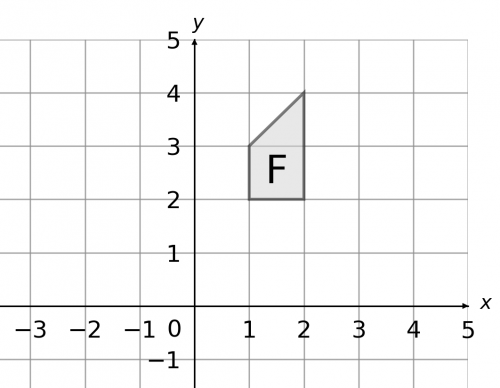
Firstly, mark the point of rotation on the axes (here, it is a red dot). Then, rotate the shape 180\degree. If you’re using tracing paper, trace the shape onto the tracing paper and place your pencil onto the rotation point. Then, twist the paper one half-turn, and where the traced shape has moved is the result of your rotation. The result of this first transformation is shown below.
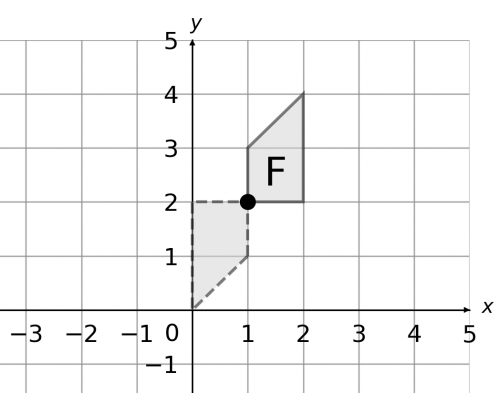
Now, we need to apply the second transformation to the result of the first one (here, the dashed grey shape).
So, we will start by drawing on the mirror line y=x (orange). Then, if you’re using tracing paper, trace both the mirror line and the shape onto the tracing paper. After that, flip the tracing paper over, and line up the mirror line on the tracing paper perfectly with the one on the paper. The location of the traced shape is the result of the reflection.
You can check it is correct by seeing if the corners of each of the shapes are the same distance from the reflection line. If you’re confident, then mark the shape G. The result is shown below.
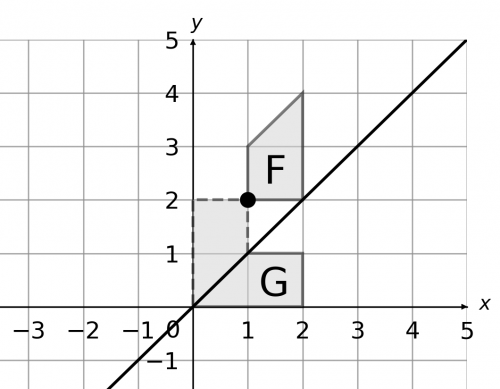
b) None of the points on F remain in the same place after being transformed onto G, so the number of invariant points is zero.
Question 5: Enlarge shape ABC by scale factor -1 about the origin.
[3 marks]
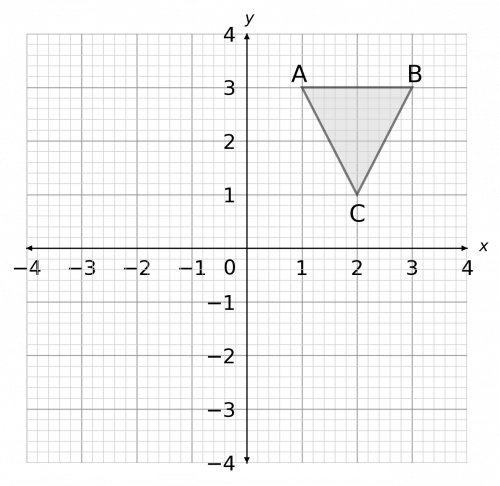
How to enlarge with a negative scale factor is a little less intuitive, but it’s not much more difficult. We still start by drawing lines from the centre of enlargement – here, the origin – to each corner of the shape. Now, rather than extending the lines outward from the corner, we extend the lines past the centre of the enlargement.
Because the scale factor is -1, the extension part of the lines (the part that goes outward from the origin, away from the shape) will be the same length as the original lines that were drawn from the corners to ABC. If the scale factor were -2, then the extension part of the lines would be twice the length of the original lines. This is subtly different to positive scale factors, so make sure you understand it.
For example, the line from the origin to C goes 2 to the right and 1 up. So, the extension to this line will, from the origin, go 2 to the left, and 1 down. Carrying this on with all the points, and then joining up the ends of the lines (since they form the corners of our shape), we get
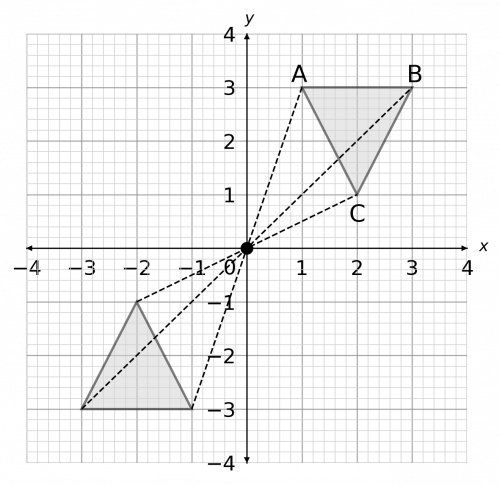
If you have a keen eye, you’ll notice this is actually equivalent to rotating the shape around the centre of enlargement by 180\degree.
Transformations Worksheet and Example Questions
(NEW) Transformations Exam Style Questions - MME
Level 1-3Level 4-5Level 6-7GCSEKS3NewOfficial MMETransformations Drill Questions
Defining Transformations - Drill Questions
Level 1-3GCSEKS3Transformations 2 - Drill Questions
Level 1-3GCSEKS3Defining Transformations 2 - Drill Questions
Level 4-5GCSEKS3Drawing Transformations - Drill Questions
Level 4-5GCSEKS3Translations - Drill Questions
Level 1-3GCSEKS3Reflections - Drill Questions
Level 1-3GCSEKS3Rotations - Drill Questions
Level 1-3GCSEKS3Enlargements - Drill Questions
Level 1-3GCSEKS3Enlargement Negative Scale Factor - Drill Questions
Level 6-7GCSE
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now





