Trigonometry
Trigonometry Revision
Trigonometry
Trigonometry is the study of triangles. In this topic, we’re going to focus on three trigonometric functions that specifically concern right-angled triangles. They are: sine, cosine, and tangent, which get shortened to sin, cos, and tan in trigonometry questions.
Make sure you are happy with the following topics before moving onto trigonometry revision.
SOHCAHTOA
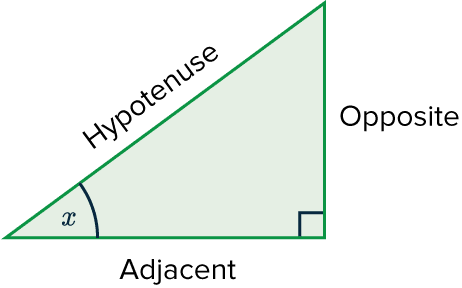
First we need to be able to label each side of a right angled triangle:
The hypotenuse is always the longest side; it is the one opposite the right-angle.
The opposite side is the side that is opposite to the angle.
The adjacent side is the side that is adjacent (next to) the angle.
\textcolor{purple}{\sin(x)}=\dfrac{\textcolor{red}{\text{opposite}}}{\textcolor{blue}{\text{hypotenuse}}}
\textcolor{purple}{\cos(x)}=\dfrac{\textcolor{limegreen}{\text{adjacent}}}{\textcolor{blue}{\text{hypotenuse}}}
\textcolor{purple}{\tan(x)}=\dfrac{\textcolor{red}{\text{opposite}}}{\textcolor{limegreen}{\text{adjacent}}}
If we let O be the opposite, A be the adjacent and H be the hypotenuse, then these are shortened to:
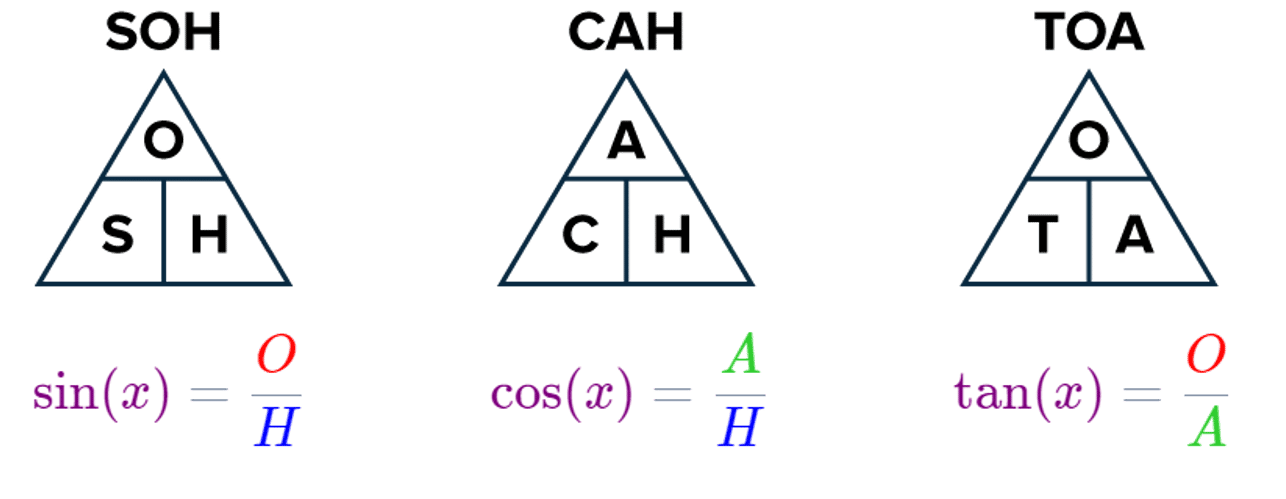
As a result, the acronym: SOHCAHTOA is helpful for remembering which sides go with which function.
Angles of Elevation and Depression
If you look towards something that is not at eye level, the angle your eyes make with the object is an angle of elevation / depression.
An angle of elevation is when you look upwards towards something.
An angle of depression is when you look downwards towards something.
These angles can be used to calculate the height and distance of objects.
Example: Bill is 30\text{ m} away from a church. The angle of elevation when he looks at the top of the church’s spire is 45\degree. If Bill’s eye level is 1.5\text{ m} above the ground, how tall is the church spire?
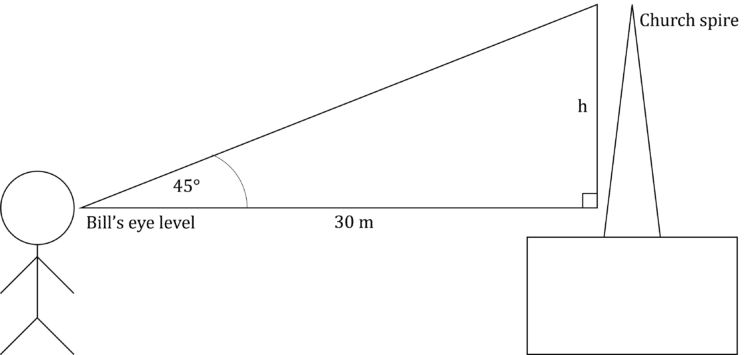
The side we want to work out is opposite from the angle we have. We also have the length of the adjacent side. This means that we want to use TOA, or \tan=\dfrac{\text{opposite}}{\text{adjacent}}
\tan(45)=\dfrac{h}{30} where h is the height we wish to calculate.
h=30\tan(45)Now, we can use \tan(45)=1 to find that h=30\text{ m}
However, this is not the height of the spire, as this was calculated from Bill’s eye level. So we have to add Bill’s eye level to this to get the real height of the spire.
\text{Height}=30+1.5=31.5\text{ m}
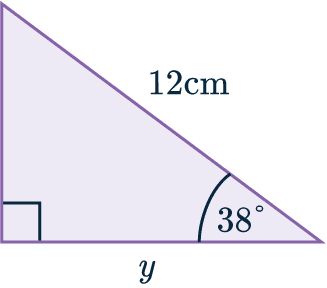
Example 1: Missing Length
Find the length of the side marked y to 1 dp.
[2 marks]
First of all we need to find which equation we need to use.
We have the hypotenuse \textcolor{blue}{H} = \textcolor{blue}{12} cm
We also have the adjacent side \textcolor{limegreen}{A} = \textcolor{limegreen}{y}
So, if \textcolor{limegreen}{A} and \textcolor{blue}{H} are the two sides we are working with, then it’s the
‘\textcolor{purple}{C}\textcolor{limegreen}{A}\textcolor{blue}{H}’ part of SOHCAHTOA we need to use.

\textcolor{purple}{\cos(x)}=\dfrac{\textcolor{limegreen}{A}}{\textcolor{blue}{H}}
Substituting in the two sides and one angle, we get:
\textcolor{purple}{\cos(38°)} =\dfrac{\textcolor{limegreen}{y}}{\textcolor{blue}{12}}
Next, we need to solve the equation. Multiplying both sides by 12 gives us:
\textcolor{limegreen}{y}=\textcolor{blue}{12} \textcolor{purple}{\cos(38°)}
Putting this into our calculator we get:
\textcolor{limegreen}{y}=9.456129043...
\textcolor{limegreen}{y}=9.5 cm (1 dp)
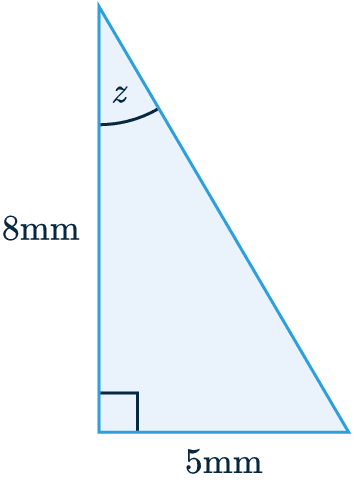
Example 2: Missing Angle
Find the size of angle z to 2 sf.
[2 marks]
First of all we need to find which equation we need to use.
We have the opposite side = \textcolor{red}{5} mm
We also have the adjacent side = \textcolor{limegreen}{8} mm
As we are working with \textcolor{red}{O} and \textcolor{limegreen}{A}, then ‘\textcolor{purple}{T}\textcolor{red}{O}\textcolor{limegreen}{A}’ is the part of SOHCAHTOA we will use:
\textcolor{purple}{\tan(z)}=\dfrac{\textcolor{red}{O}}{\textcolor{limegreen}{A}}
Substituting in the two known sides gives us:
\textcolor{purple}{\tan(z)}=\dfrac{\textcolor{red}{5}}{\textcolor{limegreen}{8}}

Now, like before we want to solve the equation to find our missing angle, z.
To solve this we need to use the inverse tan function \tan^{-1}.
What this means is that if we apply ‘\tan^{-1}‘ to both sides of the equation above, it will cancel out the tan. We get:
\textcolor{purple}{\tan(z)}=\dfrac{\textcolor{red}{5}}{\textcolor{limegreen}{8}}
z=\textcolor{purple}{\tan}^{-1}\left(\dfrac{\textcolor{red}{5}}{\textcolor{limegreen}{8}}\right)
z=32.00538321...
z=32\degree (2 sf)
This works the same way with \sin and \cos; you will need to use the \sin^{-1} and \cos^{-1}.
Example 3: Angles of Elevation and Depression
Jess looks downwards at a frisbee that has landed 4\text{ m} away from her feet. If Jess’ eye level is 1.7\text{ m} above the ground, find the angle of depression.
Give your answer to one decimal place.
[2 marks]
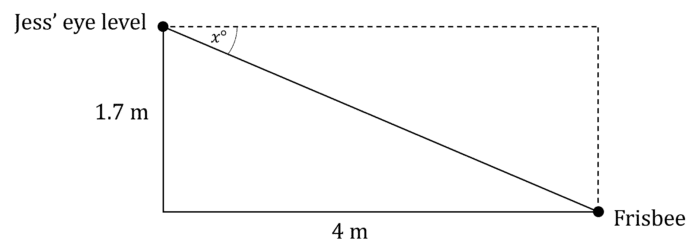
We have the opposite and adjacent side lengths of the angle we want to find, so we need to use TOA or \tan=\dfrac{\text{opposite}}{\text{adjacent}}
\tan(x)=\dfrac{1.7}{4}
x=\tan^{-1}\left(\dfrac{1.7}{4}\right)
x=23.0\degree
Trigonometry Example Questions
Question 1: Find the length of the side marked p to 3 significant figures.
[2 marks]
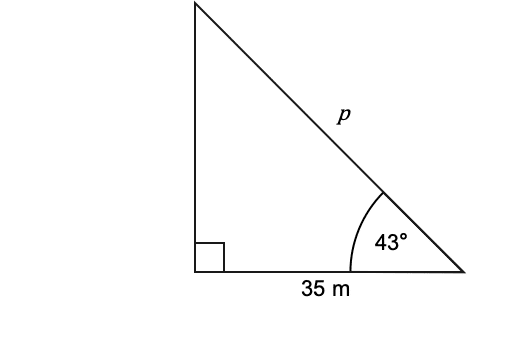
In this case, the two sides we’re concerned with are the hypotenuse and the side adjacent to the angle given. Therefore, we want the ‘CAH’ part of ‘SOH CAH TOA’ where A=35,H=p, and the angle is 43\degree:
\cos(43°)=\dfrac{35}{p}
Next we need to solve for p. Multiplying both side by p to get:
p\times\cos(43°)=35
Then, as \cos(43°) is just a number, we can we can divide both sides by \cos(43°):
p=\dfrac{35}{\cos(43°)}
Finally, putting this into the calculator we get:
p=47.85646...
p=47.9 m (3 sf)
Question 2: Find the size of the angle marked q to 1 decimal place.
[2 marks]
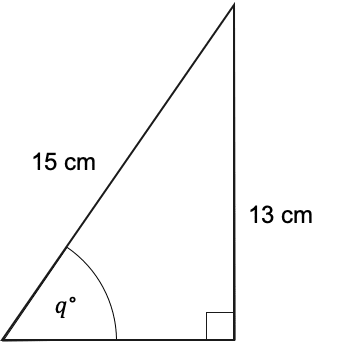
The two sides we’re working with are the hypotenuse and the opposite side, therefore, we want the ‘SOH’ part of ‘SOH CAH TOA’, where O=13,H=15, and the angle is q°:
\sin(q)=\dfrac{13}{15}
To find q, we have to apply the inverse sine function to both sides. It cancels out the sin on the left-hand side and we get:
q=\sin^{-1}\left(\dfrac{13}{15}\right)
q=60.073565...
q=60.1\degree (1 dp).
Question 3: Write down the exact value of \sin(w).
[3 marks]
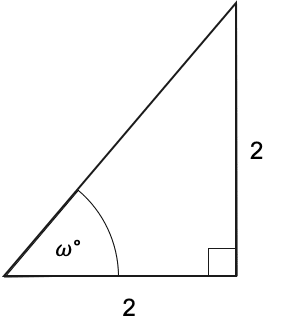
According to SOH CAH TOA, the sin of w must be equal to the opposite side divided by the hypotenuse. The opposite side is given to us: 2, but the hypotenuse is not. Since we have a right-angled triangle, we can use Pythagoras to find the hypotenuse. If the hypotenuse is c, then a and b are both 2, so the equation a^2+b^2=c^2 becomes:
c^2=2^2+2^2=4+4=8
Square rooting both sides, we get:
c=\sqrt{8}=2\sqrt{2}
Now we have the hypotenuse, we can use ‘SOH’:
\sin(w)=\dfrac{2}{2\sqrt{2}}
Notice that there is a 2 on the top and bottom that can cancel:
\sin(w)=\dfrac{2}{2\sqrt{2}}=\dfrac{1}{\sqrt{2}}
Question 4: ABC is a right angled triangle. Find the length of the side CB.
[2 marks]
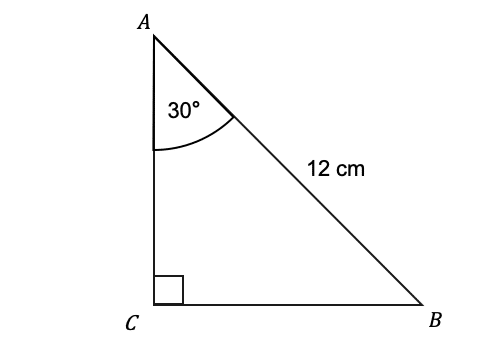
In this case, the two sides we’re working with are the hypotenuse, and the side opposite to the angle given. Therefore, we want the ‘SOH’ part of ‘SOH CAH TOA’ where O=CB,H=12, and the angle is 30\degree:
\sin(30°)=\dfrac{CB}{12}
Next we can solve this by multiplying both side by 12 to get:
12\sin(30°)=CB
Finally, putting this into the calculator we get:
CB=6.00 cm (3 sf)
Question 5: Find the size of the angle marked x to 1 decimal place.
[2 marks]
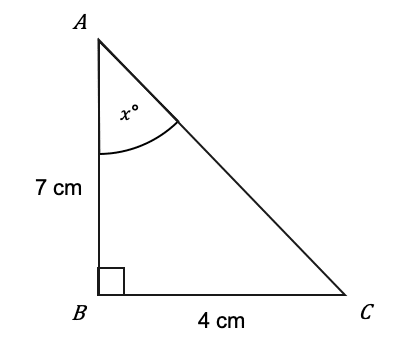
The two sides we’re working with are the adjacent and the opposite. Therefore, we want the ‘TOA’ part of ‘SOH CAH TOA’, where O=4,A=7, and the angle is x:
\tan(x)=\dfrac{4}{7}
To find x, we have to apply the inverse tangent function to both sides. It cancels out the tan on the left-hand side and we get:
x=\tan^{-1}\left(\dfrac{4}{7}\right)=29.7448813...
x=29.7° (1 dp).
Question 6: From a parking space 4\text{ m} outside a tall building, the top of the building has an angle of elevation of 87\degree. Find the height of the building. Give your answer to 1 decimal place.
[2 marks]
We have an angle of 87\degree, its adjacent of 4\text{ m} and want to find the opposite, so we need to use TOA.
\tan(87\degree)=\dfrac{h}{4} where h is the height of the building.
h=\tan(87)\times4Doing this on a calculator gives:
h=76.3\text{ m}







