Turning Points of Quadratic Graphs
Turning Points of Quadratic Graphs Revision
Turning Points of Quadratic Graphs
Graphs of quadratic functions have a vertical line of symmetry that goes through their turning point. This means that the turning point is located exactly half way between the x-axis intercepts (if there are any!).
There are two methods to find the turning point, Through factorising and completing the square.
Make sure you are happy with the following topics:
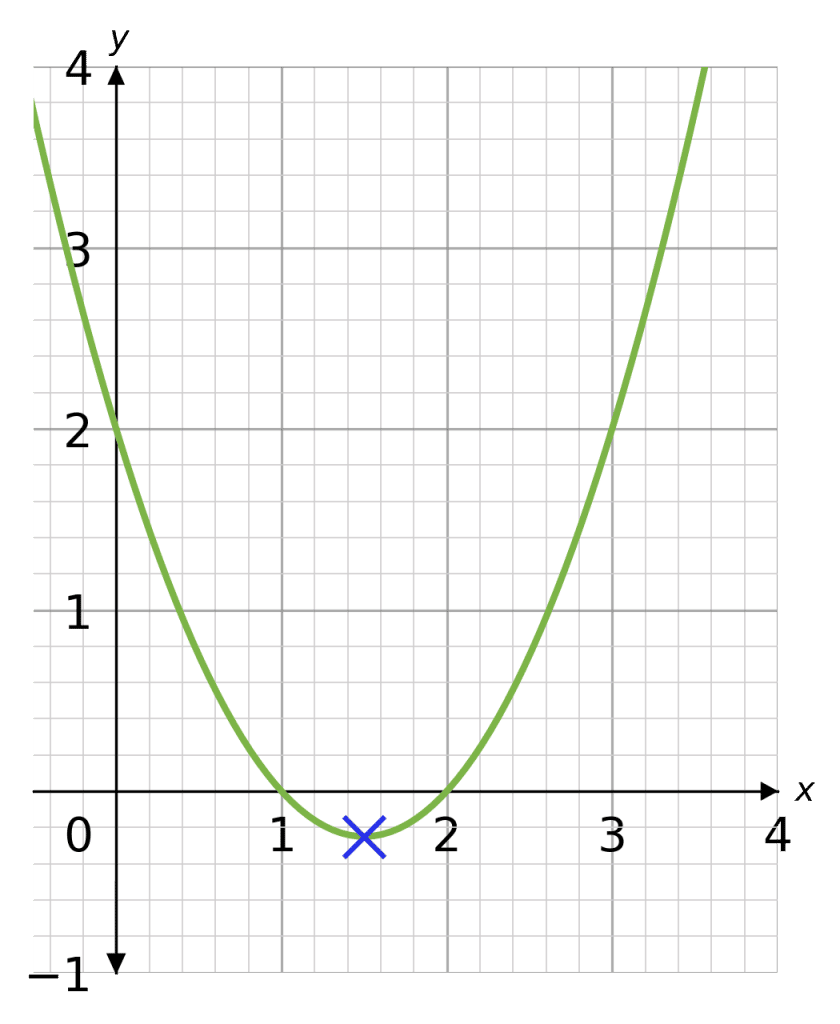
What is the Turning Point?
The turning point of a graph (marked with a blue cross on the right) is the point at which the graph “turns around”.
On a positive quadratic graph (one with a positive coefficient of x^2), the turning point is also the minimum point.
In the case of a negative quadratic (one with a negative coefficient of x^2) where the graph is upside-down, it is the maximum point.


Method 1: Through Factorising
Use the symmetry of the graph to find the coordinates of the turning point of the following quadratic:
y=x^2-3x+2
[3 marks]
Step 1: Factorise the quadratic, setting it to zero to find the locations of the roots.
Doing this we get:
x^2-3x+2=(x-1)(x-2)
Setting this equal to zero gives
(x-1)(x-2)=0
Solving we get the following roots.
x=\textcolor{red}{1} and x=\textcolor{blue}{2}
Step 2: Find the x coordinate.
We find halfway between the to x coordinates
\dfrac{\textcolor{red}{1}+\textcolor{blue}{2}}{2} = \textcolor{green}{1.5}
Therefore, the x coordinate must be \textcolor{green}{1.5}

Step 3: Find the y coordinate.
We substitute x=1.5 into the equation.
y=(\textcolor{green}{1.5})^2-3(\textcolor{green}{1.5})+2=\textcolor{orange}{-0.25}
Therefore, the coordinates of the turning point are:
(\textcolor{green}{1.5}, \textcolor{orange}{-0.25})
As you can see from the graph of the function, this answer looks correct.
Method 2: Completing the Square
Use completing the square to find the coordinates of the turning point of the following quadratic:
y=x^2+4x-12
[3 marks]
Step 1: Complete the square, this gives us the following:
y=(x+2)^2-4-12
(x\textcolor{red}{+2})^2\textcolor{blue}{-16}
This is a positive quadratic, so we are looking for a minimum point.
Step 2: Find the y coordinate of the minimum point.
The right-hand side of our equation comes in two parts. The first part, (x+2)^2, is always going to be positive no matter what x we put in, because the result of squaring a real number is always positive. If (x+2)^2 is never negative, then the smallest number it can be is zero, meaning that the minimum value of the quadratic is y=0\textcolor{blue}{-16}=\textcolor{blue}{-16}.
The y coordinate will always be equal to the \text{\textcolor{blue}{correction number}}
y = \textcolor{blue}{-16}
Step 3: Find the x coordinate of the minimum point.
The question is, what value of x must we put into our equation to make (x+2)^2=0? The answer is x=-2.
The x coordinate will equal -1 \times \text{\textcolor{red}{Number inside the bracket}}
x = -1 \times \textcolor{red}{2} = \textcolor{orange}{-2}
Therefore, the coordinates of our minimum point are:
(\textcolor{orange}{-2},\textcolor{blue}{-16})
Turning Points of Quadratic Graphs Example Questions
Question 1: Sketch the graph of y=x^2+5x+6, clearly marking on the coordinates of the roots and of the turning point.
[2 marks]
Firstly, we must find the roots of this quadratic by factorising it and setting it equal to zero. Observing that 2\times3=6 and 2+3=5, we get that
x^2+5x+6=(x+2)(x+3)
Therefore, to find the roots we set
(x+2)(x+3)=0
This clearly admits two roots: x=-2 and x=-3. Then, to find the coordinates of the turning point, we need the halfway point between the roots, which is
\dfrac{-2+(-3)}{2}=-2.5
This is the x coordinate of the turning point. To find the y coordinate, we put this value back into the equation to get
y=(-2.5)^2+5(-2.5)+6=-0.25
Then, the resulting sketch of the graph should look like
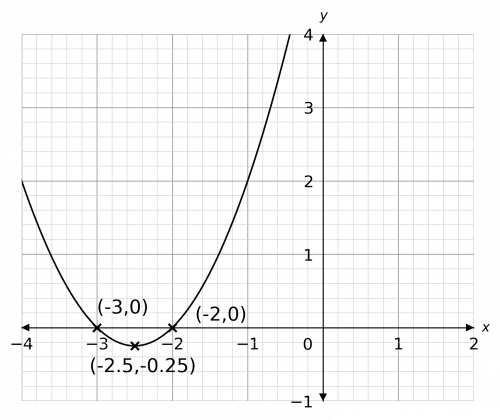
Note: Because the question asked you for a sketch, it doesn’t have to be a perfect drawing, it just has to have the correct shape and the correctly identified & labelled roots and turning points.
Question 2: Use completing the square to find the coordinates of the turning point of
y=x^2-3x+11
[2 marks]
The coefficient of x is -3, and half of -3 is -\dfrac{3}{2}. Therefore, completing the square, we get
x^2 - 3x + 11 = \left(x - \dfrac{3}{2}\right)^2 + 11 - \left(-\dfrac{3}{2}\right)^2 = \left(x - \dfrac{3}{2}\right)^2 + \dfrac{35}{4}
Thus, the coordinates of the minimum point are \left(\dfrac{3}{2}, \dfrac{35}{4}\right).
Question 3: Use completing the square to find the coordinates of the turning point of
y=-x^2+10x-3
[2 marks]
The difference here is that this is a negative quadratic, so the graph is going to have a maximum value rather than a minimum. In terms of completing the square, all we have to do is take a factor of -1 out of the quadratic
-x^2 + 10x - 3 = -(x^2 - 10x + 3),
and then complete the square on the inside of the bracket as normal. So, half of -10 is -5, therefore
-(x^2 - 10x + 3) = -\left[(x - 5)^2 + 3 - (-5)^2\right].
This simplifies to
-\left[(x - 5)^2 - 22\right] = -(x - 5)^2 + 22.
Here we can see why it’s a maximum point: the first part of the expression has a minus sign in front of it, meaning it is the negative of a square so must always be negative. So, the maximum exists where -(x-5)^2 is zero, which means that coordinates of the maximum point (and thus, the turning point) are (5, 22).
Question 4: Complete the square to find the coordinates of the turning point of y=2x^2+20x+14.
[2 marks]
To complete the square on this, we first take a factor of 2 out of the whole quadratic:
y=2(x^2+10x+7)
Now, we complete the square on the inside section. Half of 10 is 5, so we get
y=2\left[(x+5)^2+7-25\right]=2\left[(x+5)^2-18\right]=2(x+5)^2-36
Having the extra number in front of the bracket doesn’t actually change anything. We’re still looking for a minimum point, and the minimum value that 2(x+5)^2 can take is zero, so the minimum value of the quadratic is y=0-36=-36.
The x coordinate that is required to get this minimum value has to make the expression 2(x+5)^2 equal to zero, so it must be x=-5. Therefore, the coordinates of the turning point (minimum point) are (-5, -36).
If you aren’t sure about this, have another read of these two examples to make sense of it. Once you’ve got used to it, it just becomes a process of reading off the coordinates of the turning point once you have completed the square.
So, the main thing to remember is, when the result of completing the square is
a(x+b)^2+c,
the turning point of y=a(x+b)^2+c has coordinates (-b, c).






