Revise
Conversions
Conversions Revision
Conversions
A unit is a standard measurement of a particular quantity. For example, metres and kilometres are both units for measuring distance, and seconds, minutes, and hours are all units for measuring time. You will need to be familiar with Metric and Imperial unit conversions, which are two main types of unit.
Important Note:
You will also need to know how to write different units. For example, one unit of speed is “metres per second” (written like \text{m/s} or \text{ms}^{-1}), and one unit for density is “grams per cubic metre” (written like \text{g/m}^3 or \text{gm}^{-3}). “Per” means that we divide the first unit by the second.
These kinds of units that contain more than one type of unit are called compound units.
Metric and Imperial Unit Conversions
The tables below show some common Metric and Imperial unit conversions. You only need to memorise the Metric conversions. For GCSE Maths, all Imperial or Metric-Imperial conversions will be given.
Metric and Imperial Unit Conversions
The tables below show some common Metric and Imperial unit conversions. You only need to memorise the Metric conversions. For GCSE Maths, all Imperial or Metric-Imperial conversions will be given.
Converting Units – Metric and Money
When converting Metric units, all we need to do is multiply or divide similar units by a scale factor.
Example: Converting from \text{kg} to \text{g} and vice versa.
4\text{kg} = 4 \times 1000\text{g} = 4000\text{g}
4000\text{g} = 4000\text{g} \div 1000\text{g} = 4\text{kg}
Example: Converting money for example Pounds (£) to pence (p) and vice versa
£4 = 4 \times 100 = 400p
400p = 400 \div 100 = £4
These are as simple as conversions go, we will see that conversions can get a lot harder.
Converting Units – Time and Speed
Time conversions are harder than what we have previously seen. Time units are not in multiples of 10 or 1000 etc, so we have to think a bit more.
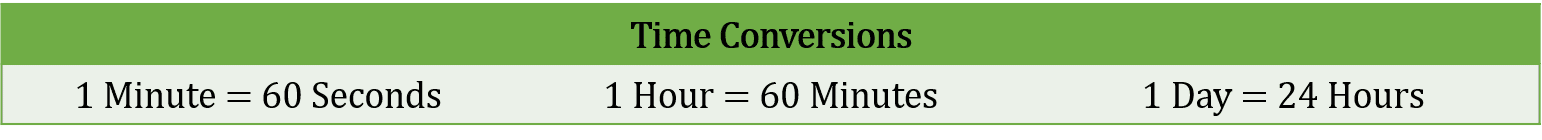
Speed conversions are some of the most difficult conversions you will see. This is because they are made up of two different measures. We have to convert the distance units and time units one at a time.
Example: A car is driving at \textcolor{red}{50} \text{km/h}. Give the speed of the car in metres per second.
Step 1: Convert the distance
1 \, \text{km} = 1000 \, \text{m}
\textcolor{red}{50} \, \text{km}= 50 \times 1000 = \textcolor{blue}{50000}\, \text{m}
So, the speed of the car is 50000 metres per hour.
Step 2: Convert the Time
1 \, \text{minute} = 60 \, \text{seconds}
1 \, \text{hour} = 60 \, \text{minutes}
1 \, \text{hour} = 60 \times 60 = \textcolor{limegreen}{3600} \, \text{seconds}
Step 3: Divide Distance by time
In other words, it will take this particular car \textcolor{limegreen}{3600} seconds to travel \textcolor{blue}{50000} metres, so the number of metres they travel every second will be:
\textcolor{blue}{50000} \div \textcolor{limegreen}{3600} = \textcolor{orange}{13.9} (1 dp).
Thus, the speed of the car is \textcolor{orange}{13.9} metres per second.
Converting Units – Length, Area, Volume (Metric)
From the red Metric conversions table, we can see that there are three different length unit conversions we need to know, \text{\textcolor{red}{mm}} to \text{\textcolor{blue}{cm}} to \text{\textcolor{limegreen}{m}} to \text{\textcolor{purple}{km}} and vice versa.
When converting areas from one unit to another, we need to be careful, as we are multiplying two units together.
1\text{ m}^2 = 100\text{\textcolor{blue}{ cm}} \times 100\text{\textcolor{blue}{ cm}} = 10000 \text{ cm}^2
1\text{ cm}^2 = 10\text{\textcolor{red}{ mm}} \times 10\text{\textcolor{red}{ mm}} = 100 \text{ mm}^2
Do not do this \xcancel{1\text{ m}^2 = 100\text{ cm}^2}!
Converting volumes from one unit to another is similar to areas, but now there is another multiplication involved.
1\text{ m}^3 = 100\text{\textcolor{blue}{ cm}} \times 100\text{\textcolor{blue}{ cm}} \times 100\text{\textcolor{blue}{ cm}} = 1000000 \text{ cm}^3
1\text{ cm}^3 = 10\text{\textcolor{red}{ mm}} \times 10\text{\textcolor{red}{ mm}} \times 10\text{\textcolor{red}{ mm}} = 1000 \text{ mm}^3
Example 1: Metric to Imperial Conversion
A baby is born weighing 4.2 kg. What is the mass of the baby in pounds to 3 sf?
Use the conversion rate 1 pound = 0.4536\text{ kg}.
[2 marks]
We have to convert a value from kilograms into pounds. That conversion rate tells us that to get from pounds to kilograms, we would need to multiply by 0.4536. Therefore, in order for us to convert kilograms to pounds we must do the opposite and divide by 0.4536.
\text{Mass of baby } = 4.2 \div 0.4536 = 9.26 pounds (3 sf)
Example 2: Volume Conversion
Shape A has a volume of 2.5 m^3 . What is this volume in cm^3?
[1 mark]
2.5 m^3 = 2.5 \times 1 m^3 = 2.5 \times 1000000 cm^3 = 2500000 cm^3
Conversions Example Questions
Question 1: Selina wishes to convert £500 into dollars for her holiday. There is a 3\% fee for converting the currency. Work out how many dollars she will have to spend on her holiday.
Use the conversion rate: \pounds 1 = \$ 1.56.
[2 marks]
We can either deduct the 3\% commission from the amount in pounds at the start or from the amount in dollars at the end (it won’t make a difference); I’d recommend getting it out of the way now. A 3\% decrease means she will have 97\% of her money left over, so
\text{Money left } = \dfrac{97}{100} \times 500 = \pounds 485
If £1 is worth \$1.56 dollars, and we are converting £485, this means that we are converting 485 times the number of pounds given to us in the exchange rate. This means that she will receive 485 times the dollar figure from the exchange rate. Therefore, the number of dollars she receives is:
485 \times 1.56 = \$756.60
Question 2: Diana measures her morning walk to work to be 2.3 kilometres. What is the distance of Diana’s walk in feet, to the nearest foot?
Use the conversion rate: 1\text{ foot} = 0.3048\text{ metres}.
[2 marks]
The conversion rate is between metres and feet, so first we need to convert 2.3km into metres. We know that 1km is 1000m, so:
2.3\text{km} = 2.3 \times 1,000 \text{m} = 2,300\text{m}
If 1 foot is equal to 0.3048 metres, that means we would have to multiply a distance in feet by 0.3048 in order to get the equivalent distance in metres. So, to go from metres to feet, we will have to divide by 0.3048. This means Diana’s walk in feet is:
2,300 \text{ metres} \div 0.3048 \text{ metres}= 7,546 \text{ feet} (to nearest foot)}
Question 3: Mo’s fish tank measures 120 \text{ cm} \times 180 \text{ cm} \times 100 \text{ cm}. What is the volume of his fish tank in \text{m}^3?
[2 marks]
The volume of his fish tank in \text{cm}^3 is:
120 \text{ cm} \times 180 \text{ cm} \times 100 \text{ cm} = 2160000 \text{ cm}^3
We know that
1 \text{ m}^3 = 1000000 \text{ cm}^3
So the volume of his fish tank in \text{m}^3 is:
2160000 \div 1000000 = 2.16 \text{ m}^3
Question 4: If a half marathon is 13.1 miles, how long will it take a runner to complete the distance running at an average pace of 5 minutes and 30 seconds per kilometre? Give your answer in hours and minutes, rounding your answer to the nearest minute.
Use the conversion rate: 1 \text{ mile} = 1.61 \text{ kilometres}
[3 marks]
Since we have been given a pace in minutes per kilometre, we will need to convert the race distance of 13.1 miles into kilometres. We can convert 13.1 miles into kilometres as follows:
13.1 \text{ miles} \times 1.61 \text{ kilometres} = 21.091 \text{ kilometres}
If it takes the runner 5 minutes and 30 seconds to run one kilometre, then we simply need to multiply 21.091 kilometres by the runner’s pace. However, the pace of the runner is in mixed units, so we will need to convert it. It makes sense to keep the pace in minutes rather than convert to seconds per kilometre:
5 \text{ minutes } 30 \text{ seconds} \equiv 5.5 \text{ minutes}
(Remember that 30 seconds is \frac{1}{2} a minute = 0.5 minutes)
The total time to complete the half marathon at a pace of 5.5 minutes per kilometre is therefore:
21.091 \text{ kilometres} \times 5.5 \text{ minutes per kilometre} = 116.0005 \text{ minutes}
The question says that we can round the answer to the nearest minute, so the half marathon will take 116 minutes.
We now need to convert 116 minutes into hours and minutes:
116 \text{ minutes} \equiv 1 \text{ hour } 56 \text{ minutes}
Question 5: A businessman buys £5,000 of euros in January which he then trades back to pounds in February. To the nearest pound, what profit has the businessman made?
January exchange rate: \pounds1 = €1.16
February exchange rate: \pounds1 = €1.15
[2 marks]
If the businessman exchanges £5,000 into euros in January, we need to calculate how many euros he receives. If £1 equates to €1.16, then £5,000 can be converted as follows:
\pounds5,000 \times €1.16 = €5,800
If he trades the €5,800 back into pounds in February, we need to calculate how many pounds he will receive. The exchange rate is €1.15 to the pound, so we need to see how many times €1.15 goes into €5,800:
€5,800 \div €1.15 = \pounds5,043 (to the nearest pound).
If the businessman started with £5,000 and ended up with £5043, he has made a profit of £43.
Conversions Worksheet and Example Questions
(NEW) Conversions Exam Style Solutions - MME
Level 4-5GCSENewOfficial MME
(NEW) Unit Conversions Exam Style Solutions - MME
Level 1-3GCSENewOfficial MMEConversions Drill Questions
