Upper and Lower Bounds
Upper and Lower Bounds Revision
Upper and Lower Bounds
Upper and lower bounds are the upper and lower values that a number can have as a result of rounding or approximating that number. There are 3 key skills that you need for upper and lower bound questions.
Make sure you are happy with the following topics before continuing.
Skill 1: Error Interval
Upper and lower bounds can also be represented as an error interval which is often given as an inequality.
Example: 57.7 has been rounded to 1 decimal place. Work out the upper and lower bounds (or error interval) of this value.
To calculate the upper and lower bound we need to use the size of the interval which is 1 decimal place (0.1).
Next we need to divide the size of the interval by 2 to get half the interval:
\dfrac{0.1}{2} = \textcolor{red}{0.05}
Step 1: Calculate the lower bound.
For the lower bound, we subtract half the interval.
Lower bound = 57.7 - 0.05 = 57.65
Step 2: Calculate the upper bound.
For the upper bound, we add half the interval.
Upper bound = 57.7 + 0.05 = 57.75
So, we express our error interval for x like
57.65 \leq x < 57.75
Note: Whilst 57.65 is included in the interval because it rounds up to 57.7, 57.75 is not included because it does not round down to 57.7. This will always be the case in an error interval.
Skill 2: Maximum and Minimum Values of a Calculation
When we do a calculation using rounded numbers, there will be a difference between the calculated value and the actual value. We use the upper and lower bounds to find the maximum and minimum values the calculation can be.
Example: A field is measured to be 34m long and 28m wide, to the nearest metre. Calculate the minimum and maximum values for the area of the field.
Step 1: Find the upper and lower bounds (error interval) for the length and width:
33.5 \leq \text{length} < 34.5
27.5 \leq \text{width} < 28.5
Step 2: Find the minimum area, by multiplying the lower bounds for length and width:
\text{Minimum Area} = 33.5 \times 27.5 = 921.25 m^2
Find the maximum area, by multiplying the upper bounds for length and width:
\text{Minimum Area} = 34.5 \times 28.5 = 983.25 m^2
So, our error interval for the area of the field is
921.25 m^2 \leq \text{Area } < 983.25 m^2
Skill 3: Truncation
When you truncate a number it is effectively always rounded down, so if a number is truncated to a certain unit, the actual value of the number can be up to a whole unit bigger than the truncated number, but no smaller. Truncating is just chopping part of the number off.
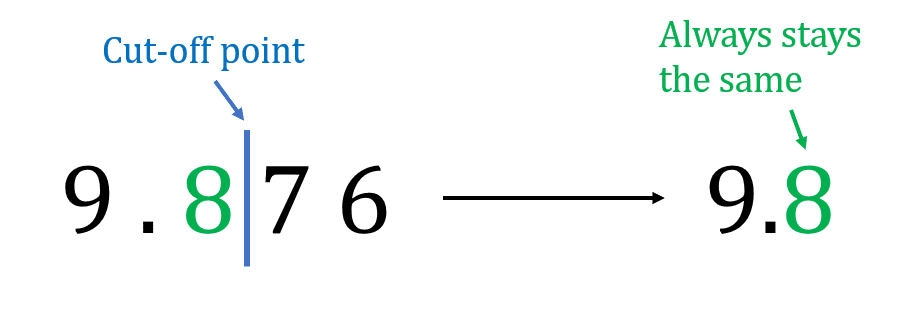
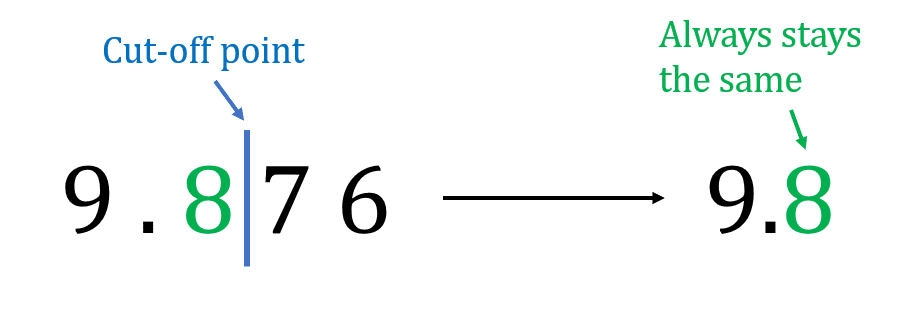
Example: What is 9.876 truncated to 1 decimal place?
Step 1: We determine our cut-off point, which is after the 1st decimal place, between the 8 and the 7.
Step 2: Any numbers after the cut-off point we ignore (chop off), and what ‘s left is our final answer. So,
9.876 truncated to 1 decimal place is 9.8
Example 1: Maximum and Minimum
A motorbike travels a distance of 110m to the nearest 10 metres, in a time of 5 seconds to the nearest second. Calculate the maximum and minimum values for the speed, s, in metres per second (m/s), using the formula
s = \dfrac{d}{t}
where d is the distance and t is the time.
[4 marks]
The error intervals for the distance and time are:
105 \leq \text{distance} < 115
4.5 \leq \text{time} < 5.5
The minimum speed is found by dividing the lower bound for the distance by the upper bound for the time. So
\text{Minimum Speed} = \dfrac{105}{5.5} = 19.0909... m/s
The maximum speed is found by dividing the upper bound for the distance by the lower bound for time. So
\text{Maximum Speed} = \dfrac{115}{4.5} = 25.555... m/s
So the error interval for the speed of the motorbike is
19.0909... m/s \leq \text{Speed} < 25.555... m/s
Example 2: Truncation
The weight of a dog has been truncated to 402.3 ounces to 1dp. Work out the interval within which w, the weight of the dog, lies.
[1 mark]
In order for some number to be truncated to 402.3, it must have began 402.3 followed by some other digits. Maybe 402.31, 402.395, 402.35467, and so on. As long as the number begins “402.3” then we’re fine.
In other words, anything that is greater than or equal to 402.3 but less than 402.4. We express this error interval like
402.3 \leq w < 402.4
Upper and Lower Bounds Example Questions
Question 1: The capacity of a jug, C, has been measured to be 5.43 litres to 2 decimal places.
Work out the interval within which C, the capacity of the jug, lies.
[1 mark]
First, consider the lower bound.
In order for the capacity of the jug to be measured as 5.43 litres to 2 decimal places, the lower bound must be greater than or equal to 5.425 litres. Any lower and it would’ve rounded down to 5.42 litres.
Next, the upper bound.
In order to round down to 5.43, the capacity of the jug must have been strictly less than 5.435. Any value which was equal to 5.435 or higher and it would’ve rounded up to 5.44.
Our lower bound is 5.425 and our upper bound is 5.435, so we express our answer as,
5.425 \leq C < 5.435
Question 2: Lily’s height was measured to be 175 cm to the nearest cm.
Work out the interval within which, Lily’s height, h, lies.
[1 mark]
The interval is determined by the bounds \pm 0.5 cm of her measured height.
We use -0.5 cm for the lower bound and +0.5 cm for the upper bound.
175-0.5=174.5
175+0.5=175.5
We can now create our interval, remembering that the lower bound has a non-strict inequality and the upper bound has a strict inequality,
174.5\leq h<175.5
Question 3: The cost of a government scheme is projected to be £5.45 billion, rounded to 2 decimal places.
Find the interval within which the cost, C, of this scheme, lies.
[1 mark]
The interval is determined by the bounds \pm £0.005 billion of the projected cost
We use -0.005 for the lower bound and +0.005 for the upper bound.
5.45 -0.005=5.445
5.45+0.005=5.455
We can now create our interval, remembering that the lower bound is a non-strict inequality and the upper bounds is a strict inequality.
£5.445 \leq C<£5.455
Question 4: A formula describing the driving force, F, in Newtons of a vehicle is given by
F = \dfrac{P}{v}
where P is the power in Watts, and v is the velocity in ms^{-1}. Given that,
P = 145 Watts to 3 significant figures
v = 23.4 ms^{-1} to 1 decimal place.
Work out the lower bound for the driving force of the car.
Give your answer to a suitable degree of accuracy.
[3 marks]
In order to make the fraction as small as possible, we want the numerator to be as a small as possible but the denominator to be as large as possible.
The lower bound for P is 144.5
The upper bound for v is 23.45
Therefore, the lower bound for the driving force of the car is,
F = \dfrac{144.5}{23.45} = 6.16 Newtons (3 sf)
This is a suitable degree of accuracy as it is the same degree to which the values are given in the question.
Question 5: The distance of a car journey is measured at 80.3 miles to 1 decimal place, whilst the time taken for the journey is 1.87 hours to 2 decimal places.
By considering both upper and lower bounds, work out the maximum and minimum average speed for this journey. Give your answer in miles per hour to a suitable degree of accuracy.
Use the formula:
\text{average speed} = \dfrac{\text{distance}}{\text{time}}
[4 marks]
To find the upper bound for the average speed, we will need the upper bound for the distance and the lower bound for the time. Whereas to find the lower bound for the average speed we will need the lower bound for the distance and the upper bound for the time.
The upper bound for distance is 80.35, whilst the lower bound is 80.25
The upper bound for time is 1.875, whilst the lower bound is 1.865.
Therefore, we get:
\text{Max average speed } = \dfrac{\text{distance upper bound}}{\text{time lower bound}} = \dfrac{80.35}{1.865} = 43.1
\text{Min average speed } = \dfrac{\text{distance lower bound}}{\text{time upper bound}} = \dfrac{80.25}{1.875} = 42.8
both to (3 sf)






