Best Buys
Best Buys Revision
Best Buys
Go to any supermarket and you’ll see all kinds of different brands selling the same product. Best buy questions require you to work out which product is the best value for money.
Make sure you are happy with the following topics before continuing.
– Ratios
Best Buys Method
For answering best buy questions, we calculate the value of each product for a common amount.
Example: Three different brands of washing powder are on sale. Their prices are shown below.
Work out which brand provides the best value for money.

In order to compare the prices of each of these brands, we will work out how much it costs to buy 100g of each brand. Then, the smallest value will tell us what the best value for money.
Brand A: The price shown is for 400g, so if we divide the value by 4, we get
\text{\textcolor{blue}{Brand A cost of 100g }}=2.56\div 4= \textcolor{blue}{\pounds 0.64}
Brand B: The price shown is for 750 g, so this time we want to divide the value by 7.5,
\text{\textcolor{red}{Brand B cost of 100g }}=5.10\div 7.5= \textcolor{red}{\pounds 0.68}
Brand C: The price shown is for 1.2 kg, which is the same as 1200 g, so we divide by 12,
\text{\textcolor{darkorange}{Brand C cost of 100g }}=7.38\div 12= \textcolor{darkorange}{\pounds 0.615}
Comparing the 3 values, we can see that the cheapest price per 100g is Brand C.
Note: Whilst you can’t actually have £0.615 (because that would involve having half a penny), it’s okay to use that value to compare prices in a best buy questions.
Example:
Two different sized cartons of milk are on sale in a shop. The smaller 300 ml carton currently has an offer that reads,
“Buy ONE get the second HALF PRICE!”
Considering this offer, work out the best value for someone looking to buying 1.5 litres of milk.
[4 marks]
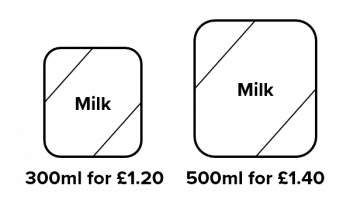
In order to get 1.5 litres, we could either get 5 small cartons or 3 large cartons.
Buying 5 smaller cartons:
For each carton, the second is half price so adding up the cost we get,
£1.20+£0.60+£1.20+£0.60+£1.20 = \textcolor{blue}{£4.80}
Buying 3 larger cartons:
£1.40+£1.40+£1.40 = \textcolor{blue}{£4.20}
This means that it is cheaper to buy 3 of the larger cartons even with the offer on the smaller ones.
Best Buys Online Exam
Best Buys Online Exam
Best Buys Example Questions
Question 1: A supermarket sells two different brands of tomato purée. Work out which brand offers better value for money.
[2 marks]
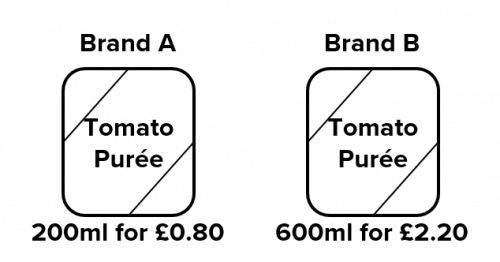
In this case, we can see that brand 2 contains 3 times as much as brand 1 (200\text{ ml} \times 3 = 600\text{ ml}), so if we calculate the cost of buying 3 containers of brand 1, that will be the same amount of tomato purée as one container of brand 2.
\text{600 ml of brand 1 costs }=\pounds0.80\times 3 = \pounds 2.40
This is more than £2.20, so we can see that brand 2 is better value for money.
Question 2: Two different brands sell boxes of pencils.
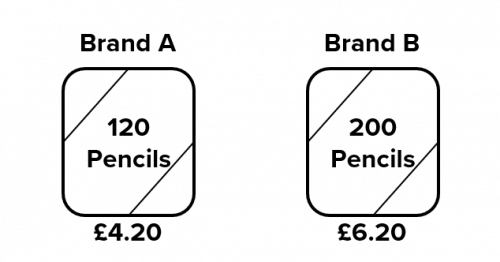
Brand A releases a new offer: “Get \bf{30}\% more pencils for the SAME PRICE!”
Considering this offer, work out which brand offers better value for money.
[4 marks]
The first thing we need to calculate in this question is how many pencils you can buy from brand 1 given that their offer states you get 30% more pencils for free.
30\%\text{ of }120 = 0.3\times 120=36\text{ extra pencils}
This means that for £4.20 you receive 120+36=156 pencils instead of 120.
The next step is to calculate how much each pencil costs for each brand.
If brand 1 sells 156 pencils for £4.20, then the price per pencil would be as follows:
\pounds4.20 \div 156 = \pounds0.0269……
If brand 2 sells 200 pencils for £6.20, then the price per pencil would be as follows:
\pounds6.20 \div 200 = \pounds0.031
As a result, when we compare the two offers, brand 1 is better value for money since the price per pencil is less.
Question 3: Mr Smith pays £4.48 for 400 g of Edam cheese and buys 250 g of Gorgonzola. Gorgonzola costs £11.60 per kilogram.
a) how much does Mr Smith pay for the Gorgonzola?
[1 mark]
b) which type of cheese is better value and by how much per gram?
[3 marks]
a) If Mr Smith is buying 250g of Gorgonzola, then this is one quarter of a kilogram (1000\text{ grams} \div 250\text{ grams} = 4).
If Gorgonzola costs £11.60 per kilogram, then the cost of 250g can be calculated as follows:
\pounds11.60 \div 4 = \pounds2.90
b) In order to compare the prices of both cheeses, we need to work out how much each cheese costs per gram.
The price of Edam can be calculated as follows:
\pounds4.48 \div 400 = \pounds0.0112 \text{ per gram}
The price of Gorgonzola can be calculated as follows:
\pounds11.60 \div1000= \pounds0.0116\text{ per gram}
As a result, we can see that the Edam cheese is better value as it costs less.
To work out the difference per gram, it might be easier to change the prices in pounds per gram to prices in pence per gram.
\text{ Edam:}\pounds0.0112 \times 100 = 1.12\text{ pence per gram}
\text{ Gorgonzola:}\pounds0.0116 \times 100 = 1.16\text{ pence per gram}
The difference between one gram of Edam and one gram of Gorgonzola can be calculated as follows:
1.16 - 1.12 = 0.04 \text{ pence per gram}
Question 4: Gary is looking for the most cost-effective taxi service in Leeds, and is trying to decide between the following 3 taxi firms:

Order the 3 firms from best value to least value for an 11 mile journey.
[4 marks]
An 11 mile journey with Swift Cabs is the trickiest of the three firms to calculate since the first mile is more expensive. Therefore, the first mile is £3.80 and the remaining 10 miles are charged at £1.60. The total cost of the journey can be calculated as follows:
\pounds3.00 + \pounds 3.80 + (\pounds1.60 \times 10) = \pounds22.80
An 11 mile journey with Zoom Taxis can be calculated as follows:
\pounds3.80 + (11 \times \pounds1.60) = \pounds21.40
An 11 mile with journey with Relaxi Cabs can be calculated as follows:
11 \times \pounds2.10 = \pounds23.10
The best value company is Zoom Taxis, the next best value is Swift Cabs, and the worst value is Relaxi Cabs.
Best Buys Worksheet and Example Questions
(NEW) Best Buys Exam Style Questions - MME
Level 4-5GCSENewOfficial MME
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now





