Symmetry
Symmetry Revision
Symmetry
Some 2D shapes have lines of symmetry and rotational symmetry.
Line of symmetry – This is a line that you can draw through a shape such that what you see on one side of that line is a “mirror-image” of what you see on the other side.
Rotational symmetry – The order of rotational symmetry of a shape is the number of times the shape can be rotated and still look the same.
You should be happy with the following topics before vising symmetry:
– 2D Shapes and Quadrilaterals
Lines of Symmetry in Regular Polygons
Below are a selection of common shapes with their lines of symmetry shown as red, dashed lines.
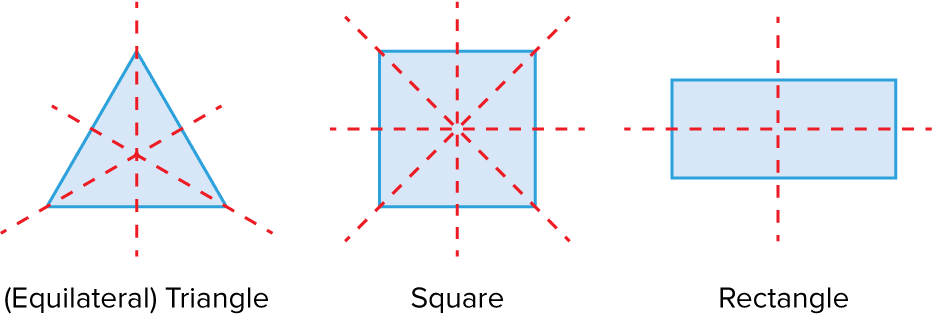
The number of lines of symmetry in a regular polygon is equal to the number of sides.
Rotational Symmetry
The order of rotational symmetry of a shape is the number of times the shape can be rotated and still look the same.
The pentagon below can be rotated 5 times and look the same.
This means it has rotational symmetry order 5.
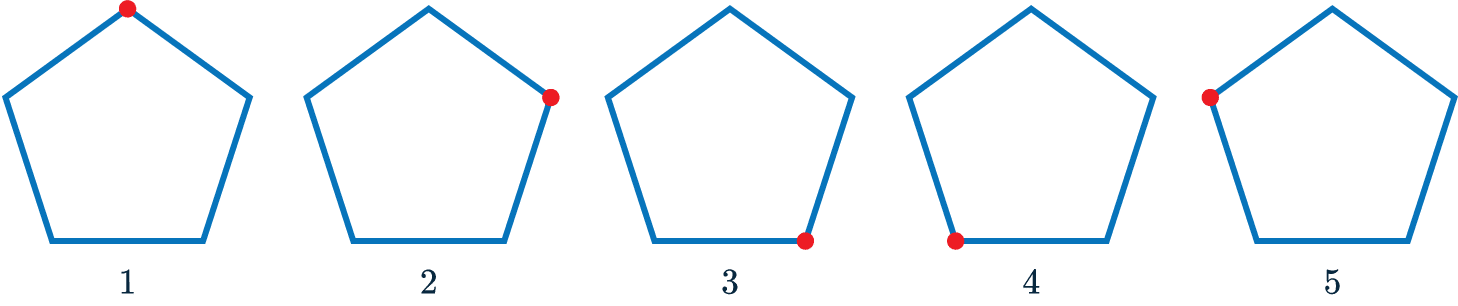
If a shape can be rotated 360\degree and only looks the same when it is back at its original position, then it has rotational symmetry order 1.
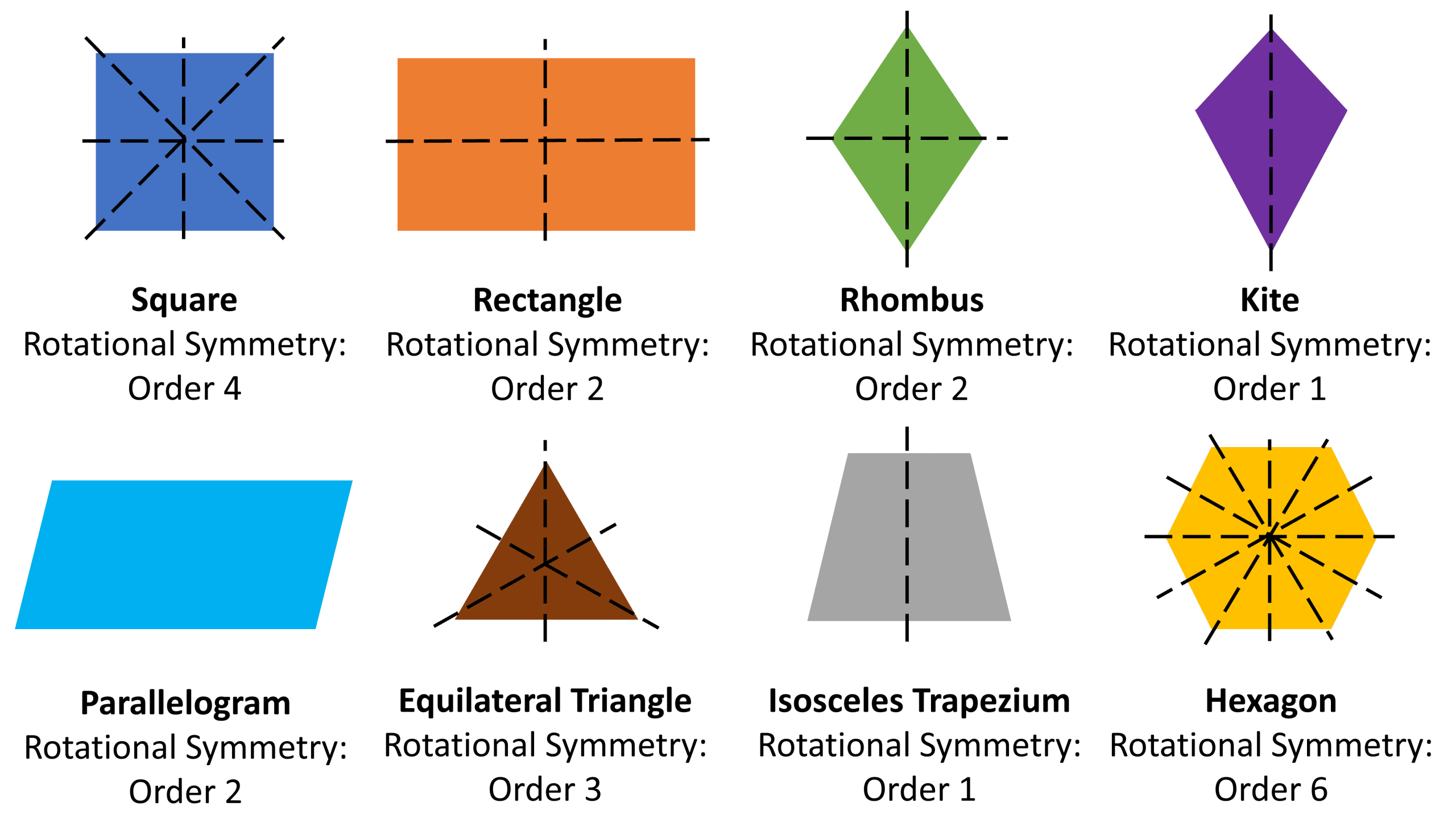
The rotational symmetry and lines of symmetry of common shapes is shown below.
Irregular polygons
Many shapes have no lines of symmetry at all, like the triangle shown below.

So, we can conclude that some triangles are symmetrical whilst others are not.
The trapezium on the left has 1 line of symmetry, whilst the trapezium on the right has none.

There’s no need to try to memorise all of these shapes and their lines of symmetry. Instead, get used to what a shape looks like when it is symmetrical.
Symmetry Example Questions
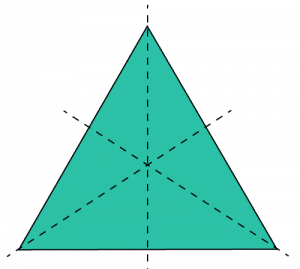
Question 1: State the number of lines of symmetry an equilateral triangle has:
[1 mark]

Looking at the picture we can see an equilateral triangle has three lines of symmetry, each one from a vertex to the centre of the opposing side,
Question 2: State the number of lines of symmetry an isosceles triangle has:
[1 mark]

Looking at the picture we can see an isosceles triangle only has one line of symmetry, a vertical line from top to bottom.

Question 3: Below is a regular pentagon. Draw all lines of symmetry on the shape
[1 mark]
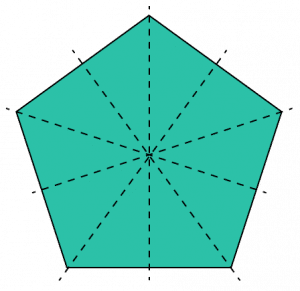
If we recall, a regular pentagon should have 5 lines of symmetry since it has 5 sides. Drawing all 5 lines on, we get the picture below:
Question 4: Draw a shape with exactly 2 lines of symmetry. Include the lines of symmetry on your drawing.
[1 mark]
There are a number of possible shapes you could make with two lines of symmetry, the most straightforward being a rectangle.

Question 5: Draw all lines of symmetry on the shape below.
[1 mark]

Symmetry Worksheet and Example Questions
(NEW) Symmetry Exam Style Questions - MME
Level 1-3GCSEKS3NewOfficial MME
MME Premium Membership
£19.99
/monthLearn an entire GCSE course for maths, English and science on the most comprehensive online learning platform. With revision explainer videos & notes, practice questions, topic tests and full mock exams for each topic on every course, it’s easy to Learn and Revise with the MME Learning Portal.
Sign Up Now





