Shop
KS3 Maths Revision Cards
KS3 Maths Revision Cards
Whether you are buying these maths cards for a year 7 student who loves maths and wants to learn more or you are getting them for a reluctant year 9 student who has an end of year exam, these cards will be useful. Our KS3 maths revision cards are effective and will help to engage your child with their maths revision. The profit from every pack is reinvested into making free content on MME, which benefits millions of learners across the country.
-
All of the major KS3 maths topics covered
-
Practice questions and answers on every topic
-
Detailed model solutions for every question
-
Great for the 23/24 school year - best rated revision cards
-
80 cards in every pack!
How the cards look
Take a look at a sample of our KS3 Maths cards below
Fast and Effective Revision
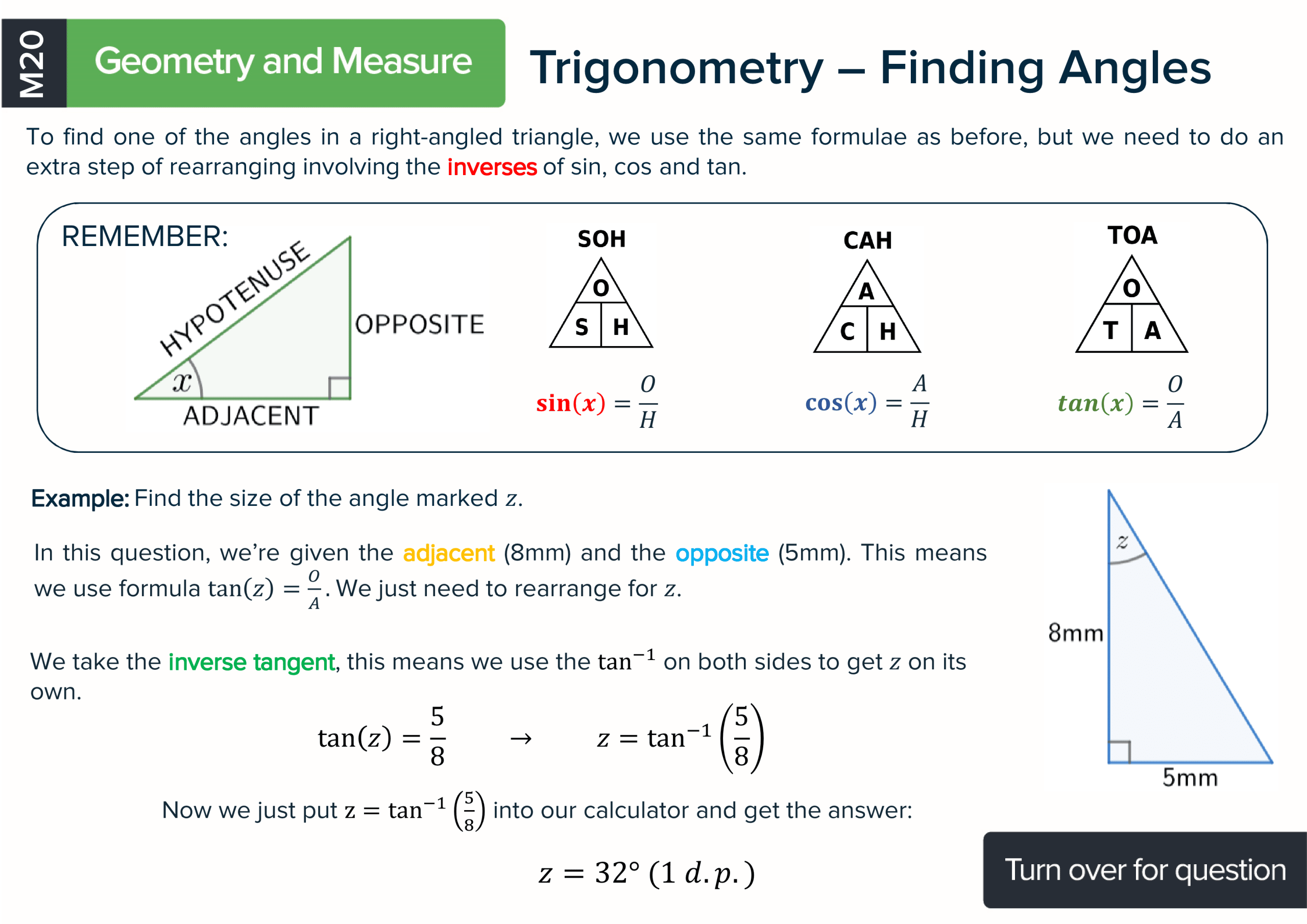
Our KS3 maths revision cards cover all the major areas of the curriculum which makes them very useful for students when trying to quickly identify areas of the course they need to revise. These flashcards not only contain explanations of each topic, they have a practise question to further test understanding. All questions are accompanied by explanations which can be easily accessed via our QR codes.
-
All major topics covered - Algebra, Number, Graphs, Ratio, Geometry, Trigonometry, Statistics and all the sub topics within the KS3 curriculum.
-
Easy to order - Press the add to cart button, add your quantity and pay, as simple as that.
-
Quick delivery - Within a few days of your order the revision cards will arrive.

Key Stage 3 Maths Flashcards
Teachers and students are always talking about flashcards being a great way to revise, and we agree. At Maths Made Easy we are the first to make a comprehensive KS3 maths revision card pack that is useful for students, teachers and even tutors. Get our KS3 maths flashcards today and start the revision revolution!
-
All abilities - Our KS3 revision cards are suitable for students of all abilities.
-
Secure payment - Either a secure card payment or Paypal, either way we don’t store your details and it is secure.

Speed Up Your Revision
The MME KS3 maths revision cards are a great way to cover the entire curriculum quickly and effectively.
Topic List
All of the topics in the KS3 maths curriculum are covered the KS3 Maths Revision Cards pack.
KS3 Maths Revision Cards
Frequently Asked Questions
Any questions you have about our KS3 Maths Revision Cards are answered here.
Yes, our KS3 maths revision cards cover the core curriculum with every major topic type covered.
These key stage three maths cards are A5, with one side dedicated to covering the key content and the reverse used for practice questions.
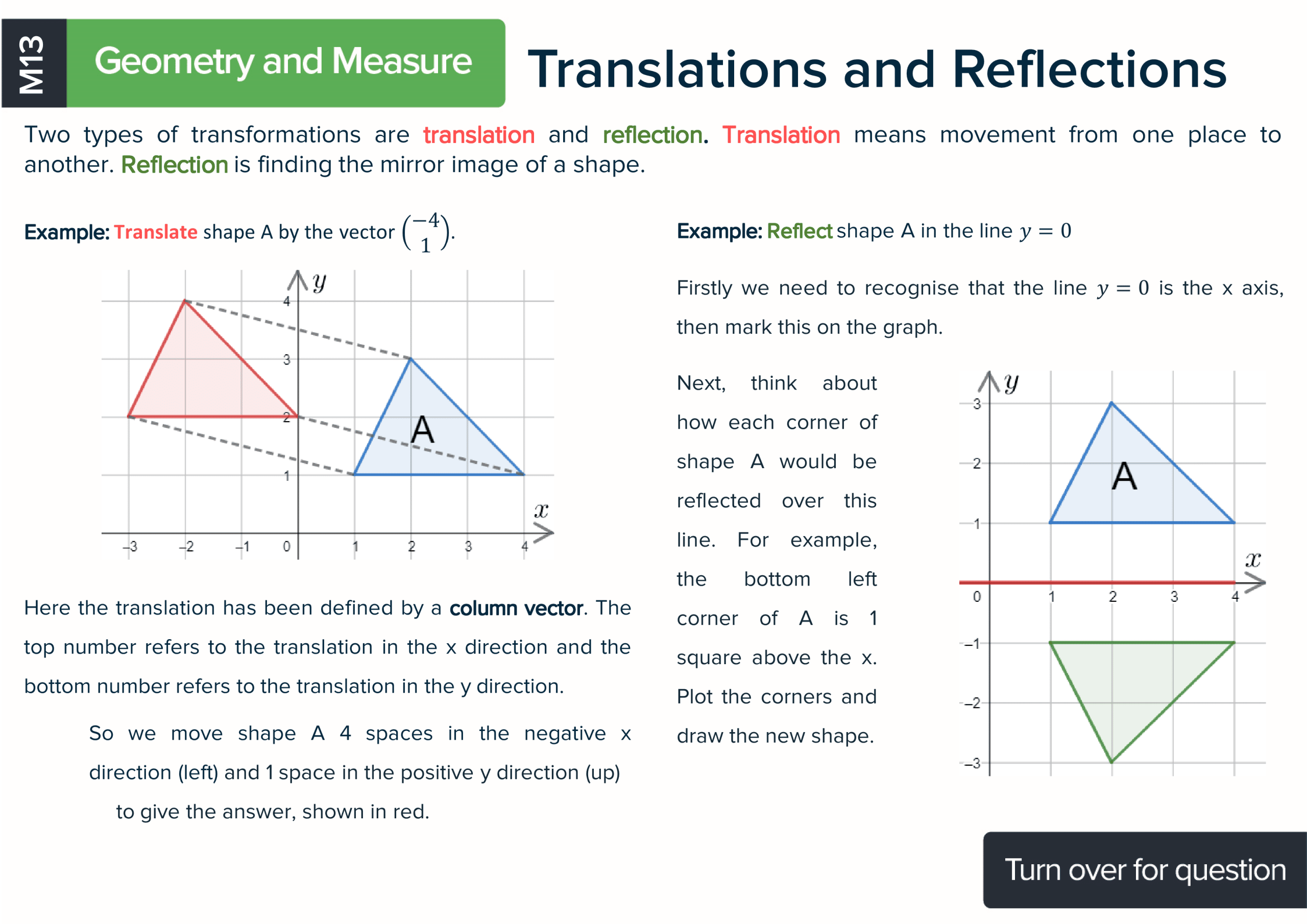
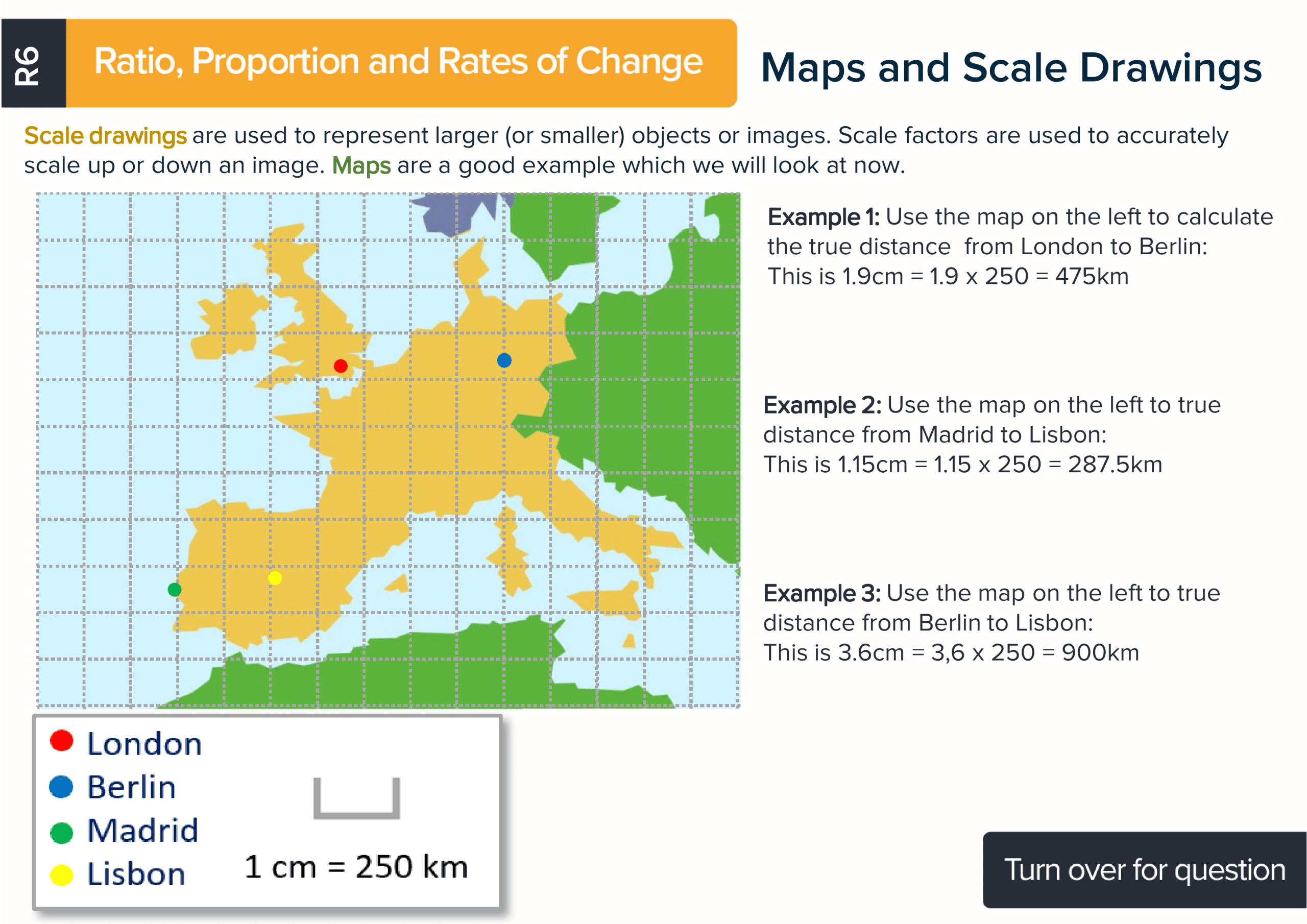
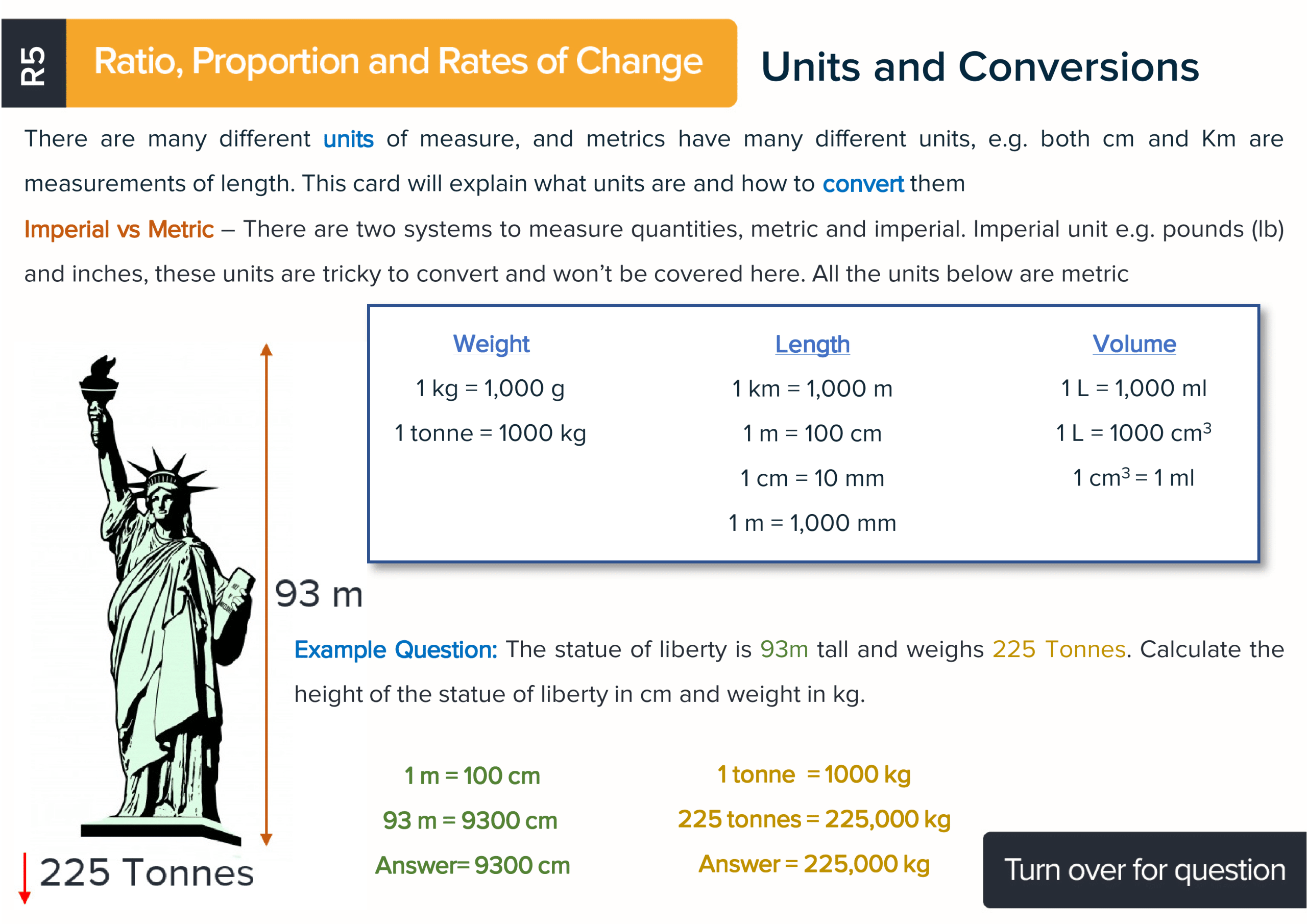
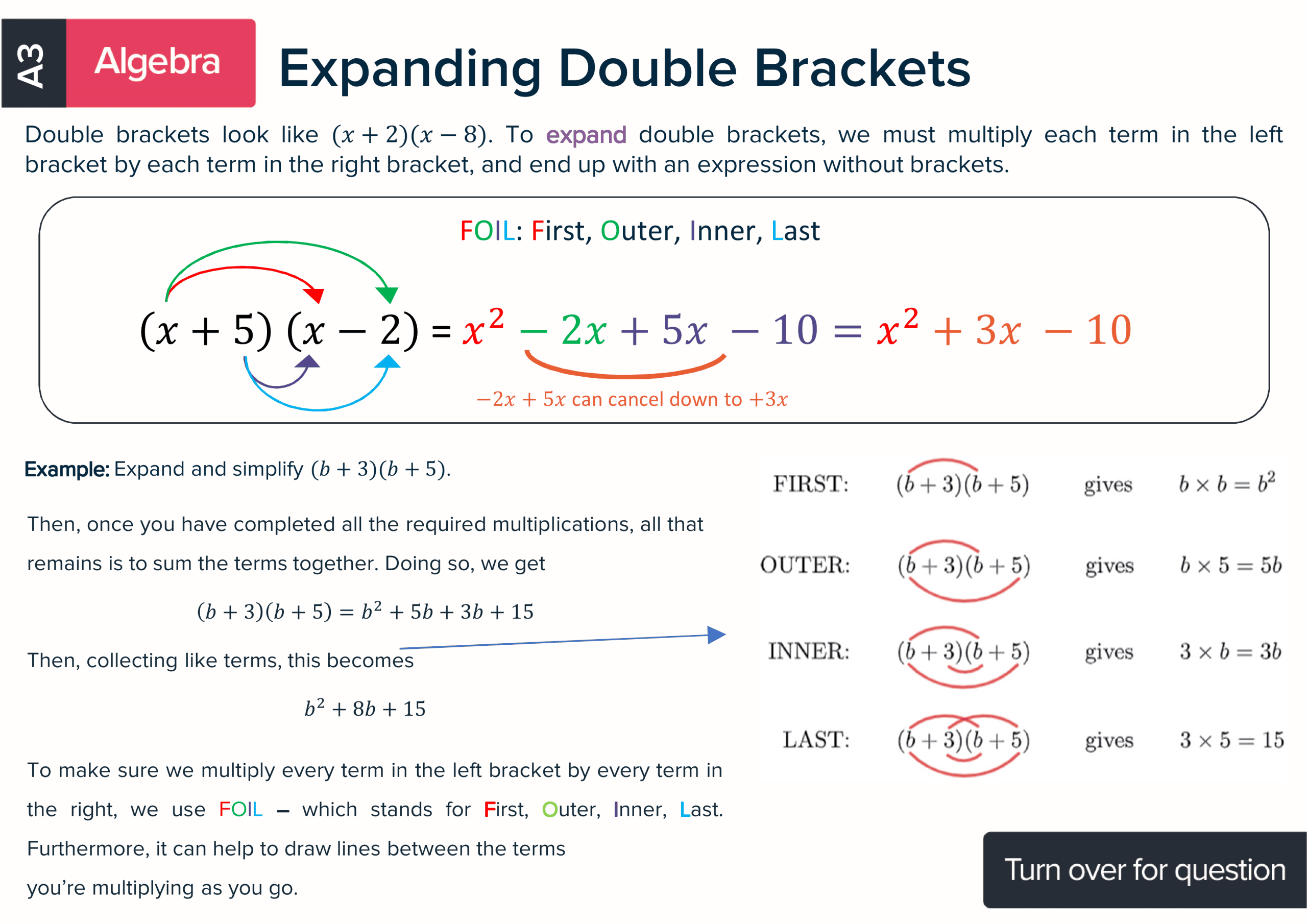
Each maths revision card has a title of the topic covered, an explanation, a formula if there is one and at least one worked example so students can learn how to answer questions using the best methods. There is also a question on the reverse of every card with space for working. Each card has a QR code to make accessing the answers and further KS3 revision materials as easy as possible.
We use Royal Mail to ship all KS3 card orders. This usually takes 2-3 days for our standard shipping option.
We offer discounts for larger orders which are typically placed by schools and tuition agencies. Our order form takes care of all discount codes and bulk order discounts which are applied automatically to the basket.
You can scan the handy QR code which will take you directly to the worked solution as well as tonnes of other relevant KS3 revision materials. If you have an iPhone you can simply scan the code with your camera, for Android phones there are tonnes of free QR apps. Alternatively you can use the code on the card to access the correct answers directly through the site.
KS3 Maths Revision Card Answers
Get the answers for the KS3 Maths Revision Cards here.

Shipping / Delivery Information
All items are shipped using Royal Mail. For our standard shipping option, this means you should receive your items within 2-3 working days for all UK orders. International shipping varies depending on the country but usually takes between 5-10 working days.
| Item | United Kingdom | Europe | Rest of World |
|---|---|---|---|
| Orders Under £40 | Royal Mail (3-4 Working days): £1.99 Royal Mail 24 (1-2 working days): £4.99 |
Europe Shipping:£19.99 | Varies |
| Orders Over £40 | Free UK shipping (3-4 Working days) Royal Mail 24 (1-2 working days): £4.99 |
Europe Shipping:£19.99 | Varies |
Bulk Discounts for Schools
MME offers bulk discount for schools/colleges and training providers, as well as a dedicated mock paper printing service. Check out the pricing below and place an order using the order form below. Alternatively, fill in the contact form to request more information.
Price List
Order Form
Rating breakdown
-
5 stars74
-
4 stars6
-
3 stars5
-
2 stars1
-
1 stars0
Highly rated for:
of customers recommend this product
Secure Shopping at MME
All payment details you send us are shielded via SSL encryption.

Ways to Pay
We accept all major credit / debit cards, PayPal, Apple Pay & Google Pay.
Helping you buy
Having trouble? Call our customer support team:
020 3633 5145
Need it quicker?
Place your order before 2pm and select Next Working Day delivery at checkout.





















The maths cards do the job!
Nice set of maths cards and fast shipping as well
Set of cards that cover maths is not exactly exciting. Could have been more inventive with the content in my opinion.
These cards are great, simple and easy to use. D is able to use them independently, which supports and encourages confidence. Not too worried they aren’t in a nice box as if they are being used they wouldn’t be in the box and not having to get them out specifically means they are accessible to use.
Excellent for helping children to engage with maths in something a little different to a screen!
I can not pick a fault in the cards themselves as they look great and break things down into smaller more manageable chunks for our daughter to understand and it is definitely working. The only slight criticism is the packaging the cards come in could be a little more inspiring.
Excellent revision materials just poorly presented wrapped in elastic bands with slow delivery. They have clearly got the content right, just need a corporate gloss to make the cards shine.
I was sent the first set but made a mistake with my address and they were so helpful and agreed to send out another set for me. The maths cards themselves are what we had hoped for. Excellent!
Good service and delivery
Fast delivery and nice cards.